Bộ 12 đề thi học kì 2 Toán 7 Cánh Diều cấu trúc mới có đáp án - Đề 12

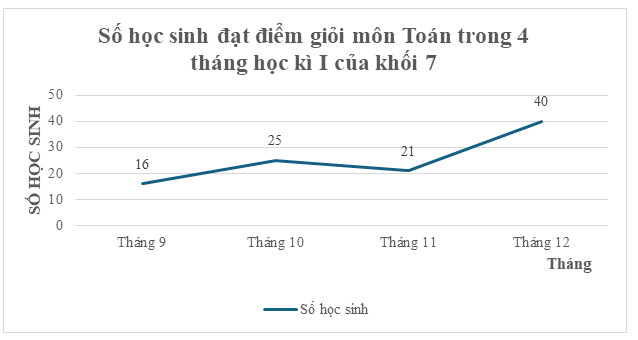
a) Bảng dữ liệu theo mẫu số liệu trên là:

b) Từ tháng 9 đến tháng 10, số học sinh đạt điểm giỏi môn Toán của khối lớp 7 tăng số học sinh là:

\(25 - 16 = 9\) (học sinh)

c) Số học sinh đạt điểm giỏi môn Toán tháng 11 so với tháng 10 là \(\frac{{21}}{{25}}.100 = 84\% \).

Do đó, số học sinh đạt điểm giỏi môn Toán tháng 11 giảm so với tháng 10 là:

\(100\%  - 84\%  = 16\% \).

a) Biến cố chắc chắn là biến cố \(M\): “Tổng các số ghi trên hai quả bóng lớn hơn 2”, vì hai số nhỏ nhất ghi trên mỗi quả bóng lấy từ hai hộp lần lượt là \(1\) và \(2\) nên tổng các số gho trên hai quả bóng nhỏ nhất là \(3\), chắc chắn lớn hơn \(2.\)

Biến cố không thể là biến cố \(P\): “Chênh lệch giữa hai số ghi trên hai quả bóng bằng 10”. Vì chênh lệch lớn nhất giữa hai số lấy được trên mỗi quả bóng từ hai hộp là 9, khi hộp \(A\) lấy được số 1 và hộp \(B\) lấy được số \(10\).

b) Trong năm quả bóng từ hộp \(A\) ghi các số \(1;3;5;7;9\) có ba số nguyên tố là \(3;5;7\).

Do đó, xác suất của biến cố \(Q\) là \(\frac{3}{5}.\)

c) Trong năm quả bóng từ hộp \(B\) ghi các số \(2;4;6;8;10\) có các số là ước của \(16\) là: \(2;4;8\).

Do đó, xác suất của biến cố \(P\) là \(\frac{3}{5}.\)

a) Diện tích của hình vuông là \(x{\rm{ }}\left( {{\rm{cm}}} \right)\) là: \({x^2}{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).

Diện tích của tam giác vuông cân có độ lớn cạnh góc vuông là \(y{\rm{ }}\left( {{\rm{cm}}} \right)\) là: \(\frac{1}{2}{y^2}{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).

Tổng diện tích của hình vuông và của tam giác vuông cân là: \({x^2} + \frac{1}{2}{y^2}{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).

b) Thay \(x = 2\) và \(y = 4\) vào biểu thức, ta có: \({x^2} + \frac{1}{2}{y^2} = {2^2} + \frac{1}{2}{.4^2} = 12{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).

Vậy tổng diện tích của hình vuông và của tam giác vuông cân khi \(x = 2\) và \(y = 4\) là \(12{\rm{ c}}{{\rm{m}}^2}.\)

a) \(A\left( x \right) = \frac{1}{4}{x^3} + \frac{{11}}{3}{x^2} - 6x - \frac{2}{3}{x^2} + \frac{7}{4}{x^3} + 2x + 3\)

            \( = \left( {\frac{1}{4} + \frac{7}{4}} \right){x^3} + \left( {\frac{{11}}{3} - \frac{2}{3}} \right){x^2} + \left( { - 6 + 2} \right)x + 3\)

            \( = 2{x^3} + 3{x^2} - 4x + 3\).

b) Đa thức \(A\left( x \right)\) có bậc là 3 và hệ số cao nhất là \(2\).

c) Ta có \(A\left( { - 1} \right) = 2.{\left( { - 1} \right)^3} + 3.{\left( { - 1} \right)^2} - 4.\left( { - 1} \right) + 3 = 8\).

Theo bài, \({2^n} = A\left( { - 1} \right)\) nên \({2^n} = 8 = {2^3}\)

Suy ra \(n = 3\).

Vậy \(n = 3\).

d) \(B\left( x \right) = \left( {{x^2} - x + 1} \right)\left( {2x + 3} \right)\)

             \( = 2{x^3} + 3{x^2} - 2{x^2} - 3x + 2x + 3\)

             \( = 2{x^3} + {x^2} - x + 3\)

Ta có \(C\left( x \right) = A\left( x \right) - B\left( x \right)\)

                       \( = 2{x^3} + 3{x^2} - 4x + 3 - \left( {2{x^3} + {x^2} - x + 3} \right)\)

                       \( = 2{x^3} + 3{x^2} - 4x + 3 - 2{x^3} - {x^2} + x - 3\)

                       \( = 2{x^2} - 3x\).

Để tìm nghiệm của đa thức \(C\left( x \right)\), ta cho \(C\left( x \right) = 0\)

Do đó \(2{x^2} - 3x = 0\) hay \(x\left( {2x - 3} \right) = 0\)

Suy ra \(x = 0\) hoặc \(x = \frac{3}{2}\).

Vậy nghiệm của đa thức \(C\left( x \right)\) là \(x \in \left\{ {0;\frac{3}{2}} \right\}\).

a) Xét \(\Delta ABD\) và \(\Delta EBD\), có:

\(\widehat {BAD} = \widehat {BED} = 90^\circ \);

\(BD\) là cạnh chung;

\(\widehat {ABD} = \widehat {EBD}\) (do \(BD\) là tia phân giác của \(\widehat B\)).

Do đó \(\Delta ABD = \Delta EBD\) (cạnh huyền – góc nhọn).

Suy ra \(BA = BE\) (hai cạnh tương ứng).