Bộ 12 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 10
22 người thi tuần này 4.6 7 K lượt thi 5 câu hỏi 45 phút
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
5 câu Trắc nghiệm Tập hợp các số hữu tỉ có đáp án (Nhận biết)
6 câu Trắc nghiệm Toán 7 Bài 3: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh có đáp án (Vận dụng)
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
8 câu Trắc nghiệm Toán 7 Bài 4: Đơn thức đồng dạng có đáp án (Nhận biết)
5 câu Trắc nghiệm Toán 7 Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu có đáp án (Nhận biết)
5 câu Trắc nghiệm Toán 7 Bài 7: Tính chất đường trung trực của một đoạn thẳng có đáp án (Nhận biết)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
1.1.
|
a) \(\frac{x}{3} = \frac{{ - 10}}{6}\) \(6x = - 10.3\) \(6x = - 30\) \(x = - 30:6\) \(x = - 5\) Vậy \(x = - 5\). |
b) \(\frac{{2 - x}}{4} = \frac{{x - 3}}{{ - 5}}\) \( - 5\left( {2 - x} \right) = 4\left( {x - 3} \right)\) \( - 10 + 5x = 4x - 12\) \(x = - 12 + 10\) \(x = - 2\) Vậy \(x = - 2\). |
1.2. Gọi số cán bộ y tế ở đội thứ nhất, đội thứ hai, đội thứ ba lần lượt là \(x,y,z\) (người) với \(x,y,z \in {\mathbb{N}^*}.\)
Vì cả ba đội y tế có tất cả 37 cán bộ y tế nên \(x + y + z = 37\).
Ta có: \(x\) tiêm xong trong 5 ngày, \(y\) tiêm xong trong 4 ngày, \(z\) tiêm xong trong 6 ngày.
Vì số cán bộ y tế và thời gian là hai đại lượng tỉ lệ nghịch nên ta có: \(5x = 4y = 6z\) hay \(\frac{x}{{12}} = \frac{y}{{15}} = \frac{z}{{10}}.\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\frac{x}{{12}} = \frac{y}{{15}} = \frac{z}{{10}} = \frac{{x + y + z}}{{12 + 15 + 10}} = \frac{{37}}{{37}} = 1\).
Do đó, ta có: \(\frac{x}{{12}} = 1\) nên \(x = 12,\) \(\frac{y}{{15}} = 1\) nên \(y = 15\); \(\frac{z}{{10}} = 1\) nên \(z = 10\).
Vậy số cán bộ y tế ở đội thứ nhất, thứ hai, thứ ba lần lượt là 12, 15, 10 người.
Lời giải
2.1. Thay \(x = - 1;y = 1;z = - 1\) vào biểu thức \(H = xy - xz + yz\), ta được:
\(H = \left( { - 1} \right).1 - \left( { - 1} \right).\left( { - 1} \right) + 1.\left( { - 1} \right) = - 1 - 1 - 1 = - 3\).
Vậy giá trị của biểu thức \(H = - 3\).
2.2. a) \(A\left( x \right) = \frac{1}{4}{x^3} + \frac{{11}}{3}{x^2} - 6x - \frac{2}{3}{x^2} + \frac{7}{4}{x^3} + 2x + 3\)
\( = \left( {\frac{1}{4} + \frac{7}{4}} \right){x^3} + \left( {\frac{{11}}{3} - \frac{2}{3}} \right){x^2} + \left( { - 6 + 2} \right)x + 3\)
\( = 2{x^3} + 3{x^2} - 4x + 3\).
b) Đa thức \(A\left( x \right)\) có bậc là 3 và hệ số cao nhất là \(2\).
c) Ta có \(A\left( { - 1} \right) = 2.{\left( { - 1} \right)^3} + 3.{\left( { - 1} \right)^2} - 4.\left( { - 1} \right) + 3 = 8\).
Theo bài, \({2^n} = A\left( { - 1} \right)\) nên \({2^n} = 8 = {2^3}\)
Suy ra \(n = 3\).
Vậy \(n = 3\).
d) \(B\left( x \right) = \left( {{x^2} - x + 1} \right)\left( {2x + 3} \right)\)
\( = 2{x^3} + 3{x^2} - 2{x^2} - 3x + 2x + 3\)
\( = 2{x^3} + {x^2} - x + 3\)
Ta có \(C\left( x \right) = A\left( x \right) - B\left( x \right)\)
\( = 2{x^3} + 3{x^2} - 4x + 3 - \left( {2{x^3} + {x^2} - x + 3} \right)\)
\( = 2{x^3} + 3{x^2} - 4x + 3 - 2{x^3} - {x^2} + x - 3\)
\( = 2{x^2} - 3x\).
Để tìm nghiệm của đa thức \(C\left( x \right)\), ta cho \(C\left( x \right) = 0\)
Do đó \(2{x^2} - 3x = 0\) hay \(x\left( {2x - 3} \right) = 0\)
Suy ra \(x = 0\) hoặc \(x = \frac{3}{2}\).
Vậy nghiệm của đa thức \(C\left( x \right)\) là \(x \in \left\{ {0;\frac{3}{2}} \right\}\).
Lời giải
a) Tập hợp gồm các kết quả có thể xảy ra đối với số xuất hiện trên quả bóng được rút ra là:
\(A = \left\{ {12;13;14;15;16;17} \right\}\).
Do đó, có 6 kết quả có thể xảy ra.
b) Kết quả thuận lợi cho biến cố \(B\) là \(12\). Do đó có 1 kết quả thuận lợi cho biến cố này.
Xác suất của biến cố \(B\) là \(\frac{1}{6}\).
c) Kết quả thuận lợi cho biến cố \(C\) là \(14;17\). Do đó, có 2 kết quả thuận lợi cho biến cố này.
Xác suất của biến cố \(C\) là \(\frac{2}{6} = \frac{1}{3}\).
Lời giải
a)
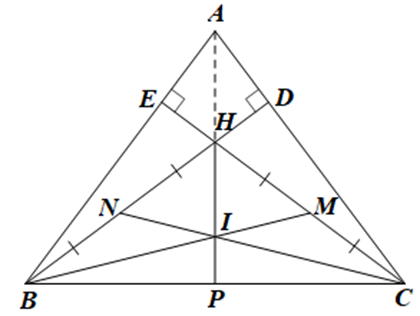
Xét \(\Delta ADB\) và \(\Delta AEC\) có:
\(\widehat {ADB} = \widehat {AEC} = 90^\circ \);
\(AB = AC\) (do \(\Delta ABC\) cân tại \(A\));
\(\widehat {BAC}\) là góc chung.
Do đó \(\Delta ADB = \Delta AEC\) (cạnh huyền – góc nhọn).
Suy ra \(AD = AE\) (hai cạnh tương ứng).
Mà \(AB = AC\) (chứng minh trên)Nên \(AB - AE = AC - AD\) hay \(BE = CD\).
b) Do \(\Delta ADB = \Delta AEC\) (câu a) nên \(\widehat {ABD} = \widehat {ACE}\) (hai góc tương ứng)
Xét \(\Delta BHE\) và \(\Delta CHD\) có:
\(\widehat {BEH} = \widehat {CDH} = 90^\circ \);
\(BE = CD\) (chứng minh câu a);
\(\widehat {EBH} = \widehat {DCH}\)(chứng minh trên).
Do đó \(\Delta BHE = \Delta CHD\) (cạnh góc vuông – góc nhọn kề)
Suy ra \(HB = HC\) (hai cạnh tương ứng)
Tam giác \(HBC\) có \(HB = HC\) nên là tam giác cân tại \(H\).
Xét \(\Delta HDC\) vuông tại \(D\) có \(HC\) là cạnh huyền nên là cạnh có độ dài lớn nhất.
Do đó \(HC > HD\).
Mà \(HB = HC\) (chứng minh trên) nên \(HB > HD.\)
c) Gọi \[P\] là giao điểm của \[HI\] và \[BC\].
\(\Delta HBC\) có hai đường trung tuyến \[BM\] và \[CN\] cắt nhau tại \[I\].
Do đó \[I\] là trọng tâm của \(\Delta HBC\) nên \[HP\] là đường trung tuyến xuất phát từ đỉnh \[H\] của tam giác.
Mà \(\Delta HBC\) cân tại \(H\) nên đường trung tuyến \[HP\] đồng thời là đường cao của tam giác.
Suy ra \(HP \bot BC\) hay \(HI \bot BC\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
\(\Delta ABC\) có \[H\] là giao điểm của hai đường cao \[BD\] và \[CE\] nên \[H\] là trực tâm của \(\Delta ABC\).
Do đó \(AH \bot BC\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra ba điểm \(A,H,I\) cùng nằm trên một đường thẳng vuông góc với \[BC\] tại \(P\).
Hay ba điểm \(A,H,I\) thẳng hàng.
Lời giải
Nhận thấy, số có tổng các chữ số bằng 9 là các số chia hết cho 9.
Do đó, các kết quả thuận lợi cho biến cố này là: \[9;18;27;36;45;54;63;72;81;90\].
Suy ra có 10 kết quả thuận lợi.
Vậy xác suất của biến cố “Số ghi trên vé của Nam là số có tổng các chữ số chia hết cho \[9\]” là: \[\frac{{10}}{{100}} = \frac{1}{{10}}\].