Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 12
24 người thi tuần này 4.6 8.4 K lượt thi 4 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 2
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 3
Bộ 5 đề thi học kì 1 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 1
Bộ 5 đề thi giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
5 câu Trắc nghiệm Tập hợp các số hữu tỉ có đáp án (Nhận biết)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
a) Dấu hiệu ở đây là: "Thời gian làm xong bài tập Toán (tính bằng phút) của học sinh lớp 7B". (0,5 điểm)
Mốt của dấu hiệu là: M0 = 8 (0,5 điểm)
b) Trung bình cộng của dấu hiệu là:
= = 8,4
Lời giải
a) Thu gọn và sắp xếp các đa thức theo lũy thừa giảm dần của biến:
P(x) = 2x4 + 9x2 – 3x + 7 – x – 4x2 – 2x4
P(x) = (2x4 – 2x4) + (9x2 – 4x2) + (–3x – x) + 7
P(x) = 5x2 – 4x + 7 (0,5 điểm)
Q(x) = – 5x3 – 3x – 3 + 7x – x2 – 2
Q(x) = – 5x3 – x2 + (–3x + 7x) + (–3 – 2)
Q(x) = – 5x3 – x 2 + 4x – 5 (0,5 điểm)
Bậc của đa thức P(x) là 2, bậc của đa thức Q(x) là 3 (0,5 điểm)
b) Ta có:
+) P(x) = 5x2 – 4x + 7
Thay vào đa thức P(x) ta được:
=
c,
|
+ |
Q(x) = – 5x3 – x 2 + 4x – 5 |
|
P(x) = 5x2 – 4x + 7 |
Q(x) + P(x) = – 5x3 + 4x2 + 2 (0,25 điểm)
|
– |
Q(x) = – 5x3 – x 2 + 4x – 5 |
|
P(x) = 5x2 – 4x + 7 |
Ta có: Q(x) + P(x) + 5x2 – 2 = 0
(–5x3 + 4x2 + 2) + 5x2 – 2 = 0
–5x3 + 9x2 = 0
x2(–5x + 9) = 0
Vậy x = 0 hoặc x = .
Lời giải
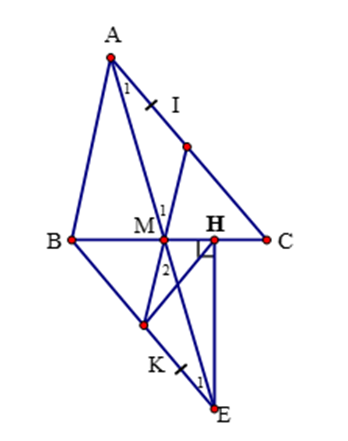
a) Xét tam giác AMC và tam giác EMB có:
MA = ME (GT)
(Hai góc đối đỉnh)
MC = MB (M là trung điểm của BC)
Do đó: tam giác AMC = tam giác EMB (c – g – c)
=> AC = EB (Hai cạnh tương ứng) (1 điểm)
và (Hai góc tương ứng)
Mà và ở vị trí so le trong nên AC // BEXét AMI và EMK có:
AI = EK (GT)
(CM ở câu a)
MA = ME (GT)
Do đó: AMI = EMK (c – g – c)
=> (hai góc tương ứng)
Ta có: = 1800 (Hai góc kề bù) nên = 1800
Ba điểm I, M, K thẳng hàng.Vì BHE vuông tại H có HK là đường trung tuyến (do K là trung điểm của BE)
Nên HK =
BE = 2HK = 2.5 = 10 cm.
Áp dụng định lý Pytago vào tam giác BHE vuông tại H có:
BE2 = BH2 + HE2
102 = BH2 + 62
=> BH2 = 100 – 36 = 64
=> BH = 8 cmLời giải
Vì n có hai chữ số nên 10 n 99 20 2n 198 21 2n + 1 199.
Vì 2n + 1 là số chính phương mà 21 2n + 1 199 nên 2n + 1 {25; 36; 49; 64; 81; 100; 121; 144; 169; 196}.
Vì 2n + 1 lẻ nên 2n + 1 {25; 49; 81; 121; 169} n {12; 24; 40; 60; 84} (1)
Vì 3n + 1 cũng là một số chính phương nên từ (1) n = 40.