10 Bài tập Chứng minh đoạn thẳng bằng nhau, góc bằng nhau, tính độ dài đoạn thẳng, số đo góc (có lời giải)
48 người thi tuần này 4.6 561 lượt thi 10 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 2
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 3
Bộ 5 đề thi học kì 1 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 1
Bộ 5 đề thi giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 4
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
A. 4,5 cm;
B. 3 cm;
C. 6 cm;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: C
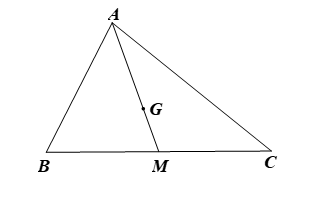
Vì G là trọng tâm ΔABC và AM là đường trung tuyến nên (cm).
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A
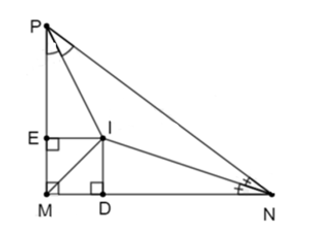
Xét tam giác MNP có các tia phân giác góc N và góc P cắt nhau tại I nên I là giao điểm của ba đường phân giác trong ΔMNP.
Khi đó IE = ID = 5 cm (tính chất ba đường phân giác của tam giác).
Câu 3
A. IN = IM;
B. IE = IB;
C. AI = BI;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: D
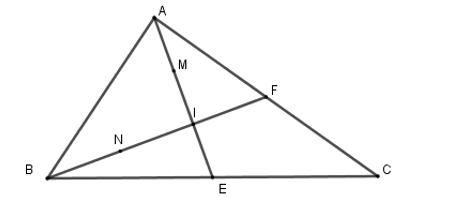
Suy ra nên .
Lại có N là trung điểm của IB suy ra .
Vậy IN = IF.
Câu 4
A. 120°;
B. 60°;
C. 30°;
Lời giải

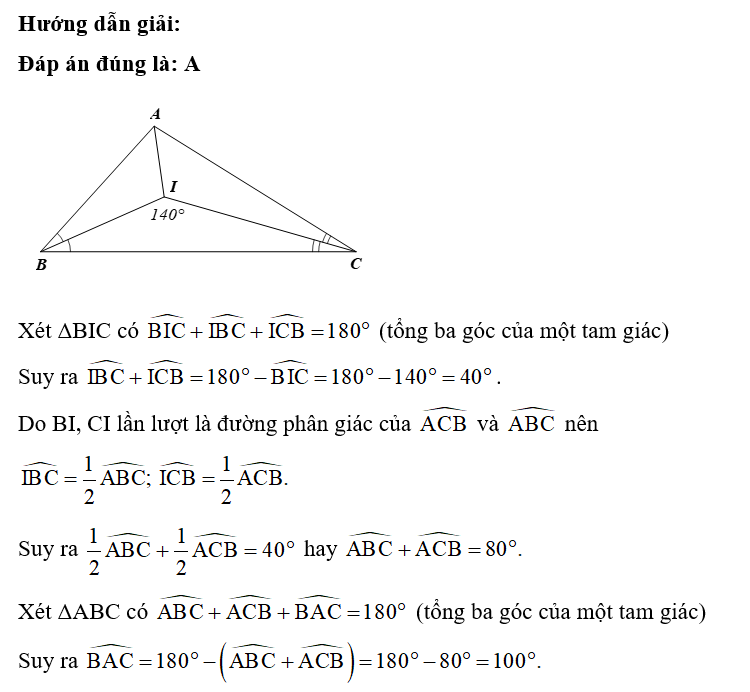
Câu 5
A. 100°;
B. 60°;
C. 30°;
Lời giải
Câu 6
A. 5 cm;
B. 7 cm;
C. 6 cm;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. MN = BM + CN;
B. MN > BM + CN;
C. MN < BM + CN;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. 120°;
B. 60°;
C. 30°;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.