15 câu Trắc nghiệm Toán 7 Cánh diều Bài 2: Tia phân giác của một góc có đáp án
53 người thi tuần này 4.6 2 K lượt thi 15 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 2
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 3
Bộ 5 đề thi học kì 1 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 1
Bộ 5 đề thi giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 4
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
A. Tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau;
B. Tia nằm phía ngoài góc và tạo với hai cạnh của góc đó hai góc bằng nhau;
C. Tia nằm trong góc và tạo với hai cạnh của góc đó hai góc không bằng nhau;
D. Tia nằm phía ngoài góc và tạo với hai cạnh của góc đó hai góc không bằng nhau.
Lời giải
Đáp án đúng là: A
Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
Câu 2
A. Nếu tia Ot là tia phân giác của \[\widehat {xOy}\] thì tia Ot nằm giữa hai tia Ox, Oy;
B. Nếu tia Ot là tia phân giác của \[\widehat {xOy}\] thì \[\widehat {xOt} = \widehat {yOt} = \frac{{\widehat {xOy}}}{2}\];
C. Nếu \[\widehat {xOt} = \widehat {yOt}\] thì tia Ot là tia phân giác của \[\widehat {xOy}\];
D. Nếu \[\widehat {xOt} = \widehat {yOt}\] và tia Ot nằm giữa hai tia Ox, Oy thì tia Ot là tia phân giác của \[\widehat {xOy}\].
Lời giải
Đáp án đúng là: C
Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
Phương án C sai vì chỉ nói đến hai góc bằng nhau mà không có nói đến Ot nằm trong góc.
Lời giải
Đáp án đúng là: B
Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
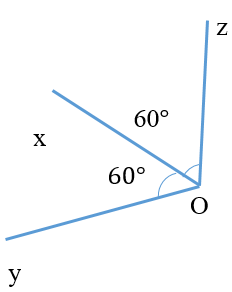
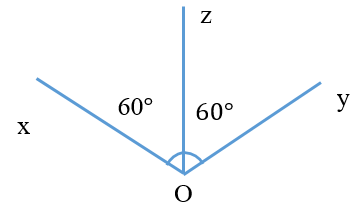
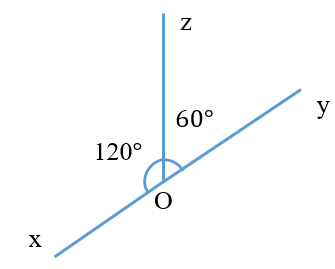
Phương án A, C và D có tia Oz nằm trong góc nhưng không tạo với hai cạnh của góc đó hai góc bằng nhau nên tia Oz trong hình A, C và D không phải tia phân giác.
Chỉ có đáp án B là tia Oz nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau nên suy ra chọn phương án B.
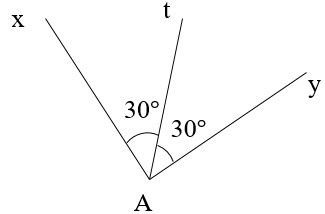
Câu 4
A. 30°;
B. 60°;
C. 120°;
D. 140°.
Lời giải
Đáp án đúng là: B
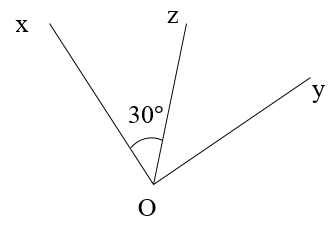
Ta có: \[\widehat {xOz} = \widehat {zOy} = 30^\circ \] (vì Oz là tia phân giác góc xOy)
\[ \Rightarrow \widehat {xOy} = \widehat {xOz} + \widehat {zOy} = 30^\circ + 30^\circ = 60^\circ \]
Vậy \[\widehat {xOy} = 60^\circ \].
Câu 5
A. Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau;
B. Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc không bằng nhau;
C. Tia phân giác của một góc là tia nằm ngoài góc và tạo với hai cạnh của góc đó hai góc bằng nhau;
D. Tia phân giác của một góc là tia nằm ngoài góc và tạo với hai cạnh của góc đó hai góc không bằng nhau.
Lời giải
Đáp án đúng là: A
Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
Câu 6
A. góc vuông;
B. góc nhọn;
C. góc tù;
D. góc bẹt.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 120°;
B. 80°;
C. 60°;
D. 150°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. Oz là tia phân giác của góc xOy;
B. Oz là tia nằm phía trong của góc xOy;
C. Oz là tia nằm phía ngoài của góc xOy;
D. Oz là tia nằm giữa hai cạnh Ox và Oy.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. ;
B. ;
C. ; ;
D. .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. đường đi qua góc đó;
B. trục đối xứng của góc đó;
C. đường nằm trong góc đó;
D. trục cố định của góc đó.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. 60°;
B. 120°;
C. 42°;
D. 30°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. 65°;
B. 40°;
C. 55°;
D. 110°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. 44°;
B. 40°;
C. 60°;
D. 64°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
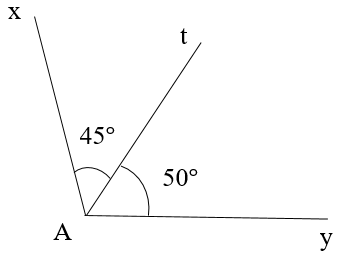
Câu 15
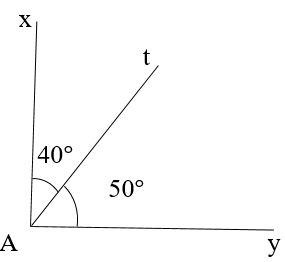
A. \[\widehat {xAt} = \widehat {yAt}\];
B. \[\widehat {xAt} + \widehat {yAt} = 180^\circ \];
C. \[\widehat {xAt} - \widehat {yAt} = 180^\circ \];
D. \[\widehat {xAt} \ne \widehat {yAt}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
 .
.
 ;
; ;
; ;
; .
.