Đề thi cuối học kỳ 2 Toán 6 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 7
20 người thi tuần này 4.6 1.6 K lượt thi 7 câu hỏi 45 phút
🔥 Đề thi HOT:
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
13 Bài tập Một số bài toán thực tế về hình vuông, hình chữ nhật (có lời giải)
21 câu Trắc nghệm Toán 6 Bài 12: Phép chia phân số có đáp án
23 câu Trắc nghệm Toán 6 Bài 13: Hỗn số, số thập phân, phần trăm có đáp án
31 câu Trắc nghiệm Toán 6 Bài tập ôn tập chương 3: Phép chia phân số có đáp án
25 câu Trắc nghiệm Toán 6 Bài 5: Cộng hai số nguyên khác dấu có đáp án
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
a) \(\frac{2}{3} - \left( {\frac{{ - 5}}{7} + \frac{2}{3}} \right)\)\( = \frac{2}{3} + \frac{5}{7} - \frac{2}{3}\)
\( = \left( {\frac{2}{3} - \frac{2}{3}} \right) + \frac{5}{7}\)\( = 0 + \frac{5}{7}\)\( = \frac{5}{7}.\)
b) \[60,7 + 25,5--38,7\]
\[ = \left( {60,7--38,7} \right) + 25,5\]
\[ = 22 + 25,5\]
\( = 47,5.\)
c) \[19\frac{5}{8}:\frac{7}{{12}} - 15\frac{1}{4}:\frac{7}{{12}}\]
\[ = \frac{{157}}{8} \cdot \frac{{12}}{7} - \frac{{61}}{4} \cdot \frac{{12}}{7}\]
\[ = \left( {\frac{{157}}{8} - \frac{{61}}{4}} \right) \cdot \frac{{12}}{7}\]
\[ = \frac{{35}}{8} \cdot \frac{{12}}{7} = \frac{{15}}{2}.\]
d) \(1,9 + \left( {2,51 - 2,13 \cdot 4} \right) - \left( {96 \cdot 2,13 - 99 \cdot 2,51} \right)\)
\( = 1,9 + 2,51 - 2,13 \cdot 4 - 96 \cdot 2,13 + 99 \cdot 2,51\)
\( = \left( {2,51 + 99 \cdot 2,51} \right) - \left( {2,13 \cdot 4 + 96 \cdot 2,13} \right) + 1,9\)
\( = 2,51 \cdot \left( {1 + 99} \right) - 2,13 \cdot \left( {4 + 96} \right) + 1,9\)
\( = 2,51 \cdot 100 - 2,13 \cdot 100 + 1,9\)
\( = 251 - 213 + 1,9\)
\( = 38 + 1,9\)
\( = 39,9.\)
Lời giải
a) \(x - \frac{5}{6} = \frac{{ - 7}}{6}\)
\(x = \frac{{ - 7}}{6} + \frac{5}{6}\)
\(x = \frac{{ - 2}}{6}\)
\(x = \frac{{ - 1}}{3}.\)
Vậy \(x = \frac{{ - 1}}{3}.\)b) \[x + 1,05 = 0,2 - 4,25\]
\[x + 1,05 = - 4,05\]
\[x = - 4,05 - 1,05\]
\[x = - 5,1\].
Vậy \[x = - 5,1.\]c) \[\frac{{x - 1}}{2} = \frac{8}{{x - 1}}\]
\[{\left( {x - 1} \right)^2} = 16\]
\[{\left( {x - 1} \right)^2} = {4^2} = {\left( { - 4} \right)^2}\]Trường hợp 1:
\[x - 1 = 4\]
\[x = 4 + 1\]
\[x = 5\]
Trường hợp 2:
\[x - 1 = - 4\]
\[x = - 4 + 1\]
\[x = - 3\]Lời giải
Chiều rộng của khu vườn là: \(4,5:15\% = 30{\rm{\;(m)}}{\rm{.}}\)
Diện tích của khu vườn là: \(50 \cdot 30 = 1500{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích đào ao là: \(360:\frac{6}{7} = 420{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích trồng rau là: \(65\% \cdot \left( {1500 - 420} \right) = 702{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích trồng hoa là: \(1500 - 420 - 702 = 378{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Lời giải
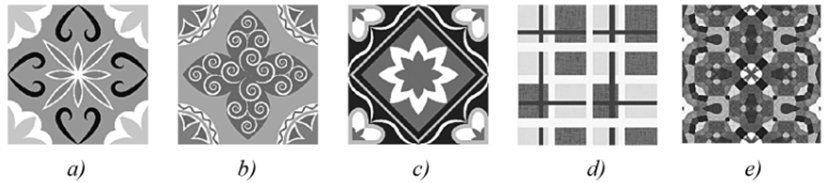
a) Họa tiết của viên gạch hình b) và d) không có tâm đối xứng.
Họa tiết của viên gạch hình a), c), e) vừa có tâm đối xứng, vừa có trục đối xứng.
Vậy có 3 hình thỏa mãn yêu cầu đề bài.
b) Các chữ cái là hình vừa có trục đối xứng, vừa có tâm đối xứng là H, O, I.
Nhóm chữ cái đã cho liên hệ tên một thành phố ở Việt Nam là: HÀ NỘI, hoặc cũng có thể là địa điểm du lịch HỘI AN.
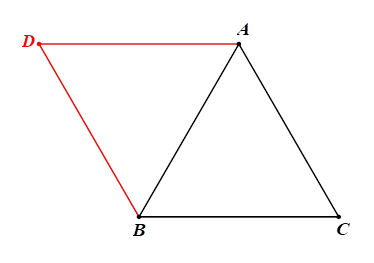
c) Hình đối xứng với tam giác đều \(ABC\) qua trục đối xứng là cạnh \(AB\) được vẽ như sau:
Câu 5
1) Điểm \(A\) nằm trên tia \(Ox\) sao cho \(OA = 4{\rm{\;cm}}.\) Trên tia đối của tia \(Ox\) lấy điểm \(B\) và \(M\) sao cho \(OB = 8{\rm{\;cm}}\) và \(OM = OA.\)
a) Điểm \(O\) có phải là trung điểm của đoạn thẳng \(AM\) không? Tại sao?
b) Tính độ dài đoạn thẳng \(BM\) và \(AB.\)
c) Gọi \(C\) là trung điểm của đoạn thẳng \(AB.\) Chứng minh \(C\) là trung điểm của đoạn thẳng \(OM.\)
2) Ta có thể xem kim phút và kim giờ của đồng hồ là hai tia chung gốc (gốc trùng với trục quay của hai kim). Tại mỗi thời điểm hai kim tạo thành một góc.
a) Biết rằng khi kim giờ và kim phút thay nhau chỉ số 12 và số 6 thì tạo thành một góc có số đo là \(180^\circ .\) Vậy khi hai kim lần lượt chỉ hai số cạnh nhau thì tạo thành một góc có số đo là bao nhiêu độ?
b) Góc tạo bởi kim phút và kim giờ lúc 2 giờ 30 phút có số đo là bao nhiêu độ?
1) Điểm \(A\) nằm trên tia \(Ox\) sao cho \(OA = 4{\rm{\;cm}}.\) Trên tia đối của tia \(Ox\) lấy điểm \(B\) và \(M\) sao cho \(OB = 8{\rm{\;cm}}\) và \(OM = OA.\)
a) Điểm \(O\) có phải là trung điểm của đoạn thẳng \(AM\) không? Tại sao?
b) Tính độ dài đoạn thẳng \(BM\) và \(AB.\)
c) Gọi \(C\) là trung điểm của đoạn thẳng \(AB.\) Chứng minh \(C\) là trung điểm của đoạn thẳng \(OM.\)
2) Ta có thể xem kim phút và kim giờ của đồng hồ là hai tia chung gốc (gốc trùng với trục quay của hai kim). Tại mỗi thời điểm hai kim tạo thành một góc.
a) Biết rằng khi kim giờ và kim phút thay nhau chỉ số 12 và số 6 thì tạo thành một góc có số đo là \(180^\circ .\) Vậy khi hai kim lần lượt chỉ hai số cạnh nhau thì tạo thành một góc có số đo là bao nhiêu độ?
b) Góc tạo bởi kim phút và kim giờ lúc 2 giờ 30 phút có số đo là bao nhiêu độ?
Lời giải
1)

a) Vì điểm \(A\) thuộc tia \[Ox\] và tia \(M\) thuộc tia đối của tia \(Ox\) nên điểm \(O\) nằm giữa hai điểm \(A,\,\,M.\)
Lại có \(OA = OM\) nên điểm \(O\) là trung điểm của đoạn thẳng \(AM.\)
b) ⦁ Ta có \(OM = OA = 4{\rm{\;cm}}\) và \(OB = 8{\rm{\;cm}}\) nên \(OM < OB\)
Mà hai điểm \(B\) và \(M\) nằm trên tia đối của tia \(Ox\) nên điểm \(M\) nằm giữa hai điểm \(O\) và \(B\)
Do đó \(OB = BM + OM\)
Suy ra \(BM = OB - OM = 8 - 4 = 4{\rm{\;(cm)}}{\rm{.}}\)
⦁ Vì điểm \(A\) thuộc tia \[Ox\] và tia \(B\) thuộc tia đối của tia \(Ox\) nên điểm \(O\) nằm giữa hai điểm \(A\) và \(B\)
Do đó \(AB = BO + OA = 8 + 4 = 12{\rm{\;(cm)}}{\rm{.}}\)
c) Vì điểm \(C\) là trung điểm của đoạn thẳng \(AB\) nên \(BC = AC = \frac{{AB}}{2} = \frac{{12}}{2} = 6{\rm{\;(cm)}}{\rm{.}}\)
⦁ Vì điểm \(A\) thuộc tia \[Ox\] và tia \(C\) thuộc tia đối của tia \(Ox\) nên điểm \(O\) nằm giữa hai điểm \(A\) và \(C\)
Do đó \(AC = CO + OA\)
Suy ra \(CO = AC - OA = 6 - 4 = 2{\rm{\;(cm)}}{\rm{.}}\)
⦁ Ta có điểm \(M\) nằm giữa \(C\) và \(B\) nên \(BC = BM + CM\)
Suy ra \(CM = BC - BM = 6 - 4 = 2{\rm{\;(cm)}}{\rm{.}}\)
⦁ Vì điểm \(C\) nằm giữa hai điểm \(M,\,\,O\) và \(MC = CO = 2{\rm{\;cm}}\) nên điểm \(C\) là trung điểm của đoạn thẳng \(OM.\)
2) a) Từ số 12 đến số 6 có 6 khoảng, như vậy, cứ hai kim lần lượt chỉ hai số cạnh nhau trên đồng hồ thì có số đo bằng \(\frac{{180^\circ }}{6} = 30^\circ .\)
b) Khi đồng hồ chỉ 2 giờ 30 phút thì kim giờ nằm giữa số 2 và số 3, kim phút chỉ số 6.
Như vậy, góc được tạo thành có số đo bằng \(\frac{1}{2} \cdot 30^\circ + 3 \cdot 30^\circ = 105^\circ \) (từ giữa số 2 và số 3 đến số 3 là nửa khoảng, từ số 3 đến số 6 là 3 khoảng).
Vậy góc tạo bởi kim phút và kim giờ lúc 2 giờ 30 phút có số đo là \(105^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.