Bộ 10 đề thi Giữa kì 2 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 6

Hướng dẫn giải

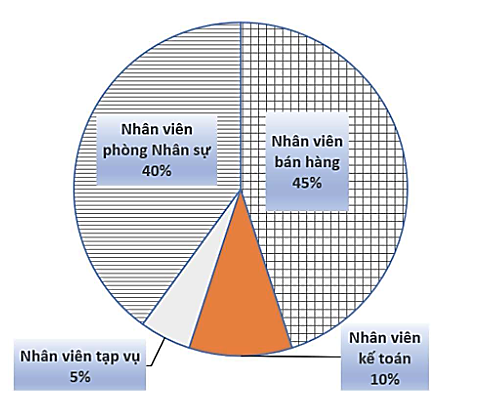
a) Quan sát biểu đồ, ta thấy bộ phận có nhiều nhân viên nhất là bộ phận nhân viên bán hàng (chiếm \(45\% \)).

b) Số nhân viên bộ phận kế toán so với số nhân viên phòng nhân sự là: \(\frac{{10}}{{40}}.100 = 25\% \).

c) Số nhân viên của bộ phận nhân sự là: \(480.40\% = 192\) (nhân viên)

Số nhân viên của bộ phận bán hàng là: \(480.45\% = 214\) (nhân viên)

Số nhân viên của bộ phận tạp vụ là: \(480.5\% = 24\) (nhân viên)

Số nhân viên của bộ phận kế toán là: \(480.10\% = 48\) (nhân viên).

d) Mỗi nhân viên bộ phận kế toán được thưởng số tiền là:

\(10{\rm{ }}800{\rm{ }}000:48 = 225{\rm{ }}000\) (đồng)

Vì mỗi nhân viên được thưởng số tiền như nhau, nên mỗi nhân viên phòng nhân sự cũng được thưởng \({\rm{225 }}000\) đồng.

Do đó, tổng mức thưởng Tết của bộ phận nhân sự là: \(225{\rm{ }}000.192 = 43{\rm{ }}200{\rm{ }}000\) (đồng).

Hướng dẫn giải

a) Các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là: \(A = \left\{ {1;2;3;....;28} \right\}\).

Do đó, có 28 kết quả có thể xảy ra khi rút ngẫu nhiên một thẻ trong hộp.

b) Các kết quả thuận lợi cho biến cố \(X\): “Số xuất hiện trên thẻ được rút ra là số chia hết cho \(5\)” là:

\(X = \left\{ {5;10;15;20;25} \right\}\). Do đó, có 5 kết quả thuận lợi cho biến cố này.

c) Xác suất của biến cố \(X\): “Số xuất hiện trên thẻ được rút ra là số chia hết cho \(5\)” là: \(\frac{5}{{28}}\).

d) Kết quả thuận lợi: “Số xuất hiện trên thẻ được rút ra là số có hai chữ số và khi chia cho 2 và 5 đều dư 1” là: \(\left\{ {1;11;21} \right\}\). Do đó, có 3 kết quả thuận lợi cho biến cố trên.

Vậy xác suất của biến cố đó là: \(\frac{3}{{28}}.\)

Hướng dẫn giải

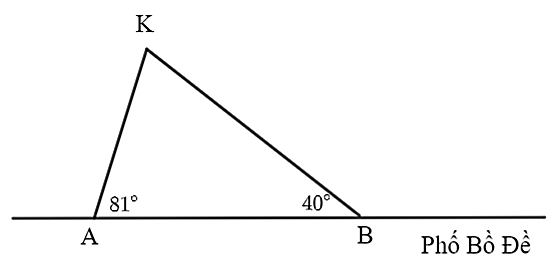
Từ hình vẽ minh họa, xét \(\Delta ABK\), ta có:

\(\widehat A > \widehat B{\rm{ }}\left( {81^\circ > 40^\circ } \right)\), do đó \(KB > KA\) (tính chất của góc và cạnh đối diện trong tam giác).

Vì vậy bạn Cường nên xuống xe ở điểm \(A\) rồi đi bộ đến trường để quãng đường ngắn nhất.

Hướng dẫn giải

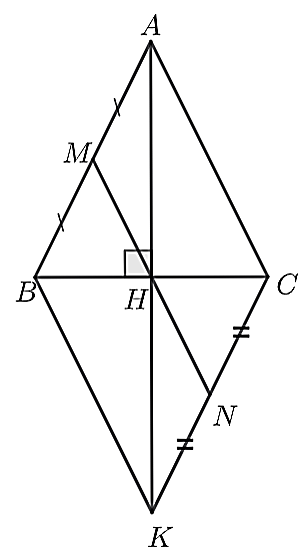
a)

Xét \(\Delta ABH\) và \(\Delta ACH\), có:

\(AB = AC\) (\(\Delta ABC\) cân tại \(A\))

\(AH\): chung (gt)

\(\widehat {AHB} = \widehat {AHC} = 90^\circ \) (gt)

Do đó, \(\Delta ABH = \Delta ACH\) (ch – gn).

b) Xét \(\Delta BHK\) và \(\Delta CHA\), có:

\(BH = HC\) (gt)

\(\widehat {BHK} = \widehat {CHA} = 90^\circ \) (đối đỉnh)

\(HA = HK\) (gt)

Do đó, \(\Delta BHK = \Delta CHA\) (c.g.c)

Suy ra \(\widehat {KBH} = \widehat {HCA}\) (hai góc tương ứng)

Mà hai góc ở vị trí so le trong, suy ra \(AC\parallel BK.\)

c) Xét \(\Delta ABH\) và \(\Delta CHK\), có:

\(HB = HC\) (hai cạnh tương ứng)

\(AH = HK\) (gt)

(đối đỉnh)

Do đó, \(\Delta ABH = \Delta CHK\) (c.g.c)

Suy ra \(\widehat {BAH} = \widehat {HKC}\) (hai góc tương ứng)

Mà hai góc ở vị trí so le trong nên \(AB\parallel KC\).

Lại có \(AB = KC\) (hai cạnh tương ứng).

Mà \(M,N\) là trung điểm của \(AB,CK\). Do đó, \(AM = KN\)

Xét \(\Delta MAH\) và \(\Delta NKH\), có:

\(AM = KN\) (cmt)

\(\widehat {BAH} = \widehat {HKC}\) (cmt)

\(AH = HK\) (gt)

Do đó, \(\Delta MAH = \Delta NKH\) (c.g.c)

Suy ra \(\widehat {MHA} = \widehat {NHK}\) (hai góc tương ứng).

Mà hai góc ở vị trí đối đỉnh, do đó \(M,H,N\) thẳng hàng.

Hướng dẫn giải

Gọi \(n\) (người) là số hành khách nam đã xuống xe \(\left( {n \in {\mathbb{N}^*}} \right)\). Khi đó, trên xe có \(9\) hành khách nữ và \(17 - n\) hành khách nam xuống xe.

Xác suất để chọn được một hành khách nam còn lại trên xe là \(\frac{1}{2}\) nên số hành khách nam còn lại trên xe bằng số hành khách nữ còn lại trên xe.

Do đó, \(17 - n = 9\) hay \(n = 8.\)

Vậy số hành khách nam đã xuống xe là 8 người.