Bộ 10 đề thi Giữa kì 2 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 9
20 người thi tuần này 4.6 3.9 K lượt thi 5 câu hỏi 60 phút
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
Đề kiểm tra học kì 2 Toán 7 có đáp án ( Mới nhất)_ đề số 1
Bài tập chuyên đề Toán 7 Dạng 4: Hai tam giác bằng nhau. Các trường hợp bằng nhau của hai tam giác có đáp án
15 câu Trắc nghiệm Toán 7 Cánh diều Bài 1: Tập hợp Q các số hữu tỉ có đáp án
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
Bài tập: Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác có đáp án
Bài tập: Các góc tạo bởi một đường thẳng cắt hai đường thẳng có đáp án
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
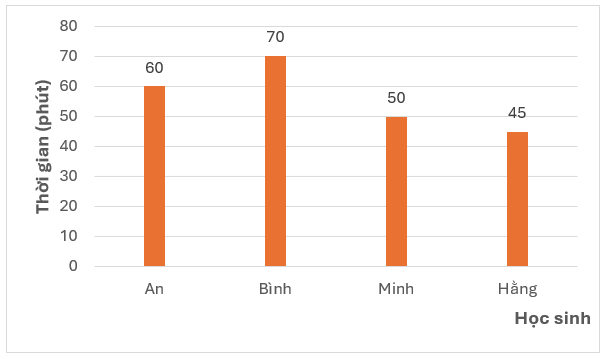
a) Ta có bảng số liệu thống kê thời gian luyện tập của bốn học sinh trên như sau:

b) Từ biểu đồ và bảng thống kê, nhận thấy thời gian bạn Bình tập luyện là nhiều nhất, thời gian bạn Hằng tập luyện là ít nhất.
c) Tổng thời gian bốn bạn luyện tập trong ngày là: \(60 + 70 + 50 + 45 = 225\) (phút)
Thời gian luyện tập trung bình của bốn bạn trong ngày là: \(225:4 \approx 56\) (phút)
d) Thời gian luyện tập của bạn Minh so với thời gian luyện tập của bạn Hằng là: \(\frac{{50}}{{45}}.100 \approx 111,1\% \).
Do đó, thời gian luyện tập của bạn Minh hơn thời gian luyện tập của bạn Hằng số phần trăm là:
\(111,1 - 100 = 11,1\% \)
Lời giải
Hướng dẫn giải
a) Các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là: \(M = \left\{ {1;2;3;4;5;6;7} \right\}\).
Do đó, có 7 kết quả có thể xảy ra khi rút ngẫu nhiên một thẻ trong hộp.
b) Các kết quả thuận lợi cho biến cố: “Rút được thẻ ghi số chẵn” là: \(A = \left\{ {2;4;6} \right\}\).
Do đó, có 3 kết quả thuận lợi cho biến cố trên.
c) Kết quả thuận lợi cho biến cố \(B\): “Rút được thẻ ghi số là số chia cho 5 dư 2” là: \(B = \left\{ {2;7} \right\}\).
Suy ra, xác suất của biến cố \(B\) là: \(\frac{2}{7}.\)
d) Kết quả thuận lợi cho biến cố \(C\): “Rút được thẻ ghi số là hợp số” là: \(C = \left\{ {4;6} \right\}\).
Do đó, xác suất của biến cố này là: \(\frac{2}{7}.\)
Lời giải
Hướng dẫn giải
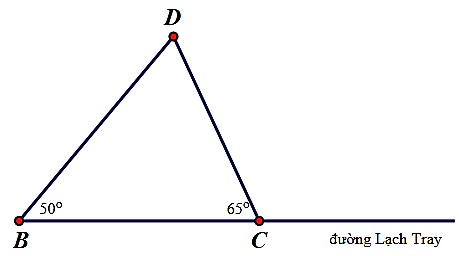
Xét \(\Delta DBC\), có \(\widehat B < \widehat C{\rm{ }}\left( {50^\circ < 65^\circ } \right)\).
Do đó, \(BD > DC\) (quan hệ giữa góc và cạnh trong tam giác)
Vậy bạn Hòa nên xuống đi bộ ở điểm dừng \(B\) để quãng đường đi bộ đến trường là ngắn nhất.
Lời giải
Hướng dẫn giải
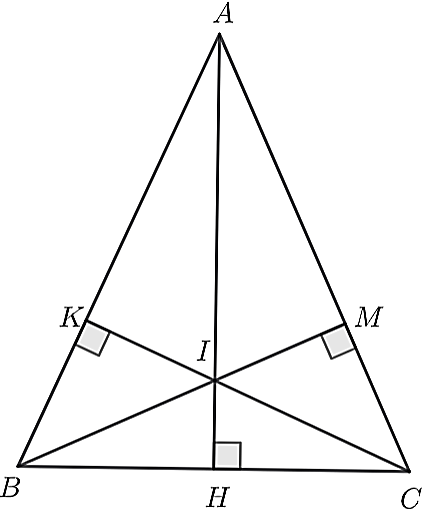
a) Ta có \(\Delta ABC\) cân tại \(A\) và \(AH \bot BC\) tại \(H\) nên \(AH\) vừa là đường cao, vừa là đường trung tuyến của \(\Delta ABC\).
b) Ta có \(BM \bot AC{\rm{ }}\left( {M \in AC} \right)\) nên \(\Delta BMC\) vuông tại \(M\), có \(BC\) là cạnh huyền.
Do đó, \(BM < BC\) (quan hệ giữa các cạnh trong tam giác)
Xét \(\Delta BMA\) vuông tại \(M\) có \(AB\) là cạnh huyền.
Do đó, \(BM < AB\) (1)
Lại có, tam giác \(ABC\) cân tại \(A\) nên \(AB = AC\) (2)
Từ (1) và (2) suy ra \(MB < AC\).
c) Xét \(\Delta KBC\) và \(\Delta MCB\) có:
\(BC\): chung (gt)
\(\widehat {ABC} = \widehat {ACB}\) (tam giác \(ABC\) cân)
\(\widehat {BKC} = \widehat {BMC} = 90^\circ \) (gt)
Suy ra \(\Delta KBC = \Delta MCB\) (ch – gn)
Suy ra \(KB = MC\) (hai cạnh tương ứng).
Lại có: \(\left\{ \begin{array}{l}AB = AK + KB\\AC = AM + MC\end{array} \right.\). Mà \(KB = MC\) (cmt)
Suy ra \(AK = AM\).
Xét \(\Delta KAI\) và \(\Delta MAI\), có:
\(AI\) chung (gt)
\(AK = AM\) (cmt)
\(\widehat {AKI} = \widehat {AMI} = 90^\circ \) (gt)
Suy ra \(\Delta KAI = \Delta MAI\) (ch – cgv)
Suy ra \(KI = MI\) (hai cạnh tương ứng)
Xét \(\Delta KIB\) và \(\Delta MIC\) có:
\(\widehat {IKB} = \widehat {IMC} = 90^\circ \)
\(IK = IM\) (cmt)
\(KB = MC\) (cmt)
Suy ra \(\Delta KIB = \Delta MIC\) (2cgv)
Suy ra \(\widehat {KIB} = \widehat {MIC}\) (hai góc tương ứng)
Mà hai góc ở vị trí đối đỉnh.
Suy ra \(K,I,C\) thẳng hàng.
Lời giải
Hướng dẫn giải
Do mật khẩu nhà bạn Nam là số có ba chữ số và các chữ số này đều là lẻ nên các số đó được tạo thành từ bộ số \(\left\{ {1;3;5;7;9} \right\}\).
Do đó, ta có 5 cách chọn chữ số hàng trăm;
5 cách chọn chữ số hàng chục;
5 cách chọn chữ số hàng đơn vị.
Từ đó, số kết quả có thể xảy ra là: \(5.5.5 = 125\).
Mà Nam chỉ bấm 1 lần nên khả năng xảy ra của mỗi biến cố là như nhau.
Do đó, xác suất để Nam bấm 1 lần mở được cửa là: \(\frac{1}{{125}}.\)