Bộ 10 đề thi Giữa kì 2 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 10

Hướng dẫn giải

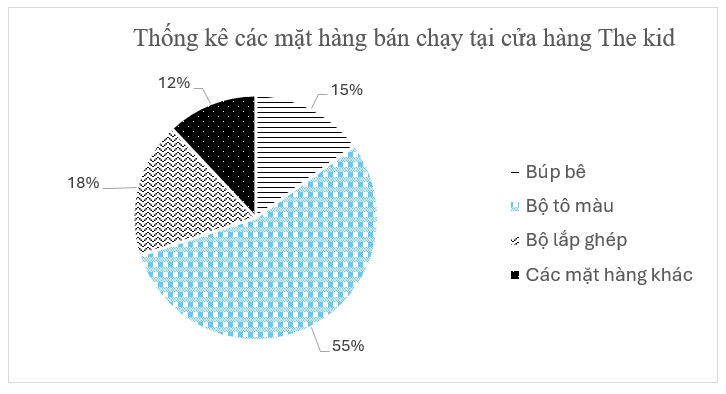
a) Dựa vào biểu đồ, nhận thấy đồ chơi bán chạy nhất trong cửa hàng là bộ tô màu. Đồ chơi ít bán chạy nhất trong cửa hàng là các mặt hàng khác.

b) Bộ tô màu bán được so với số búp bê bán được là: \(\frac{{55}}{{15}}.100 \approx 366,67\% \).

c) Số bộ tô màu bán được là: \(400.55\% = 220\) (sản phẩm)

Số búp bê bán được là: \(400.15\% = 60\) (sản phẩm)

Số bộ lắp ghép bán được là: \(400.18\% = 72\) (sản phẩm)

Số các mặt hàng khác bán được là: \(400.12\% = 48\) (sản phẩm)

d) Số tiền cửa hàng thu về khi bán bộ lắp ghép là: \(72.150{\rm{ }}000 = 10{\rm{ }}800{\rm{ }}000\) (đồng)

Hướng dẫn giải

a) Do danh sách dự thi “Hùng biện Tiếng anh” của lớp 7A có \(10\) bạn học sinh nên có \(10\) kết quả có thể xảy ra.

b) Các kết quả thuận lợi của biến cố “Cô giáo chọn được bạn có số thứ tự không lớn hơn số thứ tự của Hùng” là:

các bạn được đánh số \(\left\{ {1;2;3;4;5;6;7;8} \right\}\). Do đó, có 8 kết quả thuận lợi.

c) Các kết quả thuận lợi của biến cố “Cô giáo chọn được bạn có số thứ tự lớn hơn Hùng” là: \(\left\{ {9;10} \right\}\).

Do đó, xác suất của biến cố trên là: \(\frac{2}{{10}} = \frac{1}{5}\).

d) Xác suất để chọn được bạn Hùng làm đội trưởng là: \(\frac{1}{{10}} = 10\% \).

Do đó, có \(10\% \) để bạn Hùng được làm đội trưởng.

Hướng dẫn giải

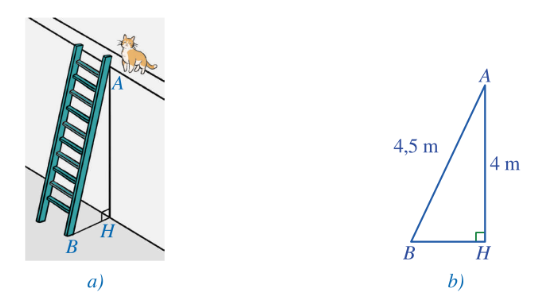
Áp dụng bất đẳng thức về cạnh trong tam giác, ta có:

\(AH + HB > AB\) hay \(HB > AB - AH\) hay \(HB > 4,5 - 4\), suy ra \(HB > 0,5\).

Do đó, khoảng cách từ chân thang đến chân tường lớn hơn \(0,5{\rm{ m}}\).

Do đó, khẳng định của bạn Huệ là sai.

Hướng dẫn giải

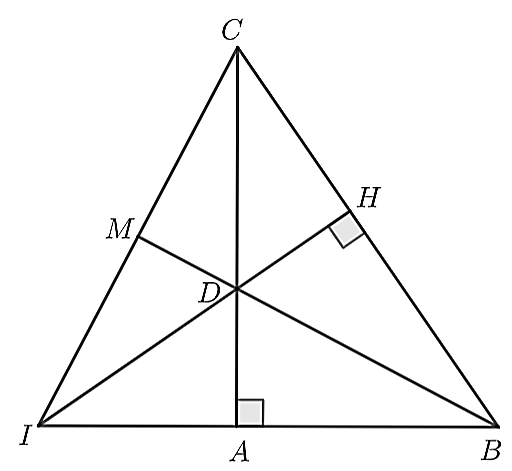
a) Xét

\(\Delta ABD\) và \(\Delta HBD\), có:

\(\widehat {ABD} = \widehat {DBH}\) (\(BD\) là phân giác của \(\widehat B\))

\(BD\) chung (gt)

\(\widehat {DAB} = \widehat {DHB} = 90^\circ \) (gt)

Suy ra \(\Delta ABD = \Delta HBD\) (ch – gn)

Do đó, \(AB = BH\) (hai cạnh tương ứng).

Suy ra \(\Delta ABH\) cân tại \(B\) có \(BD\) là tia phân giác \(\widehat B\).

Suy ra \(BD\) cũng là đường trung trực của \(AH\). Do đó, \(BD \bot AH.\)

b) Do \(\Delta ABD = \Delta HBD\) (cmt) nên \[DA = DH\] (hai cạnh tương ứng)

Xét tam giác \[DAH\] vuông tại \[H\] nên có \[DA\] là cạnh huyền.

Do đó, \[DA > DH\].

Từ đó, suy ra \(DC > AD.\)

c) Chứng minh được \(\Delta ADI = \Delta HDC\) (cgv – gn)

Suy ra \(IA = CH\) (hai cạnh tương ứng)

Mà có \(AB = BH\), suy ra \(AB + AI = BH + HC\) hay \(BI = BC\).

Xét \(\Delta BIM\) và \(\Delta BCM\), có:

\(MI = MC\) (gt)

\(BM\) chung (gt)

\(BI = BC\) (cmt)

Suy ra \(\Delta BIM = \Delta BCM\) (c.c.c)

Do đó, \(\widehat {IBM} = \widehat {CBM}\) (hai góc tương ứng)

Suy ra \(BM\) là phân giác của \(\widehat {ABC}\).

Mà \(BD\) cũng là phân giác của \(\widehat {ABC}\).

Suy ra \(B,D,M\) thẳng hàng.

Hướng dẫn giải

Theo đề, gọi xác suất của biến cố “Lan lấy được quả bóng màu xanh” là \(n\).

Vì biến cố “Lan lấy được quả bóng màu đỏ”, “Lan lấy được quả bóng màu xanh” và “Lan lấy được quả bóng màu vàng” là ba biến cố đồng khả năng.

Do đó, xác suất của ba biến cố này bằng nhau và bằng \(n\).

Từ đó, ta có: \(n + n + n = 1\) hay \(3n = 1\), suy ra \(n = \frac{1}{3}\).

Gọi số quả bóng của màu xanh là \(x,\) ta có: \(\frac{x}{{60}} = \frac{1}{3}\) hay \(x = 20\).

Tương tự ta tính được số quả bóng đỏ và vàng cũng bằng \(20\).

Do đó, số quả bóng màu xanh, đỏ và vàng đều bằng \(20\) quả.