Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 8

Hướng dẫn giải

a) \(\frac{{16}}{x} = \frac{x}{{25}}\) nên \({x^2} = 16.25\) hay \({x^2} = 400\).

Do đó, \({x^2} = {20^2}\) hoặc \({x^2} = {\left( { - 20} \right)^2}\).

Suy ra, \(x = 20\) hoặc \(x = - 20\).

Vậy giá trị cần tìm là \(\left\{ {20; - 20} \right\}\).

b) \(\frac{x}{5} = \frac{y}{7}\) và \(x + y = 36;\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\frac{x}{5} = \frac{y}{7} = \frac{{x + y}}{{5 + 7}} = \frac{{36}}{{12}} = 3\).

Suy ra \(x = 5.3 = 15\) và \(y = 7.3 = 21\).

Vậy \(x = 15\) và \(y = 21\).

c) \(x:y:z = 3:4:5\) và \(x + y - z = 144\)

Ta có \(x:y:z = 3:4:5\) hay \(\frac{x}{3} = \frac{y}{4} = \frac{z}{5}\).

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\frac{x}{3} = \frac{y}{4} = \frac{z}{5} = \frac{{x + y - z}}{{3 + 4 - 5}} = \frac{{144}}{2} = 72\).

Do đó, \(x = 3.72 = 216;{\rm{ }}y = 4.72 = 288;{\rm{ }}z = 5.72 = 360\).

Vậy \(x = 216,y = 288,z = 360.\)

Hướng dẫn giải

2.1. Đổi 30 phút = \(5\) giờ.

Giả sử Lan đi với vận tốc \(10{\rm{ km/h}}\) thì hết \(t\) giờ.

Ta có vận tốc và thời gian Lan đi từ nhà đến trường là hai đại lượng tỉ lệ nghịch nên ta có \(12.0,5 = 10t.\)

Suy ra \(t = \frac{{12.0,5}}{{10}} = 0,6\) giờ.

Ta có \(0,6\) giờ = \(36\) phút.

Vậy nếu Lan đi với vận tốc \(10{\rm{ km/h}}\) thì hết 36 phút.

2.2. Gọi \(x,y,z\) (đồng) theo thứ tự là số tiền điện phải trả của mỗi hộ \(\left( {x,y,z > 0} \right)\).

Theo đề bài, số điện năng tiêu thụ của ba hộ sử dụng tỉ lệ với \(5;7;8\) nên ta có: \(\frac{x}{5} = \frac{y}{7} = \frac{z}{8}\).

Tổng số tiền điện phải trả của ba hộ sử dụng điện trong một tháng là \(820\) nghìn đồng nên \(x + y + z = 820\).

Áp dụng tính chất dãy tỉ số bằng nhau, ta có: \(\frac{x}{5} = \frac{y}{7} = \frac{z}{8} = \frac{{x + y + z}}{{5 + 7 + 8}} = \frac{{820}}{{20}} = 41\).

Suy ra \(x = 5.41 = 205;{\rm{ }}y = 7.41 = 287;{\rm{ }}z = 8.41 = 328\) (thỏa mãn)

Vậy số điện ba hộ phải trả là 205 nghìn đồng, 287 nghìn đồng, 328 nghìn đồng.

Hướng dẫn giải

3.1.

a) Ta có: \(A\left( x \right) = 3{x^2} - 4{x^4} - 5x + 9 + 6{x^4} + 2{x^3} - 5\)

\(A\left( x \right) = \left( { - 4{x^4} + 6{x^4}} \right) + 2{x^3} + 3{x^2} - 5x + 9 - 5\)

\(A\left( x \right) = 2{x^4} + 2{x^3} + 3{x^2} - 5x + 4\).

b) Đa thức \(A\left( x \right)\) có hệ số cao nhất là \(2\), hệ số tự do là \(5\) và bậc là \(4\).

c) Ta có: \(A\left( { - 1} \right) = 2.{\left( { - 1} \right)^4} + 2.{\left( { - 1} \right)^3} + 3.{\left( { - 1} \right)^2} - 5.\left( { - 1} \right) + 4 = 12\).

\(A\left( 0 \right) = {2.0^4} + {2.0^3} + {3.0^2} - 5.0 + 4 = 4\).

\(A\left( 2 \right) = {2.2^4} + {2.2^3} + {3.2^2} - 5.2 + 4 = 54\).

d) Ta có: \(B\left( x \right) - 3{x^2} + 2{x^4} - {x^3} = A\left( x \right)\)

Suy ra \(B\left( x \right) = A\left( x \right) + 3{x^2} - 2{x^4} + {x^3}\) hay \(B\left( x \right) = 2{x^4} + 2{x^3} + 3{x^2} - 5x + 4 + 3{x^2} - 2{x^4} + {x^3}\)

Suy ra \(B\left( x \right) = \left( {2{x^4} - 2{x^4}} \right) + \left( {2{x^3} + {x^3}} \right) + \left( {3{x^2} + 3{x^2}} \right) - 5x + 4\)

\(B\left( x \right) = 3{x^3} + 6{x^2} - 5x + 4\).

3.2. Ta có: \(13 = 12 + 1 = x + 1\).

Do đó, ta có: \(R\left( x \right) = {x^{10}} - \left( {x + 1} \right){x^9} + \left( {x + 1} \right){x^8} - \left( {x + 1} \right){x^7} + ... + \left( {x + 1} \right){x^2} - \left( {x + 1} \right)x + 10\)

Suy ra \(R\left( x \right) = {x^{10}} - {x^{10}} - {x^9} + {x^9} + {x^8} - {x^8} - {x^7} + ... + {x^3} + {x^2} - {x^2} - x + 10\)

\(R\left( x \right) = - x + 10 = - 12 + 10 = - 2\).

Hướng dẫn giải

4.1.

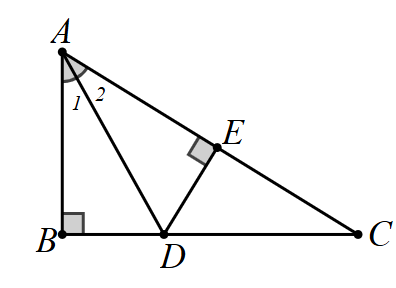
Xét

\(\Delta ABD\) và \(\Delta AED\), có:

\(\widehat B = \widehat E = 90^\circ \)(gt)

\(AD\): chung (gt)

\(\widehat {{A_1}} = \widehat {{A_2}}\) (vì \(AD\) là tia phân giác của \(\widehat {BAC}\))

Do đó, \(\Delta ABD = \Delta AED\) (g.c.g)

Suy ra \(BD = ED\) (hai cạnh tương ứng)

Mà \(BD = 2{\rm{ cm}}\) nên \(ED = 2{\rm{ cm}}{\rm{.}}\)

Vậy khoảng cách từ \(D\) đến đường thẳng \(AC\) là \(2{\rm{ cm}}{\rm{.}}\)

4.2.

Vì tam giác cân nên sẽ có các trường hợp về độ dài ba cạnh như sau.

TH1. \(4{\rm{ cm, 4 cm, 8 cm}}\). Xét thấy \(4{\rm{ cm + 4 cm = 8 cm}}\) nên không thể xảy ra trường hợp này.

TH2. \(4{\rm{ cm, 8 cm, 8 cm}}\). Nhận thấy \(4{\rm{ cm }} + {\rm{ 8 cm}} > {\rm{8 cm}}\) nên thỏa mãn điều kiện về ba cạnh của tam giác.

Do đó, chu vi của tam giác là \(4 + 8 + 8 = 20{\rm{ }}\left( {{\rm{cm}}} \right)\).

Hướng dẫn giải

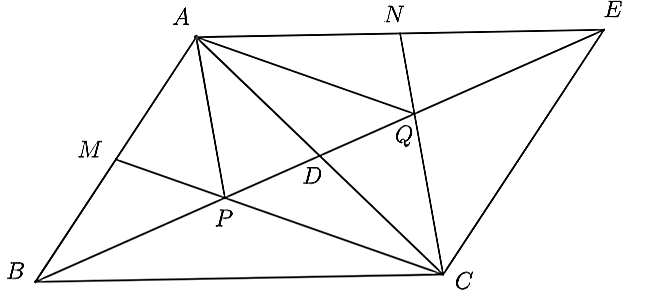
a) Gọi \(M,N\) lần lượt là trung điểm của \(AB,AE\).

Ta có: \(BP = PQ = QE\) và \(BD = DE\).

Mà \(BD = BP + PD;DE = QE + DQ\).

Suy ra \(PD = DQ\).

Hay \(D\) là trung điểm của \(PQ\).

Ta có: \(PD = \frac{1}{2}PQ\) hay \(PD = \frac{1}{2}BP\). Suy ra \(PD = \frac{1}{3}BD\)

Lại có \(BD\) là trung tuyến của \(\Delta ABC\).

Suy ra \(P\)là trọng tâm của \(\Delta ABC\).

Do đó, \(CP\) cắt \(AB\) tại trung điểm \(M.\)

Tương tự ta có: \(QD = \frac{1}{2}PQ = \frac{1}{2}QE\) hay \(QD = \frac{1}{3}ED\).

Do đó, \(Q\) là trọng tâm của tam giác \(AEC\).

Suy ra \(CQ\) cắt \(AE\) tại trung điểm \(N\).

b) Xét \(\Delta ADP\) và \(\Delta CDQ\) có:

\(AD = DC\) (gt)

\(\widehat {ADP} = \widehat {CDQ}\) (đối đỉnh)

\(PD = DQ\) (cmt)

Suy ra \(\Delta ADP = \Delta CDQ\) (c.g.c)

Suy ra \(\widehat {DAP} = \widehat {DCQ}\) (hai góc tương ứng).

Mà hai góc ở vị trí so le trong nên \(CQ\parallel AP.\)

Xét \(\Delta ADQ\) và \(\Delta CDP\) có:

\(AD = DC\) (gt)

\(\widehat {ADQ} = \widehat {CDP}\) (đối đỉnh)

\(PD = DQ\) (cmt)

Suy ra \(\Delta ADQ = \Delta CDP\) (c.g.c)

Suy ra \(\widehat {DAQ} = \widehat {DCP}\) (hai góc tương ứng).

Mà hai góc ở vị trí so le trong nên \(CP\parallel AQ\).