Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 8)

a) Thời gian xúc \[5\,\,000\,\,{{\rm{m}}^{\rm{3}}}\] đầu tiên là: \[\frac{{5\,\,000}}{x}\] (ngày).

a) Phần việc còn lại là: \[11\,\,600 - 5\,\,000 = 6\,\,600{\rm{ }}\left( {{{\rm{m}}^{\rm{3}}}} \right)\].

Năng suất làm việc ở phần việc còn lại: \[x + 25\] \[({{\rm{m}}^{\rm{3}}}\]/ngày)

Thời gian làm nốt phần việc còn lại: \[\frac{{6\,\,600}}{{x + 25}}\] (ngày).

a) Điều kiện xác định của biểu thức \(M\) là \(\left\{ \begin{array}{l}{x^2} - 2x \ne 0\\x \ne 0\end{array} \right.,\) hay \(\left\{ \begin{array}{l}x\left( {x - 2} \right) \ne 0\\x \ne 0\end{array} \right..\)

Khi đó \(\left\{ \begin{array}{l}x \ne 0\\x - 2 \ne 0\end{array} \right.\) nên \(\left\{ \begin{array}{l}x \ne 0\\x \ne 2\end{array} \right..\)

Vậy điều kiện xác định của biểu thức \(M\) là \(x \ne 0\) và \(x \ne 2\).

b) Với \(x \ne 0\) và \(x \ne 2,\) ta có:

\[M = \frac{1}{{{x^2} - 2x}} \cdot \left( {\frac{{{x^2} + 4}}{x} - 4} \right) + 1 = \frac{1}{{x\left( {x - 2} \right)}} \cdot \left( {\frac{{{x^2} + 4}}{x} - \frac{{4x}}{x}} \right) + 1\]

\[ = \frac{1}{{x\left( {x - 2} \right)}} \cdot \frac{{{x^2} + 4 - 4x}}{x} + 1 = \frac{1}{{x\left( {x - 2} \right)}} \cdot \frac{{{{\left( {x - 2} \right)}^2}}}{x} + 1\]

\[ = \frac{{x - 2}}{{{x^2}}} + \frac{{{x^2}}}{{{x^2}}} = \frac{{{x^2} + x - 2}}{{{x^2}}}.\]

Vậy với \(x \ne 0\) và \(x \ne 2,\) thì \(M = \frac{{{x^2} + x - 2}}{{{x^2}}}.\)

Ta có \[\left| {4 - x} \right| = 2\]

Thay \[x = 6\] vào biểu thức \(M = \frac{{{x^2} + x - 2}}{{{x^2}}},\) ta được: \[M = \frac{{{6^2} + 6 - 2}}{{{6^2}}} = \frac{{36 + 6 - 2}}{{36}} = \frac{{10}}{9}.\]

Vậy \(M = \frac{{10}}{9}\) khi \[\left| {4 - x} \right| = 2.\]

c) Với \(x \ne 0\) và \(x \ne 2,\) ta có \[M = \frac{{{x^2} + x - 2}}{{{x^2}}} = 1 + \frac{1}{x} - \frac{2}{{{x^2}}}.\]

Đặt \[\frac{1}{x} = t\,\,\,\left( {t \ne 0;\,\,t \ne \frac{1}{2}} \right),\] khi đó:

\[M = 1 + t - 2{t^2} = - 2\left( {{t^2} - \frac{1}{2}t - \frac{1}{2}} \right) = - 2\left( {{t^2} - 2 \cdot t \cdot \frac{1}{4} + \frac{1}{{16}} - \frac{1}{2} - \frac{1}{{16}}} \right)\]

\[ = - 2\left[ {{{\left( {t - \frac{1}{4}} \right)}^2} - \frac{9}{{16}}} \right] = \frac{9}{8} - 2{\left( {t - \frac{1}{4}} \right)^2}.\]

Vì \[{\left( {t - \frac{1}{4}} \right)^2} \ge 0\] nên \[ - 2{\left( {t - \frac{1}{4}} \right)^2} \le 0,\] do đó \[P \le \frac{9}{8}.\]

Dấu đẳng thức xảy ra khi  tức là \[t = \frac{1}{4}\] (thoả mãn).

Với \(t = \frac{1}{4},\) ta có \[\frac{1}{x} = \frac{1}{4},\] suy ra \[x = 4.\]

Vậy giá trị lớn nhất củ\[t - \frac{1}{4} = 0,\]a \[M\] là \[\frac{9}{8}\] khi \[x = 4.\]

Gọi nồng độ muối trong dung dịch I là \[x\,\,\left( \% \right)\] \(\left( {x > 0} \right).\)

Khi đó khối lượng muối có trong dung dịch I là: \(200 \cdot \frac{x}{{100}} = 2x\) (g).

Do nồng độ muối trong dung dịch I lớn hơn nồng độ muối trong dung dịch II là 20% nên nồng độ muối trong dung dịch II là \(x - 20\,\,\left( \% \right).\)

Khi đó khối lượng muối có trong dung dịch II là: \(300 \cdot \frac{{x - 20}}{{100}} = 3\left( {x - 20} \right)\) (g).

Khối lượng muối trong dung dịch sau khi trộn hai dung dịch là: \(2x + 3\left( {x - 20} \right)\) (g).

Khối lượng dung dịch muối sau khi trộn hai dung dịch là: \(200 + 300 = 500\) (g).

Do sau khi trộn hai dung dịch I và II thì được một dung dịch có nồng độ muối là 33% nên ta có phương trình: \(\frac{{2x + 3\left( {x - 20} \right)}}{{500}} \cdot 100\% = 33\% \)

\(2x + 3x - 60 = 33 \cdot 5\)

\(5x = 225\)

\(x = 45\) (thỏa mãn).

Vậy nồng độ muối của dung dịch I và II lần lượt là \(45\% \) và \(25\% .\)

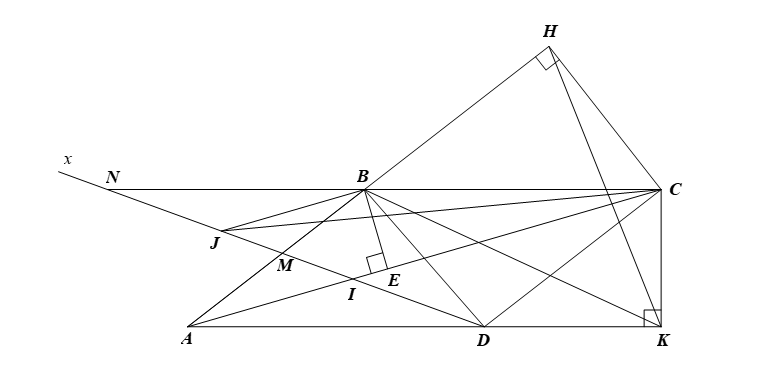
a) Ta có \(ABCD\) là hình bình hành nên \(\widehat {ABC} = \widehat {ADC}\) \(\left( 1 \right)\) (tính chất hình bình hành)

Mà \(\widehat {HBC} = 180^\circ - \widehat {ABC}\) \(\left( 2 \right)\) (hai góc kề bù)

      \(\widehat {KDC} = 180^\circ - \widehat {ADC}\) \(\left( 3 \right)\) (hai góc kề bù)

Từ \(\left( 1 \right)\), \(\left( 2 \right)\), \(\left( 3 \right)\) suy ra \(\widehat {HBC} = \widehat {KDC}.\)

Xét \(\Delta CHB\) và \(\Delta CKD\) có:

\(\widehat {BHC} = \widehat {DKC} = 90^\circ \) và \(\widehat {HBC} = \widehat {KDC}\)

Do đó  (g.g).

Suy ra \(\frac{{CH}}{{CK}} = \frac{{CB}}{{CD}}\) (tỉ số cạnh tương ứng), hay \(\frac{{CH}}{{CB}} = \frac{{CK}}{{CD}}\) (tính chất tỉ lệ thức).

b) Ta có \(\widehat {ABC}\) là góc ngoài của \(\Delta BHC\) nên \(\widehat {ABC} = \widehat {BHC} + \widehat {BCH} = 90^\circ + \widehat {BCH}\)\(\left( 4 \right)\)

Vì \(ABCD\) là hình bình hành nên \(BC\,{\rm{//}}\,AD\) và \(AB = CD\) (tính chất hình bình hành)

Mà \(CK \bot AD\) nên \(CK \bot BC\) nên \(\widehat {BCK} = 90^\circ .\)

Do đó \(\widehat {KCH} = \widehat {BCK} + \widehat {BCH} = 90^\circ + \widehat {BCH}\) \(\left( 5 \right)\)

Từ \(\left( 4 \right)\) và \(\left( 5 \right)\) suy ra \(\widehat {ABC} = \widehat {KCH}.\)

Theo câu a, \(\frac{{CH}}{{CB}} = \frac{{CK}}{{CD}}\) mà \(AB = CD\) nên \(\frac{{CH}}{{CB}} = \frac{{CK}}{{BA}}.\)

Xét \(\Delta CHK\) và \(\Delta BCA\) có: \(\widehat {KCH} = \widehat {ABC}\) và \(\frac{{CH}}{{CB}} = \frac{{CK}}{{BA}}\)

Do đó  (c.g.c).

c) Kẻ \(BE \bot AC\) tại \(E\) \(\left( {E \in AC} \right).\)

Xét \(\Delta AEB\) và \(\Delta AHC\) có: \(\widehat {AEB} = \widehat {AHC} = 90^\circ \) và \(\widehat {HAC}\) là góc chung.

Do đó  (g.g).

Suy ra \(\frac{{AB}}{{AC}} = \frac{{AE}}{{AH}}\) (tỉ số cạnh tương ứng) nên \(AB \cdot AH = AC \cdot AE\)\(\left( 6 \right)\)

Xét \(\Delta BCE\) và \(\Delta CAK\) có:

\(\widehat {BEC} = \widehat {CKA} = 90^\circ \) và \(\widehat {BCE} = \widehat {CAK}\) (hai góc so le trong, \(BC\,{\rm{//}}\,DA)\)

Do đó  (g.g).

Suy ra \(\frac{{BC}}{{CA}} = \frac{{CE}}{{AK}}\) (tỉ số cạnh tương ứng) nên \(BC \cdot AK = AC \cdot CE\)

Mà \(BC = AD\) nên \(AD \cdot AK = AC \cdot CE\) \(\left( 7 \right)\)

Từ \(\left( 6 \right)\) và \(\left( 7 \right)\) suy ra: \(AB \cdot AH + AD \cdot AK = AC \cdot AE + AC \cdot CE\)

Hay \(AB \cdot AH + AD \cdot AK = AC\left( {AE + CE} \right) = A{C^2}.\)

d) Do \(ABCD\) là hình bình hành nên \(AB\,{\rm{//}}\,CD;\;AD\,{\rm{//}}\,BC\) (tính chất hình bình hành)

Hay \(AM\,{\rm{//}}\,CD;\;AD\,{\rm{//}}\,NC.\)

Vì \(AD\,{\rm{//}}\,NC\) nên  do đó \(\frac{{IN}}{{ID}} = \frac{{IC}}{{IA}}\) (tỉ số cạnh tương ứng) \(\left( 8 \right)\)

Vì \(AM\,{\rm{//}}\,DC\) nên  do đó \(\frac{{ID}}{{IM}} = \frac{{IC}}{{IA}}\) (tỉ số cạnh tương ứng) \(\left( 9 \right)\)

Từ \(\left( 8 \right)\) và \(\left( 9 \right)\) suy ra \(\frac{{IN}}{{ID}} = \frac{{ID}}{{IM}},\) nên \(IM \cdot IN = I{D^2}.\)

Gọi \(F\) là giao điểm của \(AB\) và \(ED.\)

Quan sát đường đi của bạn An theo hình vẽ thì đó là tứ giác \(BCDF,\) tứ giác này có \(\widehat {B\,} = \widehat {C\,} = \widehat {D\,} = 90^\circ \) nên là hình chữ nhật.

Mà \(CD = CB = 300\) m nên hình chữ nhật \(BCDF\) là hình vuông.

Do đó \(BC = CD = DF = FB = 300\) (m) và \(\widehat {BFD} = 90^\circ .\)

Ta có \(AF = AB + BF = 900 + 300 = 1\,\,200\) (m); \(EF = FD + DE = 300 + 200 = 500\) (m).

Áp dụng định lí Pythagore cho \(\Delta AEF\) vuông tại \(F\) ta có:

\(A{E^2} = A{F^2} + E{F^2}\)\( = 1\,\,{200^2} + {500^2} = 1{\rm{ }}690{\rm{ }}000.\)

Suy ra \(AE = \sqrt {1{\rm{ }}690{\rm{ }}000} = 1\,\,300\) (m) \( = 1,3\) (km).

Thời gian đi hết quãng đường \(AE\) là: \(\frac{{1,3}}{{13}} = 0,1\) (giờ) \( = 6\) (phút).

Vậy bạn An đi từ nhà đến trường (bằng xe đạp điện) là lúc \(7\) giờ \(6\) phút.