Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 12

1.1.

1.2. Gọi \(x,y\,\,\left( {\rm{g}} \right)\) lần lượt là khối lượng của thanh kim loại thứ nhất và thanh kim loại thứ hai.

Thanh thứ hai nặng hơn thanh thứ nhất \(15,6\,\,{\rm{g}}\) nên \(y - x = 15,6\).

Vì hai thanh kim loại đồng chất nên khối lượng và thể tích của mỗi thanh kim loại là hai đại lượng tỉ lệ thuận. Do đó, ta có \(\frac{x}{5} = \frac{y}{7}\).

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\frac{x}{5} = \frac{y}{7} = \frac{{y - x}}{{7 - 5}} = \frac{{15,6}}{2} = 7,8\).

Suy ra \(x = 7.8.5 = 39\); \(y = 7,8.7 = 54,6\).

Vậy khối lượng của thanh kim loại thứ nhất và thanh kim loại thứ hai lần lượt là \(39\,\,{\rm{g}}\) và \(54,6\,\,{\rm{g}}\).

2.1. Thay \(x = 1,y = 3\) vào biểu thức \(A = \frac{{x + {y^2}}}{5} + xy\), ta được: \(A = \frac{{1 + {3^2}}}{5} + 1.3 = 5\).

Vậy giá trị của biểu thức \(A = 5\) khi \(x = 1,y = 3\).

2.2. a) \(M\left( x \right) = 2{x^4} - 3{x^3} - x + 7{x^3} - 5x + 1\)

               \[ = 2{x^4} + \left( { - 3{x^3} + 7{x^3}} \right) + \left( { - x - 5x} \right) + 1\]

               \[ = 2{x^4} + 4{x^3} - 6x + 1\].

\(N\left( x \right) =  - 2{x^3} + {x^2} + 3{x^4} + 5x - 2{x^4} - 6 + x\)

         \( = \left( {3{x^4} - 2{x^4}} \right) - 2{x^3} + {x^2} + \left( {5x + x} \right) - 6\)

          \( = {x^4} - 2{x^3} + {x^2} + 6x - 6\)

b) Đa thức \(N\left( x \right)\) có bậc là 4, hệ số cao nhất là 1.

c) Ta có \(Q\left( x \right) = M\left( x \right) + N\left( x \right)\)

\(Q\left( x \right) = \left( {2{x^4} + 4{x^3} - 6x + 1} \right) + \left( {{x^4} - 2{x^3} + {x^2} + 6x - 6} \right)\)

         \( = 2{x^4} + 4{x^3} - 6x + 1 + {x^4} - 2{x^3} + {x^2} + 6x - 6\)

         \( = 3{x^4} + 2{x^3} + {x^2} - 5\).

Ta có \(Q\left( x \right) = 3{x^4} + 2{x^3} + 4\)

Suy ra \(3{x^4} + 2{x^3} + {x^2} - 5 = 3{x^4} + 2{x^3} + 4\)

           \({x^2} = 9\)

           \(x = 3\) hoặc \(x =  - 3\).

Vậy \(x \in \left\{ { - 3;3} \right\}\) thì \(Q\left( x \right) = 3{x^4} + 2{x^3} + 4\).

a) Tập hợp gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là:

\(A = \left\{ {1;2;3;4;.....,;27;28} \right\}\).

Vậy có \(28\) phần tử

b) Kết quả thuận lợi của biến cố \(B\) là: \(5;10;15;20;25\).

Do đó, có 5 kết quả thuận lợi cho biến cố này.

Xác suất của biến cố trên là \(\frac{5}{{28}}.\)

c) Kết quả thuận lợi cho biến cố \(C\) là: \(11;21\).

Do đó, có 2 kết quả thuận lợi cho biến cố này.

Xác suất của biến cố \(C\) là \(\frac{2}{{28}} = \frac{1}{{14}}.\)

a) Thể tích nước trong thùng khi đổ \(150\) thùng nước vào bể là: \(150.15 = 2{\rm{ }}250\) (lít)

Đổi \(2{\rm{ }}250{\rm{ }}l = 2{\rm{ }}250{\rm{ d}}{{\rm{m}}^3} = 2,25{\rm{ }}{{\rm{m}}^3}\)

Chiều rộng của bể nước là \(2,25:\left( {2,5.0,5} \right) = 1,8{\rm{ }}\left( {\rm{m}} \right)\).

b) Khi đổ thêm 120 thùng nữa thì đầy bể, tức là khi đổ tất cả \(270\) thùng thì đầy bể.

Do đó, thể tích của bể nước là: \(270.15 = 4{\rm{ }}050\) (lít) = \(4,05{\rm{ }}{{\rm{m}}^3}\).

Chiều cao của bể nước là \(4,05:\left( {2,5.1,8} \right) = 0,9{\rm{ }}\left( {\rm{m}} \right)\).

Vậy chiều cao của bể nước là \(0,9{\rm{ m}}\).

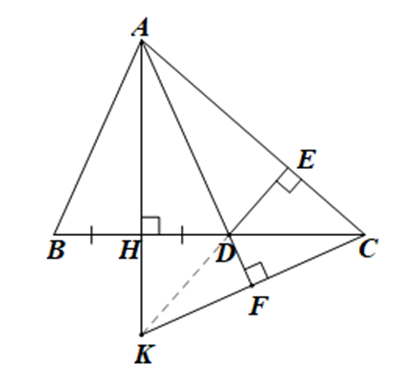
a) Xét \(\Delta ABC\) có \(AB < AC\) nên \(\widehat C < \widehat B\).

Mà \(\widehat C = 90^\circ  - \widehat {HAC}\) và \(\widehat B = 90^\circ  - \widehat {BAH}\).

Do đó \[90^\circ  - \widehat {HAC} < 90^\circ  - \widehat {BAH}\] hay \(\widehat {HAC} > \widehat {BAH}\).

b) Xét \(\Delta ABH\) và \(\Delta ADH\) có:

\(\widehat {AHB} = \widehat {AHD} = 90^\circ \);

\(AH\) là cạnh chung;

\(HB = HD\) (giả thiết).

Do đó \(\Delta ABH = \Delta ADH\) (hai cạnh góc vuông).

Suy ra \(AB = AD\) (hai cạnh tương ứng).

Tam giác \(ABD\) có \(AB = AD\) nên là tam giác cân tại \(A\).

c) Kéo dài \(AH\) và \(CF\) cắt nhau tại \(K\).

Xét  \(\Delta AKC\) có \(CH \bot AK,AF \bot CK\), \(CH\) cắt \[AF\] tại \(D\) nên \(D\) là  trực tâm của \(\Delta AKC\).

Suy ra \(KD \bot AC\)

Mà \(DE \bot AC\) nên ba điểm \(K,D,E\) thẳng hàng.

Vậy ba đường thẳng \(AH,DE,CF\) đồng quy.