7 câu Trắc nghiệm Đường trung trực của một đoạn thẳng có đáp án (Thông hiểu)

Hướng dẫn giải

Đáp án đúng là: B

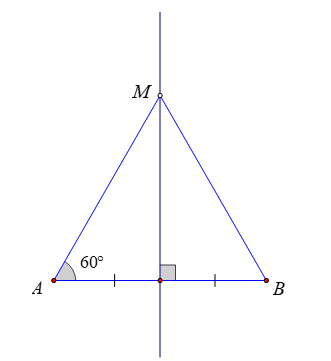
M thuộc đường trung trực của đoạn thẳng AB nên MA = MB (tính chất đường trung trực)

Do đó tam giác MAB cân tại M

Mà $\widehat{MAB}=60°$ nên tam giác MAB đều.

Hướng dẫn giải

Đáp án đúng là: B

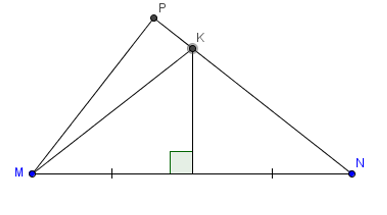
Ta có: K thuộc đường trung trực của MN (giả thiết)

Suy ra KM = KN (tính chất)

Chu vi ∆KMP = MP + PK + KM = MP + PK + KN = MP + PN = 9 + 16 = 25 (cm)

Vậy chu vi ∆KMP là 25 cm.

Hướng dẫn giải

Đáp án đúng là: C

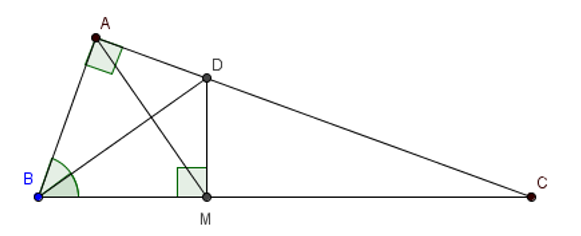
Xét hai tam giác vuông BAD và BMD có:

BD là cạnh chung

$\widehat{ABD}=\widehat{MBD}$ (vì BD là tia phân giác góc ABM)

Suy ra ∆BAD = ∆BMD (cạnh huyền – góc nhọn)

Do đó: BA = BM; AD = MD (2 cạnh tương ứng)

Vì BA = BM nên B thuộc đường trung trực của AM

AD = MD nên D thuộc đường trung trực của AM

Suy ra BD là đường trung trực của AM.

Vậy AB = AM là khẳng định sai.

Hướng dẫn giải

Đáp án đúng là: C

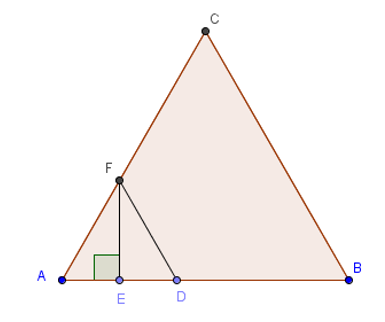
Tam giác ABC đều nên AB = AC = BC = 20 (cm) (tính chất)

AD + DB = AB

Suy ra: 8 + DB = 20

DB = 20 – 8 = 12 (cm)

F thuộc đường trung trực của AD (giả thiết) nên FA = FD (tính chất)

Chu vi tứ giác BCFD = BC + CF + FD + DB

                                 = BC + CF + FA + DB

                                 = BC + CA + DB

                                 = 20 + 20 + 12 = 52 (cm)

Vậy chu vi tứ giác BCFD là 52 cm.

Hướng dẫn giải

Đáp án đúng là: B

Gọi ba điểm phân biệt H, I, K thẳng hàng cùng thuộc đường thẳng p

Ta có: m là đường trung trực của HI (giả thiết) nên m ⊥ HI hay m ⊥ p (1)

n là đường trung trực của IK (giả thiết) nên n ⊥ IK hay n ⊥ p (2)

Từ (1) và (2) suy ra m // n.