Đề thi giữa kì 1 môn Toán lớp 9 Cánh diều có đáp án (Đề 5)
17 người thi tuần này 4.6 1.6 K lượt thi 11 câu hỏi 60 phút
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 1: Đại số)
Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất)- Đề số 1
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
15 câu Trắc nghiệm Toán 9 Chân trời sáng tạo Bài 1. Phương trình quy về phương trình bậc nhất một ẩn có đáp án
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: B
Dễ dàng thấy rằng:
⦁ Giá trị \(x = 0\) không là nghiệm của phương trình \(\left( {x - 1} \right)\left( {x + 1} \right) = 0\).
⦁ Giá trị \(x = 0\) và \(x = - 1\) là nghiệm của phương trình \(x\left( {x + 1} \right) = 0\).
⦁ Giá trị \(x = - 1\) không là nghiệm của phương trình \(x = 0\) và phương trình \(x\left( {x - 1} \right) = 0\)
Vậy ta chọn phương án B.
Lời giải
Đáp án đúng là: B
Từ phương trình \(x - 2y = 0\) ta có \(x = 2y\) và \(y = \frac{x}{2}\).
Như vậy, công thức nghiệm tổng quát của phương trình ta có viết là \(\left( {x;\,\,\frac{x}{2}} \right)\) với \(x \in \mathbb{R}\) hoặc \(\left( {2y;\,\,y} \right)\) với \(y \in \mathbb{R}\).
Vậy ta chọn phương án B.
Lời giải
Đáp án đúng là: C
Sử dụng máy tính cầm tay ta lần lượt bấm các phím
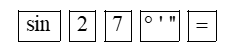
Trên màn hình hiện kết quả \(0,4539904997\), làm tròn kết quả đến chữ số thập phân thứ ba, ta được \(0,454\). Như vậy \(\sin 27^\circ \approx 0,454\).
Lời giải
Đáp án đúng là: B
|
Xét \(\Delta ABC\) vuông tại \(A,\) ta có: ⦁ \[B{C^2} = A{C^2} + A{B^2}\] hay \({a^2} = {b^2} + {c^2}\) (định lí Pythagore); ⦁ \[AC = BC \cdot \sin B = BC \cdot \cos C\] hay \(b = a \cdot \sin B = a \cdot \cos C\); ⦁ \(AB = BC \cdot \sin C = BC \cdot \cos B\) hay \(c = a \cdot \sin C = a \cdot \cos B\); Như vậy các khẳng định A, C, D đều đúng. Ta chọn phương án B. |
|
Lời giải
Hướng dẫn giải
Đáp án: a) Đ;b) S;c) Đ; d) S.
⦁ Do \(a > 1\) nên \(a - 1 > 0\). Do đó ý a) là đúng.
⦁ Do \(a > b\) nên \(a - b > 0\). Do đó ý b) là sai.
⦁ Do \(1 > b\) hay \(b < 1\) nên \(b - 1 < 0\), mà \(a - 1 > 0\) suy ra \(\left( {a - 1} \right)\left( {b - 1} \right) < 0.\) Do đó ý c) là đúng.
⦁ Ta có \(a - 2b = \left( {a - 1} \right) - 2\left( {b - 1} \right) - 1\)
Do \(b - 1 < 0\) nên \( - 2\left( {b - 1} \right) > 0\).</>
Lại có \(a - 1 > 0\) nên \(\left( {a - 1} \right) - 2\left( {b - 1} \right) > 0,\) suy ra \(\left( {a - 1} \right) - 2\left( {b - 1} \right) - 1 > - 1\)
Như vậy \(2a - b > - 1.\) Do đó ý d) là sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.