Bài 12: Dấu hiệu chia hết cho 3, cho 9
119 người thi tuần này 4.6 3.5 K lượt thi 19 câu hỏi
🔥 Đề thi HOT:
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
Dạng 4: Trung điểm của đoạn thẳng có đáp án
Dạng 4: Một số bài tập nâng cao về lũy thừa
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 2)
Đề thi cuối học kỳ 2 Toán 6 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 2
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Ta có: 1 + 8 + 7 = 16 không chia hết cho 3 và 9
1 + 3 + 4 + 7 = 15 chia hết cho 3, không chia hết cho 9
2 + 5 + 1 + 5 = 13 không chia hết cho 3 và 9
6 + 5 + 3 + 4 = 18 chia hết cho 3 và 9.
9 + 3 + 2 + 5 + 8 = 27 chia hết cho 3 và 9.
Theo tính chất chia hết cho 3 và 9 ta có:
– Các số chia hết cho 3 gồm: 1347; 6534; 93258.
– Các số chia hết cho 9 gồm: 6534; 93258.
Câu 2
Cho các số 3564; 4352; 6531; 6570; 1248
Viết tập hơp A các số chia hết cho 3 trong các số trên.
Lời giải
Ta có: 3 + 5 + 6 + 4 = 18 chia hết cho 3 và 9.
4 + 3 + 5 + 2 = 14 không chia hết cho 3 và 9.
6 + 5 + 3 + 1 = 15 chia hết cho 3 nhưng không chia hết cho 9.
6 + 5 + 7 + 0 = 18 chia hết cho 3 và 9.
1 + 2 + 4 + 8 = 15 chia hết cho 3 nhưng không chia hết cho 9.
Do đó:
Tập hợp các số chia hết cho 3 là A = {3564; 6531; 6570; 1248}
Câu 3
Cho các số 3564; 4352; 6531; 6570; 1248
Viết tập hợp B các số chia hết cho 9 trong các số trên.
Lời giải
Ta có: 3 + 5 + 6 + 4 = 18 chia hết cho 3 và 9.
4 + 3 + 5 + 2 = 14 không chia hết cho 3 và 9.
6 + 5 + 3 + 1 = 15 chia hết cho 3 nhưng không chia hết cho 9.
6 + 5 + 7 + 0 = 18 chia hết cho 3 và 9.
1 + 2 + 4 + 8 = 15 chia hết cho 3 nhưng không chia hết cho 9.
Do đó:
Tập hợp các số chia hết cho 9 là B = {3564; 6570}.
Câu 4
Cho các số 3564; 4352; 6531; 6570; 1248
Dùng kí hiệu ⊂ để thể hiện quan hệ giữa hai tập hợp trên
Lời giải
Ta có: 3 + 5 + 6 + 4 = 18 chia hết cho 3 và 9.
4 + 3 + 5 + 2 = 14 không chia hết cho 3 và 9.
6 + 5 + 3 + 1 = 15 chia hết cho 3 nhưng không chia hết cho 9.
6 + 5 + 7 + 0 = 18 chia hết cho 3 và 9.
1 + 2 + 4 + 8 = 15 chia hết cho 3 nhưng không chia hết cho 9.
Do đó:
Vì mỗi phần tử của tập B đều là phần tử của tập A nên B ⊂ A.
Lời giải
1 + 2 + 5 +1 = 9 chia hết cho 3 và 9.
5 + 3 + 1 + 6 = 15 chia hết cho 3 nhưng không chia hết cho 9.
Do đó:
1251 ⋮ 3 và 5316 ⋮ 3 ⇒ 1251 + 5316 ⋮ 3.
1251 ⋮ 9 và 5316 ⋮̸ 9 nên 1251 + 5316 ⋮̸ 9.
Lời giải
5 + 4 + 3 + 6 = 18 chia hết cho 3 và 9.
1 + 3 + 2 + 4 = 10 không chia hết cho cả 3 và 9.
Do đó:
5436 ⋮ 3 và 1324 ⋮̸ 3 nên 5436 – 1324 ⋮̸ 3.
5436 ⋮ 9 và 1324 ⋮̸ 9 nên 5436 – 1324 ⋮̸ 9.
Lời giải
Ta có: 1.2.3.4.5.6 chia hết cho 3.
1.2.3.4.5.6 = 1.2.4.5.(3.6) = 1.2.4.5.18 = 1.2.4.5.2.9 chia hết cho 9.
27 chia hết cho 3 và 9.
Do đó 1.2.3.4.5.6 + 27 chia hết cho 3 và 9.
Lời giải
Ta có: 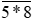
Mà 0 ≤ * ≤ 9 nên * = 2; 5 hoặc 8.
Vậy các số 528; 558; 588 ⋮ 3.
Lời giải
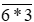
Mà 0 ≤ * ≤ 9 nên * = 0 hoặc 9.
Vậy các số 603; 693 ⋮ 9.
Lời giải
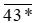
* = 0 thì 4 + 3 + 0 = 7 ⋮̸ 3 nên 430 ⋮̸ 3 (loại).
* = 5 thì 4 + 3 + 5 = 12 ⋮ 3 nên 435 ⋮ 3 (thỏa mãn).
Vậy 435 chia hết cho cả 3 và 5.
Câu 11
Điền chữ số vào dấu * để:
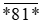
Lời giải
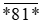
Do đó số cần tìm có dạng
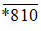
Mà 0 < * < 10 nên * = 9.
Vậy số chia hết cho cả 2, 3, 5, 9 là 9810.
Câu 12
Dùng ba trong bốn chữ số 4, 5, 3, 0 hãy ghép thành các số tự nhiên có ba chữ số sao cho các số đó:
Chia hết cho 9
Lời giải
Bộ ba số có tổng chia hết cho 9 là (4; 5; 0) (4 + 5 + 0 = 9)
Do đó các số được lập từ ba số trên cũng chia hết cho 9 .
Ta lập được các số là 450; 405; 540; 504.
Câu 13
Dùng ba trong bốn chữ số 4, 5, 3, 0 hãy ghép thành các số tự nhiên có ba chữ số sao cho các số đó:
Chia hết cho 3 và không chia hết cho 9
Lời giải
Bộ ba số có tổng chia hết cho 3 nhưng không chia hết cho 9 là (4 ; 5 ; 3)
(4 + 5 + 3 = 12 chia hết cho 3 nhưng không chia hết cho 9).
Do đó các số được lập từ ba số trên cũng chia hết cho 3 nhưng không chia hết cho 9.
Ta lập được các số: 453; 435; 543; 534; 345; 354
Lời giải
Số tự nhiên nhỏ nhất có năm chữ số chia hết cho 3 là 10002
Lời giải
Số tự nhiên nhỏ nhất có năm chữ số chia hết cho 9 là 10008.
Câu 16
Điền dấu "X" vào ô thích hợp trong các câu sau:
| Câu | Đúng | Sai |
| a) Một số chia hết cho 9 thì chia hết cho 3. | ||
| b) Một số chia hết cho 3 thì chia hết cho 9. | ||
| c) Một số chia hết cho 15 thì chia hết cho 3. | ||
| d) Mộtsố chia hết cho 45 thì chia hết cho 9. |
Lời giải
| a) | X | |
| b) | X | |
| c) | X | |
| d) | X |
Giải thích:
a) Đúng vì 9 ⋮ 3 nên số chia hết cho 9 sẽ chia hết cho 3.
b) Sai. Ví dụ: 15 ⋮ 3 nhưng 15 ⋮̸ 9.
c) Đúng vì 15 ⋮ 3 nên số chia hết cho 15 sẽ chia hết cho 3.
d) Đúng vì 45 ⋮ 9 nên số chia hết cho 45 sẽ chia hết cho 9.
Câu 17
Một số có tổng các chữ số chia cho 9 (cho 3) dư m thì số đó chia cho 9 (cho 3) cũng dư m.
Ví dụ: Số 1543 có tổng các chữ số bằng 1 + 5 + 4 + 3 = 13. Số 13 chia 9 dư 4 chia cho 3 dư 1. Do đó số 1543 chia cho 9 dư 4, chia cho 3 dư 1.
Tìm số dư khi chia mỗi số sau cho 9, cho 3: 1546; 1527; 2468; 1011.
Lời giải
+) 1546 có 1 + 5 + 4 + 6 =16. 16 chia 3 dư 1, chia 9 dư 7.
Do đó 1546 chia 3 dư 1, chia 9 dư 7.
+) 1527 có 1 + 5 + 2 + 7 = 15. Ta thấy 15 chia 9 thư 6 và 15 chia 3 dư 0 nên 1527 chia 9 dư 6, chia hết cho 3.
+) 2468 có 2 + 4 + 6 + 8 = 20. 20 chia 9 dư 2, chia 3 dư 2.
Do đó 2468 chia 3, chia 9 đều dư 2.
+) 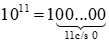
Do đó 1011 chia 3, chia 9 đều dư 1.
Lời giải
16 = 9 + 7 nên 16 chia 9 dư 7.
213 có tổng các chữ số 2 + 1 + 3 = 6 chia 9 dư 6 nên 213 chia 9 dư 6.
827 có tổng các chữ số 8 + 2 + 7 = 17 chia 9 dư 8 nên 827 chia 9 dư 8.
468 có tổng các chữ số 4 + 6 + 8 = 18 ⋮ 9 nên 468 ⋮ 9.
Do đó ta có bảng sau :
| a | 16 | 213 | 827 | 468 |
| m | 7 | 6 | 8 | 0 |
Câu 19
Trong phép nhân a.b = c gọi:
m là số dư cua a khi cho 9, n là số dư của b khi chia cho 9,
r là số dư của tích m.n khi chia cho 9, d là số dư của c khi chia cho 9.
Điền vào ô trống rồi so sánh r và d trong mỗi trường hợp sau:
| a | 78 | 64 | 72 |
| b | 47 | 59 | 21 |
| c | 3666 | 3776 | 1512 |
| m | 6 | ||
| n | 2 | ||
| r | 3 | ||
| d | 3 |
Lời giải
– Ở cột thứ hai : a = 64 ; b = 59 ; c = 3776.
Ta có : 64 = 7.9 + 1 nên 64 chia 9 dư 1 hay m = 1.
59 = 6.9 + 5 nên 59 chia 9 dư 5 hay n = 5.
Tích m.n = 5 chia 9 dư 5 nên r = 5.
c = 3776 có 3 + 7 + 7 + 6 = 23 chia 9 dư 5 nên c chia 9 dư 5 hay d = 5.
– Ở cột thứ ba: a = 72; b = 21; c = 1512.
Ta có : 72 = 8.9 chia hết cho 9 nên m = 0.
21 = 9.2 + 3 nên 21 chia 9 dư 3 hay n = 3.
Tích m.n = 0 ⋮ 9 nên r = 0.
c = 1512 có 1 + 5 + 1 + 2 = 9 ⋮ nên 1512 ⋮ 9 hay d = 0.
Do đó ta có bảng:
| a | 78 | 64 | 72 |
| b | 47 | 59 | 21 |
| c | 3666 | 3776 | 1512 |
| m | 6 | 1 | 0 |
| n | 2 | 5 | 3 |
| r | 3 | 5 | 0 |
| d | 3 | 5 | 0 |
694 Đánh giá
50%
40%
0%
0%
0%