10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải
40 người thi tuần này 4.6 170 lượt thi 10 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: D
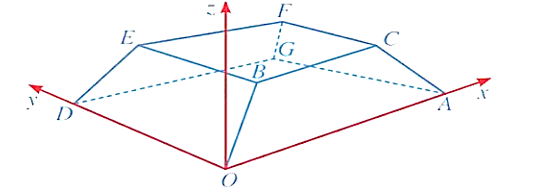
Vì B(3k; 2k; k) (CBEF): z = 3 nên k = 3.
Suy ra B(9; 6; 3). Khi đó a + b + c = 18.
Lời giải
Đáp án đúng là: D
Do mặt dưới của mái nhà thuộc mặt phẳng vuông góc với trục Oz và đi qua A(3; 4; 33) nên phương trình mặt phẳng chứa mặt dưới của mái nhà là: z – 33 = 0.
Khoảng cách từ điểm D đến mặt phẳng chứa mặt dưới của mái nhà bằng:
\(\frac{{\left| {35 - 33} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} }} = 2\).
Lời giải
Đáp án đúng là: B
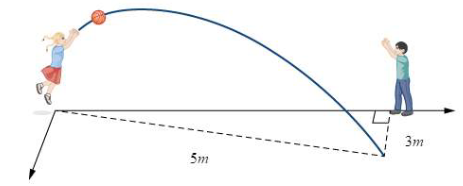
Chọn hệ trục tọa độ như hình vẽ
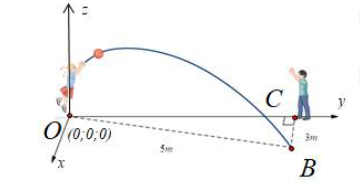
Ta có \(OC = \sqrt {O{B^2} - B{C^2}} = 4\). Suy ra B(3; 4; 0).
Mặt phẳng chứa quỹ đạo đi qua O(0; 0; 0) và nhận \(\overrightarrow k \left( {0;0;1} \right),\overrightarrow {OB} \left( {3;4;0} \right)\) làm vectơ chỉ phương.
Suy ra vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow k ,\overrightarrow {OB} } \right] = \left( { - 4;3;0} \right)\).
Vậy phương trình mặt phẳng chứa quỹ đạo của quả bóng là
−4(x – 0) + 3(y – 0) + 0(z – 0) = 0 4x – 3y = 0.
Do đó a + c = 4.
Câu 4
A. 2,58;
B. 2,85;
C. 3,85;
D. 3,58.
Lời giải
Đáp án đúng là: B
Ta có \(\overrightarrow {AB} = \left( {3;1;0} \right),\overrightarrow {AC} = \left( {6;2; - 1} \right)\).
Mặt phẳng (ABC) có vectơ pháp tuyến là \(\overrightarrow n = \left( { - 1;3;0} \right)\) nên phương trình (ABC):
x – 3y + 3 = 0.
Vậy khoảng cách \(d\left( {D,\left( {ABC} \right)} \right) = \frac{{\left| {1.6 + 3} \right|}}{{\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }} = \frac{{9\sqrt {10} }}{{10}} \approx 2,85\).
Lời giải
Đáp án đúng là: A
Vì (Q) // (P) nên (Q) có một vectơ pháp tuyến là \(\overrightarrow n = \left( {6;5;1} \right)\).
Nên phương trình mặt phẳng (Q): 6x + 5y + z – 12 = 0.
Do đó A + B + C + D = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.