10 bài tập Xác định vectơ, chỉ ra các yếu tố của vectơ có lời giải
97 người thi tuần này 4.6 539 lượt thi 10 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Câu 1
A. \(\overrightarrow {AA} \);
B. \(\overrightarrow {BA} \);
C. \(\overrightarrow {AB} \);
D. \(\overrightarrow {BB} \).
Lời giải
Đáp án đúng là: C
Vectơ có điểm đầu là A, điểm cuối là B là \(\overrightarrow {AB} \).
Câu 2
A. \(\overrightarrow {BB} \);
B. \(\overrightarrow {BA} \);
C. \(\overrightarrow {BC} \);
D. \(\overrightarrow {CA} \).
Lời giải
Đáp án đúng là: A
Vì vectơ – không là vectơ có điểm đầu điểm cuối trùng nhau nên \(\overrightarrow {BB} = \overrightarrow 0 \).
Câu 3
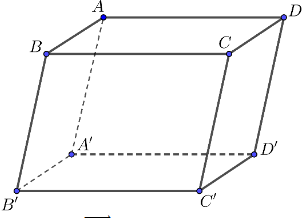
A. \(\overrightarrow {DC} \);
B. \(\overrightarrow {DA} \);
C. \(\overrightarrow {BB'} \);
D. \(\overrightarrow {C'C} \).
Lời giải
Đáp án đúng là: B
Vì BC // DA nên \(\overrightarrow {BC} ,\overrightarrow {DA} \) là hai vectơ cùng phương.
Câu 4
A. \(\overrightarrow {A'B'} \);
B. \(\overrightarrow {CD} \);
C. \(\overrightarrow {BC} \);
D. \(\overrightarrow {AB} \).
Lời giải
Đáp án đúng là: B
Vì \(\overrightarrow {BA} ,\overrightarrow {CD} \) là hai vectơ cùng hướng và BA = CD nên \(\overrightarrow {BA} ,\overrightarrow {CD} \) là hai vectơ bằng nhau.
Câu 5
A. \(\overrightarrow {DC} \);
B. \(\overrightarrow {CD} \);
C. \(\overrightarrow {AD} \);
D. \(\overrightarrow {BC} \).
Lời giải
Đáp án đúng là: A
Vì \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) cùng hướng và AB = DC nên \(\overrightarrow {AB} = \overrightarrow {DC} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\overrightarrow {BI} \);
B. \(\overrightarrow {CD} \);
C. \(\overrightarrow {CI} \);
D. \(\overrightarrow {AB} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
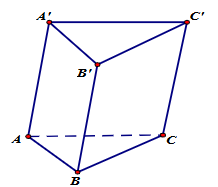
Câu 9
A. \(\overrightarrow {A'C'} \);
B. \(\overrightarrow {BA'} \);
C. \(\overrightarrow {BB'} \);
D. \(\overrightarrow {C'C} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \(\overrightarrow {AB} ;\overrightarrow {CA} ;\overrightarrow {AD} \);
B. \(\overrightarrow {BA} ;\overrightarrow {AC} ;\overrightarrow {AD} \);
C. \(\overrightarrow {AB} ;\overrightarrow {AC} ;\overrightarrow {DA} \);
D. \(\overrightarrow {AB} ;\overrightarrow {AC} ;\overrightarrow {AD} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.