10 bài tập Một số bài toán thực tế ứng dụng giá trị lớn nhất và giá trị nhỏ nhất của hàm có lời giải
44 người thi tuần này 4.6 1 K lượt thi 10 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Câu 1
A. t = 2;
B. t = 1;
C. t = 3;
D. t = 4.
Lời giải
Đáp án đúng là: B
Ta có v(t) = S'(t) = −3t2 + 6t = −3(t2 – 2t + 1) + 3 = −3(t – 1)2 + 3 ≤ 3.
Dấu “=” xảy ra khi t = 1.
Vậy vận tốc của chuyển động đạt giá trị lớn nhất bằng 3 khi t = 1.
Câu 2
A. 243 (m/s);
B. 27 (m/s);
C. 144 (m/s);
D. 36 (m/s).
Lời giải
Đáp án đúng là: D
Ta có: v = s' = −t2 + 12t; v' = −2t + 12; v' = 0 t = 6.
Bảng biến thiên
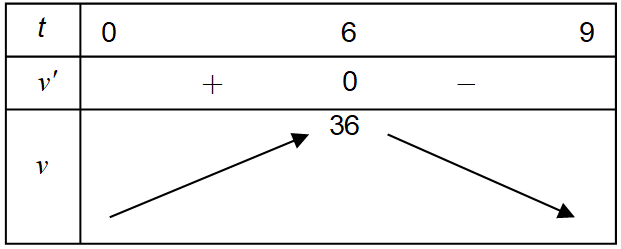
Nhìn bảng biến thiên ta thấy vận tốc đạt giá trị lớn nhất khi t = 6.
Giá trị lớn nhất là v(6) = 36 m/s.
Câu 3
A. 88 m/s;
B. 25 m/s;
C. 100 m/s;
D. 11 m/s.
Lời giải
Đáp án đúng là: B
Ta có v = S' = −t2 + 8t + 9, t ∈ (0; 10).
Có v' = −2t + 8; v' = 0 t = 4 ∈ (0; 10).
Bảng biến thiên:
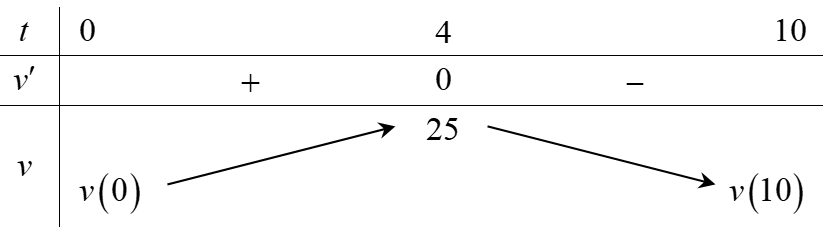
Vậy vận tốc lớn nhất của chất điểm là 25 m/s tại t = 4.
Câu 4
A. \(16\sqrt 3 \) cm;
B. \(4\sqrt 3 \)cm;
C. 24 cm;
D. \(8\sqrt 3 \)cm.
Lời giải
Đáp án đúng là: A
Gọi cạnh của hình chữ nhật: a, b; 0 < a, b  48
48
Ta có: \(ab = 48 \Leftrightarrow b = \frac{{48}}{a}\). Chu vi: \(P\left( a \right) = 2\left( {a + \frac{{48}}{a}} \right)\).
Có \[P'\left( a \right) = 2\left( {1 - \frac{{48}}{{{a^2}}}} \right);P'\left( a \right) = 0 \Leftrightarrow a = 4\sqrt 3 \].
Bảng biến thiên:
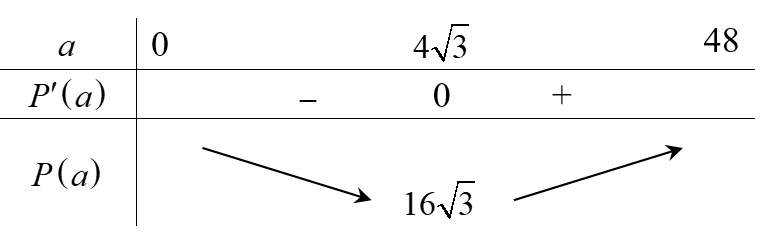
Vậy hình chữ nhật có chu vi nhỏ nhất là \(16\sqrt 3 \).
Câu 5
A. 3 cm;
B. 4 cm;
C. 5 cm;
D. 2 cm.
Lời giải
Đáp án đúng là: A
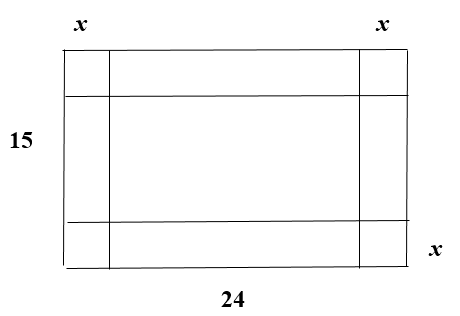
Giả sử độ dài cạnh hình vuông của các miếng tôn bị cắt bỏ bằng
x (\[0 < x < \frac{{15}}{2}\]).
Khi đó hình hộp chữ nhật có chiều cao bằng x, chiều rộng bằng 15 – 2x và chiều dài bằng 24 – 2x.
Suy ra hình hộp chữ nhật có thể tích V = x(15 – 2x)(24 – 2x) = 4x3 – 78x2 + 360x.
Xét hàm f(x) = 4x3 – 78x2 + 360x trên \[\left( {0;\frac{{15}}{2}} \right)\].
Có f'(x) = 12x2 – 156x + 360 = 0 x = 3 hoặc x = 10.
Bảng biến thiên
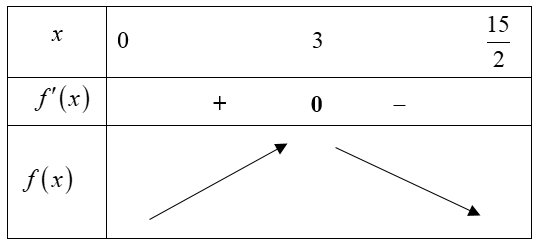
Dựa vào bảng biến thiên ta có hàm số đạt giá trị lớn nhất trên \[\left( {0;\frac{{15}}{2}} \right)\] tại x = 3 hay hình hộp chữ nhật có thể tích lớn nhất khi độ dài cạnh hình vuông của miếng tôn bị cắt bỏ bằng 3 cm.
Câu 6
A. 83200 đồng;
B. 320000 đồng;
C. 832000 đồng;
D. 32000 đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 4 giờ;
B. 1 giờ;
C. 3 giờ;
D. 2 giờ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.