12 bài tập Một số bài toán hàm hợp liên quan đến tính đơn điệu và cực trị có đáp án
341 người thi tuần này 4.6 1.7 K lượt thi 12 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Lời giải
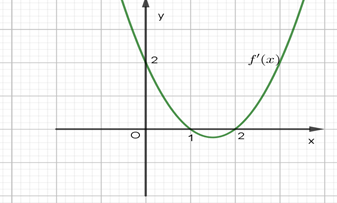
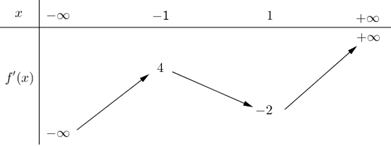
Ta có y' = f'(5 – 2x) = −2f'(5 −2x).
Có y' = 0 Û −2f'(5 – 2x) = 0 Û \(\left[ \begin{array}{l}5 - 2x = - 3\\5 - 2x = - 1\\5 - 2x = 1\end{array} \right.\)Û \(\left[ \begin{array}{l}x = 4\\x = 3\\x = 2\end{array} \right.\).
Ta có f'(5 – 2x) < 0 Û \(\left[ \begin{array}{l}5 - 2x < - 3\\ - 1 < 5 - 2x < 1\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x > 4\\2 < x < 3\end{array} \right.\).
f'(5 – 2x) > 0 Û \(\left[ \begin{array}{l}5 - 2x > 1\\ - 3 < 5 - 2x < - 1\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x < 2\\3 < x < 4\end{array} \right.\).
Bảng biến thiên của hàm số y = f(5 – 2x)
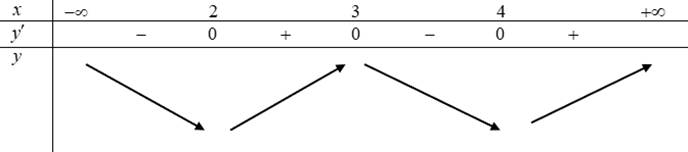
Dựa vào bảng biến thiên ta thấy hàm số y = f(5 – 2x) đồng biến trên khoảng (2; 3) và (4; +∞).
Lời giải
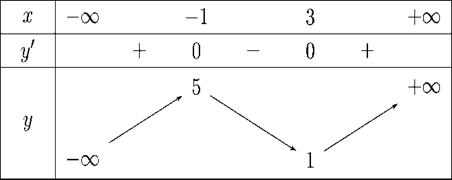
Từ giả thiết, ta có bảng biến thiên của hàm số f(x)

Ta có g'(x) = −f'(3 – x).
Từ bảng biến thiên của hàm số f(x) ta có
g'(x) > 0 f'(3 – x) < 0 \( \Leftrightarrow \left[ \begin{array}{l}3 - x < - 1\\1 < 3 - x < 4\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x > 4\\ - 1 < x < 2\end{array} \right.\).
Như thế ta có bảng biến thiên của hàm số g(x)
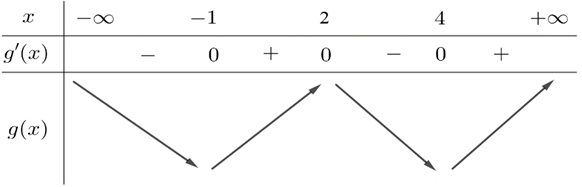
Từ bảng biến thiên, ta nhận thấy hàm số g(x) có 1 điểm cực đại.
Câu 3
A. 1;
B. 2;
C. 3;
Lời giải
Đáp án đúng là: B
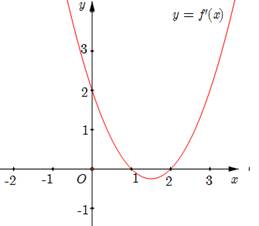
Có y' = −2x.f'(2 – x2).
Có y' > 0 \[ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 0\\1 < 2 - {x^2} < 2\end{array} \right.\\\left\{ \begin{array}{l}x < 0\\\left[ \begin{array}{l}2 - {x^2} < 1\\2 - {x^2} > 2\end{array} \right.\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 0\\ - 1 < x < 1\end{array} \right.\\\left\{ \begin{array}{l}x < 0\\\left[ \begin{array}{l}x < - 1\\x > 1\end{array} \right.\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}0 < x < 1\\x < - 1\end{array} \right.\].
Do đó hàm số đồng biến trên (0; 1). Khi đó a = 0; b = 1 và a + 2b = 2.
Câu 4
A. (1; +∞);
B. \(\left( {\frac{1}{2};1} \right)\);
C. \(\left( {0;\frac{1}{2}} \right)\);
Lời giải
Đáp án đúng là: B
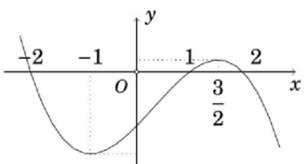
Ta có g'(x) = −2f'(3 – 2x).
Có g'(x) > 0 f'(3 – 2x) < 0 1 < 3 – 2x < 2 \( \Leftrightarrow \frac{1}{2} < x < 1\).
Vậy hàm số đã cho đồng biến trên \(\left( {\frac{1}{2};1} \right)\).
Câu 5
A. (−2; −1);
B. \(\left( { - 1;\frac{3}{2}} \right)\);
C. (−1; 1);
Lời giải
Đáp án đúng là: D
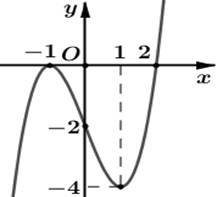
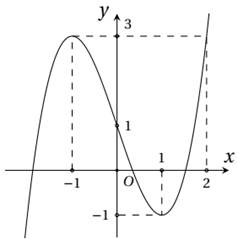
Từ đồ thị hàm số trên, ta có bảng biến thiên như sau:
Þ f(x) < 0,∀x ≠ ±2.
Ta có g'(x) = 2f(x).f'(x).
\[g'\left( x \right) = 2f\left( x \right).f'\left( x \right) < 0 \Leftrightarrow f'\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}1 < x < 2\\x < - 2\end{array} \right.\].
Vậy hàm số đã cho nghịch biến trên khoảng (1; 2).
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Hàm số g(x) nghịch biến trên khoảng (−∞; −2);
B. Hàm số g(x) đồng biến trên khoảng (2; +∞);
C. Hàm số g(x) nghịch biến trên khoảng (−1; 0);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. 3;
B. 2;
C. 4;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. 0;
B. 1;
C. 2;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. 3;
B. 2;
C. 1;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.