Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Bình Phước
109 người thi tuần này 4.6 231 lượt thi 14 câu hỏi 60 phút
🔥 Đề thi HOT:
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
123 bài tập Nón trụ cầu và hình khối có lời giải
Nội dung liên quan:
Danh sách câu hỏi:
Đoạn văn 1
Câu 1-2: (2,0 điểm)
Lời giải
\(A = \sqrt {16} + \sqrt[3]{{27}} = \sqrt {{4^2}} + \sqrt[3]{{{3^3}}} = 4 + 3 = 7.\)
\(B = \sqrt {{{\left( {3 + \sqrt 5 } \right)}^2}} = \left| {3 + \sqrt 5 } \right| = 3 + \sqrt 5 .\)
Lời giải
Với \(x \ne - \sqrt 5 ,\) ta có:
\(P = \frac{{{x^2} - 5}}{{x + \sqrt 5 }} = \frac{{\left( {x + \sqrt 5 } \right)\left( {x - \sqrt 5 } \right)}}{{x + \sqrt 5 }} = x - \sqrt 5 .\)
Vậy với \(x \ne - \sqrt 5 \) thì \(P = x - \sqrt 5 .\)
Đoạn văn 2
Câu 3-5: (2,0 điểm)
Lời giải
\(\left( {2x + 3} \right)\left( {3x - 6} \right) = 0\)
\(2x + 3 = 0\) hoặc \(3x - 6 = 0\)
\(2x = - 3\) hoặc \(3x = 6\)
\(x = - \frac{3}{2}\) hoặc \(x = 2.\)
Vậy phương trình đã cho có nghiệm là \(x = - \frac{3}{2};\,\,x = 2.\)
Câu 4
2) Không sử dụng máy tính hãy giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}5x - 2y = 8\\3x + 4y = 10.\end{array}\end{array}} \right.\)
Lời giải
\(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}5x - 2y = 8\,\,\,\,\,\left( 1 \right)\\3x + 4y = 10\,\,\,\left( 2 \right)\end{array}\end{array}} \right.\)
Nhân hai vế của phương trình (1) với 2, ta được hệ phương trình mới \[\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}10x - 4y = 16\,\,\,\,\,\left( 3 \right)\\3x + 4y = 10\,\,\,\,\,\left( 2 \right)\end{array}\end{array}} \right.\]
Cộng từng vế của hai phương trình của hệ trên, ta được phương trình:
\(13x = 26,\) suy ra \(x = 2.\)
Thay \(x = 2\) vào phương trình (1), ta được: \(5 \cdot 2 - 2y = 8,\) suy ra \(y = 1.\)
Vậy hệ phương trình đã cho có nghiệm là \(\left( {2;\,\,1} \right).\)
Câu 5
3) Một sân bóng đá 7 người có chiều dài lớn hơn chiều rộng 20 m và có diện tích bằng \(1\,\,664\;\,{{\rm{m}}^2}.\) Tính chiều dài và chiều rộng của sân bóng đá đó.
Lời giải
Gọi chiều rộng mảnh vườn hình chữ nhật là \[x\] (m) \[\left( {x > 0} \right).\]
Chiều rộng ngắn hơn chiều dài 6 m nên chiều dài mảnh vườn là \(x + 20\) (m).
Diện tích mảnh vườn là: \(x\left( {x + 20} \right)\) (m2).
Theo bài, mảnh vườn có diện tích là \(1\,\,664\) m2 nên ta có phương trình:
\(x\left( {x + 20} \right) = 1\,\,664\)
\({x^2} + 20x - 1\,\,664 = 0.\)
Ta có \(\Delta ' = {10^2} - 1 \cdot \left( { - 1\,\,664} \right) = 1\,\,764 > 0\) và \(\sqrt {1\,\,764} = 42.\)
Do đó, phương trình có hai nghiệm phân biệt:
\[{x_1} = --10 + 42 = 32,{\rm{ }}{x_2} = --10--42 = --52.\]
Ta thấy chỉ có giá trị \[{x_1} = 32\] thỏa mãn điều kiện \[x > 0.\]
Vậy chiều rộng mảnh vườn là \(32\) m và chiều dài mảnh vườn là \[32 + 20 = 52\] (m).
Đoạn văn 3
Câu 6-7: (2,0 điểm)
Lời giải
Bảng giá trị của hàm số:
|
\(x\) |
\( - 2\) |
\( - 1\) |
\(0\) |
\(1\) |
\(2\) |
|
\(y = \frac{1}{2}{x^2}\) |
\(2\) |
\(\frac{1}{2}\) |
\(0\) |
\(\frac{1}{2}\) |
\(2\) |
Trên mặt phẳng tọa độ \(Oxy,\) lấy các điểm \(A\left( { - 2;\,\,2} \right),\) \(B\left( { - 1;\,\,\frac{1}{2}} \right),\) \(O\left( {0;\,\,0} \right),\) \(C\left( {1;\,\,\frac{1}{2}} \right),\) \(D\left( {2;\,\,2} \right).\)
Đồ thị của hàm số \(y = \frac{1}{2}{x^2}\) là một đường parabol đỉnh \(O,\) đi qua các điểm trên và có dạng như hình vẽ sau:
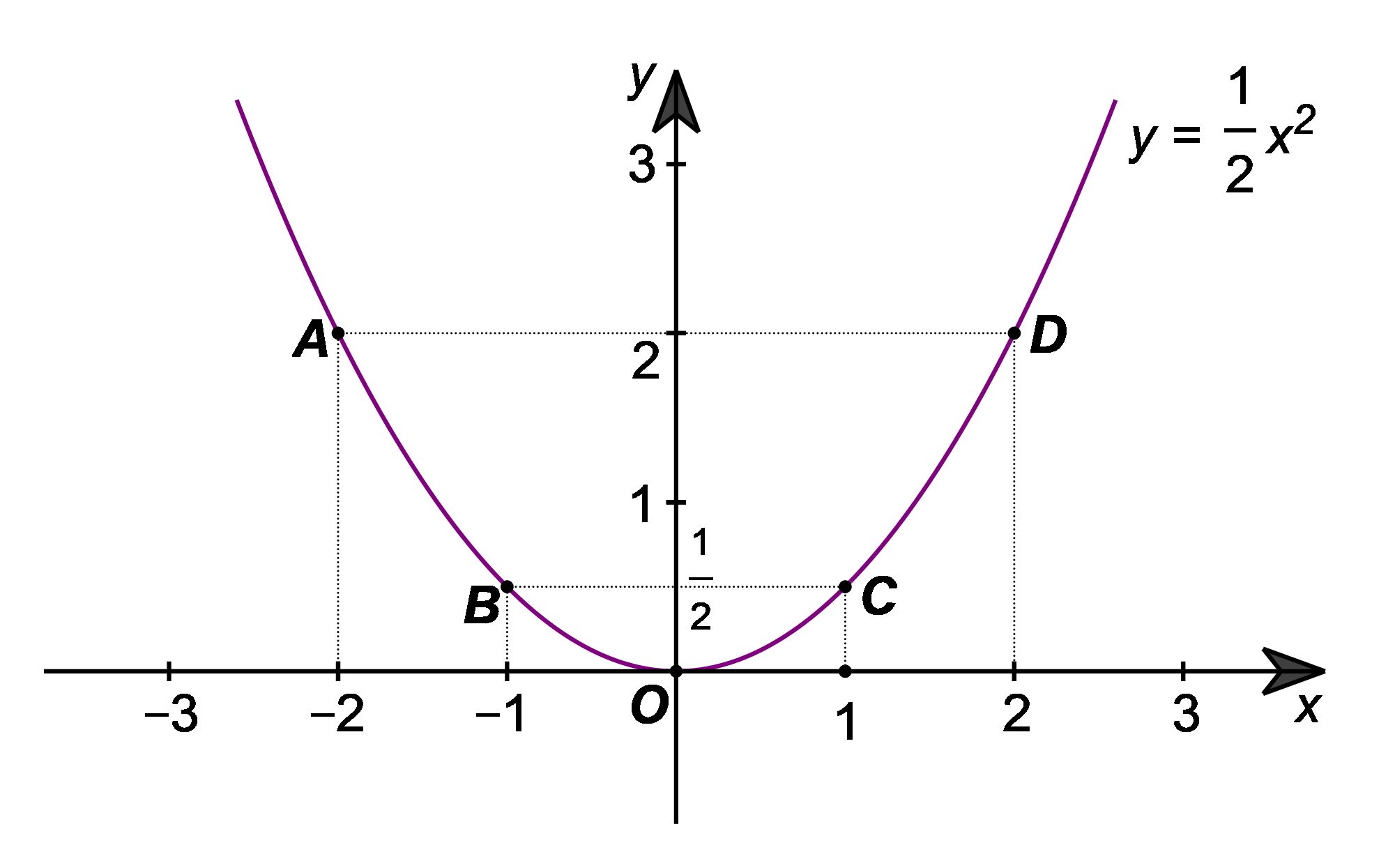
Câu 7
2) Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình: \({x^2} - 2x - 5 = 0.\) Không giải phương trình, tính giá trị của biểu thức \(S = x_1^3 + 9{x_2} + 7.\)
Lời giải
Vì \({x_1}\) là nghiệm của phương trình \({x^2} - 2x - 5 = 0\) nên ta có \(x_1^2 - 2{x_1} - 5 = 0,\) suy ra \(x_1^2 = 2{x_1} + 5.\)
Theo định lí Viète, ta có: \({x_1} + {x_2} = 2.\)
Ta có: \(S = x_1^3 + 9{x_2} + 7 = {x_1} \cdot x_1^2 + 9{x_2} + 7 = {x_1} \cdot \left( {2{x_1} + 5} \right) + 9{x_2} + 7\)
\( = 2x_1^2 + 5{x_1} + 9{x_2} + 7 = 2 \cdot \left( {2{x_1} + 5} \right) + 5{x_1} + 9{x_2} + 7 = 4{x_1} + 10 + 5{x_1} + 9{x_2} + 7\)
\( = 9{x_1} + 9{x_2} + 17 = 9\left( {{x_1} + {x_2}} \right) + 17 = 9 \cdot 2 + 17 = 35.\)
Vậy giá trị của biểu thức \(S\) là \(35.\)
Đoạn văn 4
Câu 8-9: (1,0 điểm) Sau bài thi môn Ngữ văn, cô giáo ghi lại số lỗi chính tả của 40 học sinh trong lớp 9A vào bảng thống kê sau:
\[\begin{array}{*{20}{l}}{\;2}&{\;5}&{\;2}&{\;2}&{\;1}&{\;3}&{\;4}&{\;0}&{\;5}&{\;2}&{\;5}&{\;1}&{\;2}&{\;1}&{\;3}&{\;5}&{\;1}&{\;0}&{\;4}&{\;1}\\{\;4}&{\;2}&{\;1}&{\;4}&{\;3}&{\;3}&{\;2}&{\;0}&{\;4}&{\;5}&{\;4}&{\;5}&{\;1}&{\;4}&{\;1}&{\;1}&{\;0}&{\;3}&{\;1}&{\;4}\end{array}\]
Lời giải
Bảng tần số biểu diễn số lỗi chính tả của học sinh như sau:
|
Số lỗi chính tả |
0 |
1 |
2 |
3 |
4 |
5 |
|
Tần số |
4 |
10 |
7 |
5 |
8 |
6 |
Kích thước mẫu là: \(N = 40.\)
Vì tần số của giá trị 0 là 4 nên tần số tương đối của giá trị 0 là\(\frac{4}{{40}} \cdot 100\% = 10\% .\)
Vì tần số của giá trị 1 là 10 nên tần số tương đối của giá trị 1 là \(\frac{{10}}{{40}} \cdot 100\% = 25\% .\)
Tương tự, ta tính được tần số tương đối của các giá trị 2, 3, 4, 5 lần lượt là \(17,5\% ;\,\,12,5\% ;\,\,20\% ;\,\,15\% .\)
Ta thu được bảng tần số tương đối như sau:
|
Số lỗi chính tả |
0 |
1 |
2 |
3 |
4 |
5 |
|
Tần số tương đối |
\(10\% \) |
\(25\% \) |
\(17,5\% \) |
\(12,5\% \) |
\(20\% \) |
\(15\% \) |
Câu 9
2) Lấy ngẫu nhiên một học sinh trong lớp 9A, tính xác suất để học sinh này có số lỗi nhiều hơn 3.
Lời giải
2) Khi chọn ngẫu nhiên một học sinh trong lớp 9A, các kết quả là đồng khả năng.
Có tất cả 40 kết quả xảy ra và số kết quả thuận lợi để học sinh này có số lỗi nhiều hơn 3 là: \(8 + 6 = 14.\)
Xác suất để học sinh này có số lỗi nhiều hơn 3 là: \(\frac{{14}}{{40}} = \frac{7}{{20}}.\)
Đoạn văn 5
Câu 10-11: (1,5 điểm)
Câu 10
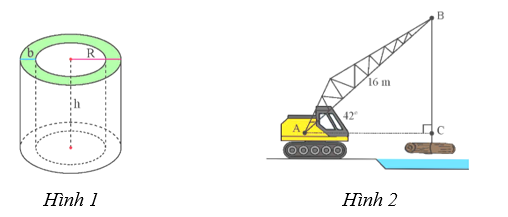
1) Một bể nước hình trụ có bán kính đáy \(R = 1,2\;\;{\rm{m}}\) (tính từ tâm bể đến mép ngoài), bề dày của thành bể là \(b = 0,05\;\;{\rm{m,}}\) chiều cao lòng bể là \(h = 1,6\;\;{\rm{m}}\) (Hình 1). Tính dung tích của bể nước (kết quả làm tròn đến hàng phần trăm).

Lời giải
Bán kính của lòng bể là: \(r = R - b = 1,2 - 0,05 = 1,15{\rm{\;(m)}}{\rm{.}}\)
Dung tích của bể nước là: \(V = \pi {r^2}h = \pi \cdot 1,{15^2} \cdot 1,6 = 2,116\pi {\rm{\;(}}{{\rm{m}}^3}{\rm{)}} \approx 6,65{\rm{\;(}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\)
Câu 11
2) Một cần cẩu đang nâng một khối gỗ trên sông. Biết tay cẩu \(AB\) có chiều dài 16 m và nghiêng một góc \(42^\circ \) so với phương nằm ngang (Hình 2). Tính chiều dài \[BC\] của đoạn dây cáp (kết quả làm tròn đến hàng phần trăm).
Lời giải
Xét \(\Delta ABC\) vuông tại \(C,\) ta có: \[BC = AC \cdot \sin A = 16 \cdot \sin 42^\circ \approx 10,71{\rm{\;(m)}}{\rm{.}}\]
Vậy chiều dài \(BC\) của đoạn dây cáp khoảng \[10,71{\rm{\;m}}.\]
Đoạn văn 6
Câu 12-14: (1,5 điểm) Cho tam giác nhọn \(ABC\) hai đường cao \(BE,\,\,CF\) cắt nhau tại \(H.\) Gọi \(M\) là trung điểm của \(BC,\,\,I\) là trung điểm của \(AH.\)
Lời giải

Xét \(\Delta AEH\) vuông tại \(E\) có \(I\) là trung điểm của cạnh huyền \(AH\) nên đường tròn ngoại tiếp \(\Delta AEH\) là đường tròn tâm \(I\) đường kính \(AH.\)
Tương tự, đường tròn ngoại tiếp \(\Delta AFH\) vuông tại \(F\) là đường tròn tâm \(I\) đường kính \(AH.\)
Như vậy, đường tròn tâm \(I\) đường kính \(AH\) đi qua các điểm \(A,\,\,E,\,\,H,\,\,F.\)
Vậy tứ giác \(AEHF\) nội tiếp đường tròn tâm \(I.\)
Lời giải
Ta có \(IA = IF\) nên \(\Delta IAF\) cân tại \(I.\) Suy ra \(\widehat {IAF} = \widehat {IFA}.\) (1)
Vì tứ giác \(AEHF\) là tứ giác nội tiếp nên \(\widehat {HAF} = \widehat {HEF}\) (hai góc nội tiếp cùng chắn cung \(HF).\) (2)
Chứng minh tương tự câu 1, ta cũng có tứ giác \[BFEC\] nội tiếp đường tròn tâm \(M\) đường kính \(FC.\)
Do đó \[\widehat {BEF} = \widehat {BCF}\] (hai góc nội tiếp cùng chắn cung \(BF).\) (3)
Ta có \(MF = MC\) nên \(\Delta MFC\) cân tại \(M.\) Suy ra \(\widehat {MCF} = \widehat {MFC}.\) (4)
Từ (1), (2), (3) và (4) suy ra \(\widehat {IFA} = \widehat {MFC}.\)
Lại có \(\widehat {IFA} + \widehat {IFC} = 90^\circ \) suy ra \(\widehat {MFC} + \widehat {IFC} = 90^\circ \) hay \(\widehat {IFM} = 90^\circ \) nên \(FM \bot FI.\)
Câu 14
3) Tiếp tuyến tại các điểm \(B\) và \(C\) của đường tròn ngoại tiếp tam giác \(ABC\) cắt nhau tại điểm \(N.\) Chứng minh rằng \(AN\) đi qua trung điểm của đoạn thẳng \(EF.\)
Lời giải
⦁ Do tứ giác \(BFEC\) nội tiếp đường tròn nên \(\widehat {BFE} + \widehat {BCE} = 180^\circ \) (tổng hai góc đối nhau của tứ giác nội tiếp).
Mà \(\widehat {BFE} + \widehat {AFE} = 180^\circ \) (hai góc kề bù) nên \[\widehat {AFE} = \widehat {BCE}.\]
Xét \(\Delta AEF\) và \(\Delta ABC\) có: \(\widehat {BAC}\) là góc chung và \(\widehat {AFE} = \widehat {ACB}.\)
Do đó (g.g). Suy ra \(\frac{{AF}}{{AC}} = \frac{{EF}}{{BC}}.\)
Gọi \(P\) là trung điểm của \(EF.\) Khi đó, \(EF = 2FP.\)
Do \(M\) là trung điểm của \(BC\) nên \(BC = 2CM.\)
Do đó \(\frac{{AF}}{{AC}} = \frac{{EF}}{{BC}} = \frac{{2FP}}{{2CM}} = \frac{{FP}}{{CM}}.\)
Xét \(\Delta AFP\) và \(\Delta ACM\) có: \(\widehat {AFP} = \widehat {ACM}\) và \(\frac{{AF}}{{AC}} = \frac{{FP}}{{CM}}.\)
Do đó (c.g.c). Suy ra \(\widehat {FAP} = \widehat {CAM}\) (hai góc tương ứng). (9)
⦁ Gọi \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC.\)
Vì \(NB,\,\,NC\) là hai tiếp tuyến của đường tròn \(\left( O \right)\) nên \(NB = NC\) (tính chất hai tiếp tuyến cắt nhau), suy ra \(N\) nằm trên đường trung trực của \(BC.\)
Lại có \(OB = OC\) nên \(O\) nằm trên đường trung trực của \(BC.\)
Do đó \(ON\) là đường trung trực của \(BC.\)
Mà \(M\) là trung điểm của \(BC\) nên đường trung trực \[ON\] của \(BC\) đi qua \(M\) hay \(ON \bot BC\) tại \(M.\)
Xét \(\Delta ABC\) có hai đường cao \(BE,\,\,CF\) cắt nhau tại \(H\) nên \(H\) là trực tâm của tam giác, suy ra \(AH \bot BC.\)
Ta có \(ON \bot BC\) và \(AH \bot BC\) nên \(ON\,{\rm{//}}\,AH.\) Suy ra \(\widehat {HAN} = \widehat {ONA}\) (hai góc so le trong). (5)
Xét \(\Delta OBM\) và \(\Delta ONB\) có: \(\widehat {OMB} = \widehat {OBN} = 90^\circ \) và \(\widehat {BON}\) là góc chung
Do đó (g.g). Suy ra \(\frac{{OB}}{{ON}} = \frac{{OM}}{{OB}}\) hay \(O{B^2} = OM \cdot ON.\)
Mà \(OB = OA\) nên \(O{A^2} = OM \cdot ON,\) suy ra \(\frac{{OA}}{{OM}} = \frac{{ON}}{{OA}}.\)
Xét \(\Delta ONA\) và \(\Delta OAM\) có: \(\widehat {AON}\) là góc chung và \(\frac{{OA}}{{OM}} = \frac{{ON}}{{OA}}.\)
Do đó (g.g). Suy ra \(\widehat {ONA} = \widehat {OAM}\) (hai góc tương ứng). (6)
Từ (5) và (6) suy ra \(\widehat {HAN} = \widehat {OAM}.\) (7)
Xét \(\Delta OAC\) cân tại \(O\) (do \(OA = OC)\) nên \(\widehat {OAC} = \widehat {OCA} = \frac{{180^\circ - \widehat {AOC}}}{2}.\)
Lại có \(\widehat {ABC},\,\,\widehat {AOC}\) lần lượt là góc nội tiếp, góc ở tâm cùng chắn cung \(AC\) của đường tròn \(\left( O \right)\) nên \(\widehat {ABC} = \frac{1}{2}\widehat {AOC}\) hay \(\widehat {AOC} = 2\widehat {ABC}.\)
Do đó \(\widehat {OAC} = \frac{{180^\circ - 2\widehat {ABC}}}{2} = 90^\circ - \widehat {ABC} = 90^\circ - \widehat {FBC}.\)
Mà \(\widehat {FBC} + \widehat {FCB} = 90^\circ \) (tổng hai góc nhọn của \(\Delta FBC\) vuông tại \(F)\) nên \(\widehat {FCB} = 90^\circ - \widehat {FBC}.\)
Suy ra \(\widehat {OAC} = \widehat {FCB}.\)
Mặt khác, \(\widehat {HAF} = \widehat {HEF}\) và \[\widehat {BEF} = \widehat {BCF}\] (chứng minh câu 2) nên \(\widehat {HAF} = \widehat {OAC}.\) (8)
Từ (7) và (8) suy ra \(\widehat {HAN} + \widehat {HAF} = \widehat {OAM} + \widehat {OAC}\) hay \(\widehat {FAN} = \widehat {CAM}.\) (10)
⦁ Từ (9) và (10) suy ra \(\widehat {FAP} = \widehat {FAN}\) hay ba điểm \(A,\,\,P,\,\,N\) thẳng hàng.
Vậy đường thẳng \(AN\) đi qua trung điểm \(P\) của \(EF.\)
46 Đánh giá
50%
40%
0%
0%
0%