Ôn thi Cấp tốc 789+ vào 10 môn Toán khu vực TP Hồ Chí Minh 2024 - 2025 (Đề 13)
42 người thi tuần này 4.6 1.1 K lượt thi 8 câu hỏi 50 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
a) Vẽ \(\left( P \right)\) và \(\left( d \right)\) trên cùng hệ trục tọa độ.
|
\(x\) |
\( - 2\) |
\( - 1\) |
0 |
1 |
2 |
|
\(y = - {x^2}\) |
\( - 4\) |
\( - 1\) |
0 |
\( - 1\) |
\( - 4\) |
Do đó, đồ thị hàm số là đường cong đi qua các điểm \(O\left( {0\,;\,\,0} \right);\,\,A\left( { - 2\,;\,\, - 4} \right);\,\,\)\(B\left( { - 1\,;\,\, - 1} \right);\)
\(C\left( {1\,;\,\, - 1} \right);\) \(\,D\left( {2\,;\,\, - 4} \right).\)
* Vẽ \(\left( d \right)\): Ta có bảng giá trị:
|
\(x\) |
0 |
1 |
|
\(y = - 3x + 2\) |
2 |
\( - 1\) |
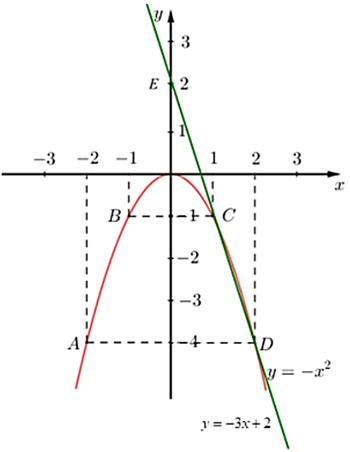
b) Phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là
\( - {x^2} = 3x + 2\)
\( - {x^2} + 3x - 2 = 0\)
\(x = 1\) hoặc \(x = 2\)
Với \(x = 1\) thì \(y = - 1\);
Với \(x = 2\) thì \(y = - 4\).
Vậy tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là \(\left( {1\,;\,\, - 1} \right)\) và \(\left( {2\,;\, - 4} \right)\).
Lời giải
Phương trình có hai nghiệm là \({x_1},\,\,{x_2}\) nên áp dụng định lí Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a} = \frac{4}{3}\\{x_1}{x_2} = \frac{c}{a} = \frac{{ - 2}}{3}\end{array} \right.\,\,\left( 1 \right)\)
Ta có \[A = {x_1}x_2^2 + {x_2}\left( {x_1^2 + 2} \right) + 2{x_1} = {x_1}x_2^2 + {x_2}x_1^2 + 2{x_2} + 2{x_1}\]
\[ = {x_1}{x_2}\left( {{x_1} + {x_2}} \right) + 2\left( {{x_1} + {x_2}} \right) = \left( {{x_1}{x_2} + 2} \right)\left( {{x_1} + {x_2}} \right).\]
Thay \(\left( 1 \right)\) vào biểu thức \(A,\) ta có \[A = \left( {\frac{{ - 2}}{3} + 2} \right) \cdot \frac{4}{3} = \frac{{16}}{9}.\] Vậy \[A = \frac{{16}}{9}.\]
Lời giải
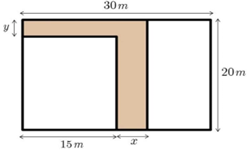
a) Gọi các phần còn lại lần lượt là \(A\) và \(B\) (như hình vẽ).
Biểu thức biểu thị cạnh còn thiếu của \(A\) là: \(20 - y.\)
Biểu thức biểu thị diện tích phần \(A\) là:
\({S_A} = 15\left( {20 - y} \right) = 300 - 15y.\)
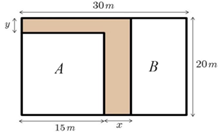
Biểu thức biểu thị cạnh còn thiếu của \(B\) là: \(30 - 15 - x = 15 - x.\)
Biểu thức biểu thị diện tích phần \(B\) là: \({S_B} = 20\left( {15 - x} \right) = 300 - 20x.\)
Vậy biểu thức là \(15\left( {20 - y} \right) + 20\left( {15 - x} \right) = 600 - 20x - 15y\).
b) Thay \(x = 2,4\) và \(y = 1,8\) vào \(S,\) ta được:
\(S = 600 - 20 \cdot 2,4 - 15 \cdot 1,8 = 525\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Vậy diện tích phần còn lại của khu vườn là \(525\,\,{{\rm{m}}^{\rm{2}}}.\)
Lời giải
Số tiền anh Tâm phải trả khi thuê pin gói linh hoạt là:
\(189\,\,000 + 374\left( {800 - 400} \right) = 338\,\,600\) (đồng)
Do đó nếu sử dụng gói linh hoạt thì anh Tâm sẽ tiết kiệm được:
\(350\,\,000 - 338\,\,600 = 11400\) (đồng).
Vậy anh Tâm nên sử dụng gói linh hoạt.
Lời giải
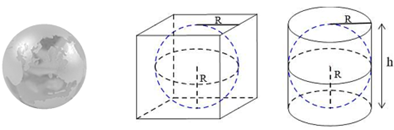
a) Ta có: \(V = \frac{4}{3}\pi {R^3}\) nên \[R = \sqrt[3]{{\frac{{3V}}{{4\pi }}}} = \sqrt[3]{{\frac{{3 \cdot 4,2}}{{4\pi }}}} \approx 1\,\,\left( {{\rm{dm}}} \right).\]
Vậy bán kính của mô hình Trái đất mà anh Huy thiết kế khoảng \[1\,\,{\rm{dm}}.\]
b) Vì các mặt hộp đều tiếp xúc với mô hình Trái đất nên bán kính của hình trụ sẽ bằng bán kính hình cầu \(R = 1\) và chiều cao \(h = 2R = 2\,\,{\rm{dm}}{\rm{.}}\)
Diện tích các mặt của hình trụ là: \(S = 2\pi Rh + 2\pi {R^2} = 2\pi \cdot 1 \cdot 2 + 2\pi \cdot {1^2} = 6\pi \,\,\left( {{\rm{d}}{{\rm{m}}^{\rm{2}}}} \right).\)
Ta có hình lập phương có cạnh bằng \(2R = 2\,\,{\rm{dm}}\,{\rm{.}}\)
Diện tích các mặt của hình lập phương là: \(S' = 6 \cdot {2^2} = 24\,\,\left( {{\rm{d}}{{\rm{m}}^{\rm{2}}}} \right).\)
Ta thấy \(24\,\,{\rm{d}}{{\rm{m}}^{\rm{2}}} > 6\pi \,\,{\rm{d}}{{\rm{m}}^{\rm{2}}}\), do đó nếu làm hộp hình trụ sẽ tốn ít giấy hơn.
Vậy anh Huy nên chọn phương án làm hộp hình trụ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.