Đề cương ôn tập cuối kì 1 Toán 12 Chân trời sáng tạo (có tự luận) có đáp án - Bài 4. Khảo sát và vẽ đồ thị một số hàm số cơ bản
25 người thi tuần này 4.6 836 lượt thi 11 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
A. \(y = - {x^3} + 3{x^2} - 3\).
Lời giải
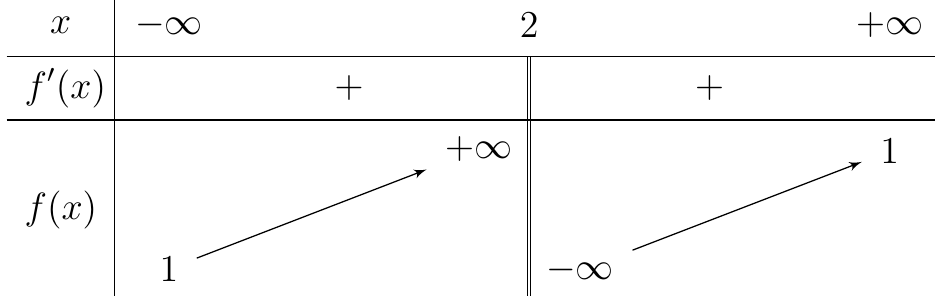
Xét hàm số \(y = {x^3} - 3{x^2} + 2\).
Ta có: \(a = 1 > 0\,;\,\,y' = 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 2\\x = 2 \Rightarrow y = - 2\end{array} \right.\). Chọn D.
Câu 2
A. \[S = 0.\]
Lời giải
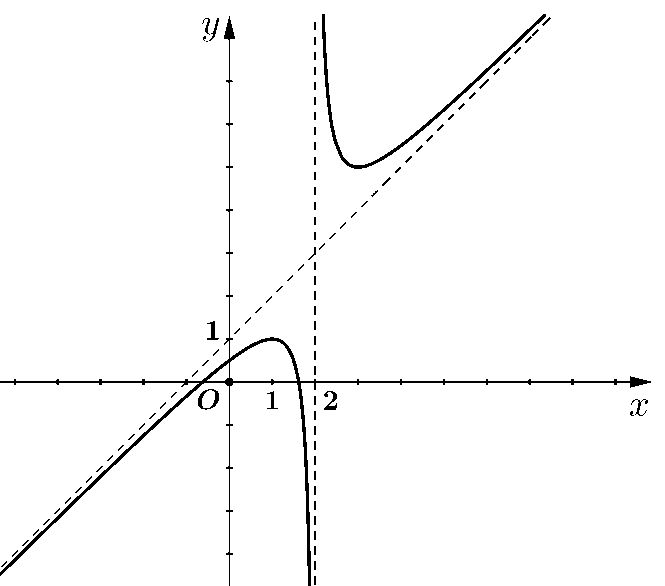
Tiệm cận ngang: \[y = \frac{a}{c} = - 1\]; tiệm cận đứng: \[x = \frac{1}{c} = 1\].
Từ đây suy ra: \[\left\{ \begin{array}{l}a = - 1\\c = 1\end{array} \right.\] mà đồ thị lại cắt trục hoành tại \[x = 2\] nên \[2a + b = 0\] hay \[b = - 2a = 2.\]
Vậy \[S = a + b + c = - 1 + 2 + 1 = 2.\] Chọn C.
Câu 3
Lời giải
Dựa vào đồ thị hàm số ta có tiệm cận đứng của đồ thị hàm số là \(x = 2\) và tiệm cận xiên của đồ thị hàm số là \(y = x + 1\).
+) Xét hàm số \[y = \frac{{{x^2} - x - 1}}{{x - 2}} = x + 1 + \frac{1}{{x - 2}}\] nhận \(y = x + 1\) là tiệm cận xiên của đồ thị hàm số.
Hàm số đó là \[y = \frac{{{x^2} - x - 1}}{{x - 2}}\]. Chọn A.
Lời giải
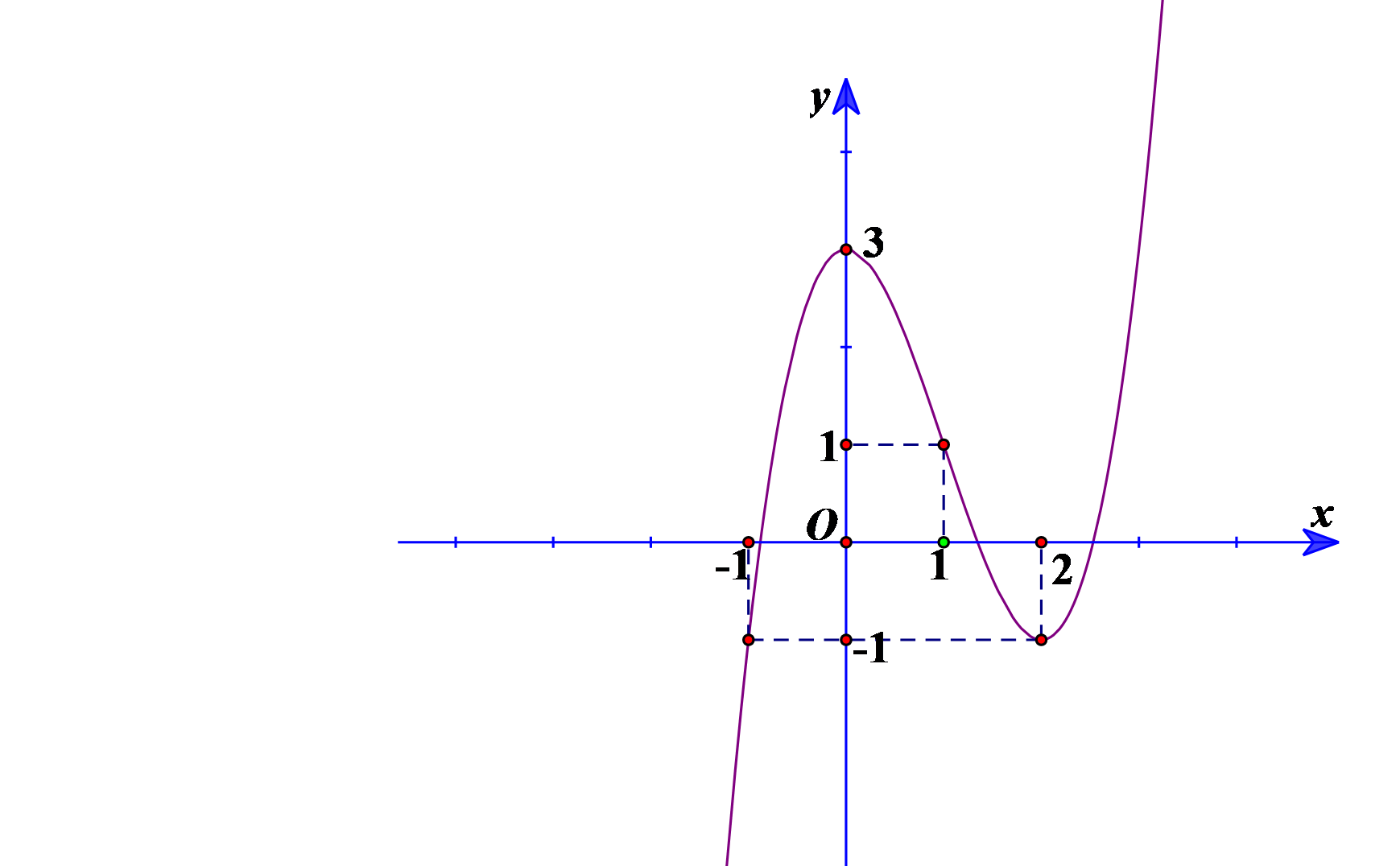
Do \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty \Rightarrow a > 0\) \( \Rightarrow \) phát biểu \(a = - 1\) : Sai
Do \(y(0) = d = 1 > 0\) \( \Rightarrow \) phát biểu \(d = - 1\) và phát biểu \(ad < 0\) đều Sai.
Do \(y( - 1) = 0 \Rightarrow - a + b - c + d = 0 \Rightarrow a + c = b + d = b + 1\) (Đúng), Phát biểu \(ad > 0\) đúng
Vậy các phát biểu 1, 2, 4 sai\( \Rightarrow \) có 3 phát biểu sai. Chọn B.
Câu 5
Lời giải
Đồ thị hàm số \(y = \frac{{a\,x - 1}}{{c\,x + d}}\) có tiệm cận đứng \(x = - \frac{d}{c}\), tiệm cận ngang \(y = \frac{a}{c}\)
Theo đề bài ta có . Chọn B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số \[y = \frac{{ax + b}}{{cx - 1}}\] có đồ thị như hình vẽ bên dưới. Giá trị của tổng \[S = a + b + c\] bằng: A. \[S = 0.\] B. \[S = - 2.\] C. \[S = 2.\] D. \[S = 4.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/5-1761390678.png)
![Đường cong hình bên là đồ thị hàm số \(y = {\rm{a}}{x^3} + b{x^2} + cx + d\). Xét các phát biểu sau: 1. \(a = - 1\) 2. \(ad < 0\) 3. \(ad > 0\) 4. \(d = - 1\) 5.\(a + c = b + 1\) Số phát biểu sai là: A. \[2\]. B. \[3\]. C. \[1\]. D. \[4\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/7-1761390753.png)