11 Bài tập Tìm giao tuyến của hai mặt phẳng (có lời giải)

88 người thi tuần này 4.6 597 lượt thi 11 câu hỏi 45 phút

Câu 1

Cho tứ diện ABCD. M và N là trung điểm của AD và AC. G là trọng tâm tam giác BCD. Giao tuyến của 2 mặt phẳng (GMN) và (BCD) là đường thẳng

A. qua M và song song với AB;

B. qua N và song song với BD;

C. qua G và song song với CD;

D. qua G và song song với BC.

Lời giải

Đáp án đúng là: C

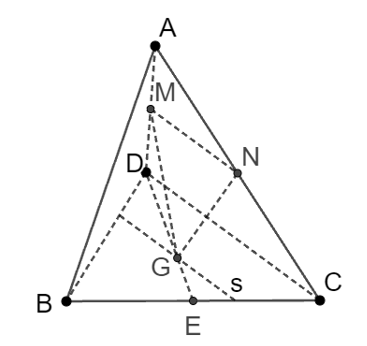
Cho tứ diện ABCD. M và N là trung điểm của AD và AC. G là trọng tâm tam giác BCD. Giao tuyến của 2 mặt phẳng (GMN) và (BCD) là đường thẳng (ảnh 1)

Ta có: $\{\begin{matrix} M N ∥ C D \\ M N \subset (G M N); C D \subset (B C D) \\ (B C D) \cap (G M N) = G \end{matrix}$

$\Rightarrow (G M N) \cap (B C D) = G s ∥ C D ∥ M N$ .

Đáp án đúng là C

Câu 2

Cho hình chóp S. ABCD có đáy là hình thang với các cạnh đáy là AB và CD. M và N là trung điểm AD và BC. G là trọng tâm tam giác SAB. Giao tuyến của (SAB) và (MNG) là:

A. SC;

B. Đường thẳng qua S và song song với AB;

C. Đường thẳng qua G và song song với CD;

D. Đường thẳng qua G và cắt BC.

Lời giải

Đáp án đúng là: C

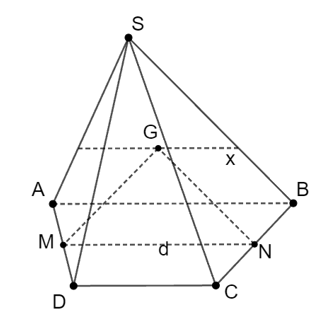
Cho hình chóp S. ABCD có đáy là hình thang với các cạnh đáy là AB và CD. M và N là trung điểm AD và BC. (ảnh 1)

Vì M và N lần lượt là trung điểm của AD và BC.

Nên MN là đường trung bình của hình thang ABCD.

Do đó MN // AB // CD.

Ta có: $\{\begin{matrix} M N ∥ A B \\ M N \subset (G M N); A B \subset (S A B) \\ G \in (S A B) \cap (G M N) \end{matrix}$

Suy ra (GMN) ∩ (SAB) = Gx // MN // AB.

Câu 3

Cho hình bình hành ABCD và điểm S nằm ngoài (ABCD). E là một điểm bất kì thuộc cạnh SA. Giao tuyến của mặt phẳng (ECD) và (SAB) là

A. Qua E và song song với AD;

B. Qua E và song song với AB;

C. Qua E và song song với AC;

D. Qua E và song song với BD.

Lời giải

Đáp án đúng là: B

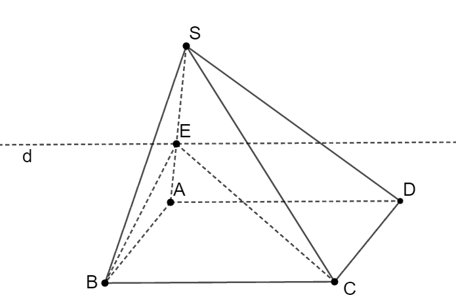
Cho hình bình hành ABCD và điểm S nằm ngoài (ABCD). E là một điểm bất kì thuộc cạnh SA. Giao tuyến của mặt phẳng (ECD) và (SAB) là (ảnh 1)

Ta có: $\{\begin{matrix} C D ∥ A B \\ C D \subset (E C D); A B \subset (S A B) \\ M \in (S A B) \cap (E C D) \end{matrix}$

Do đó (SAB) ∩ (SCD) = d, với d // AB // CD và E ∈ d.

Câu 4

Cho hình thoi ABCD và S nằm ngoài (ABCD). O là giao điểm của AC và BD. E và F lần lượt là trung điểm của CD và AE. Giao tuyến của (SFO) và (SCD) là

A. Qua A và song song EC;

B. Qua E và song song FO;

C. Qua S và song song FO;

D. Qua O và song song EC.

Lời giải

Đáp án đúng là: C

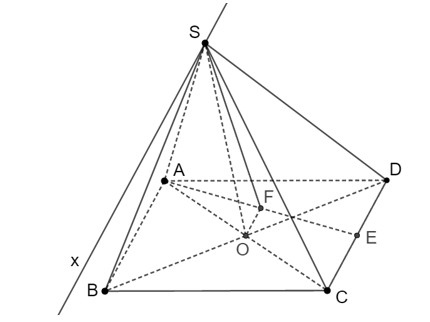
Cho hình thoi ABCD và S nằm ngoài (ABCD). O là giao điểm của AC và BD. (ảnh 1)

Vì F và O là trung điểm của AE và AC nên FO là đường trung bình của tam giác ACE.

Suy ra FO // EC.

Ta có: $\{\begin{matrix} F O ∥ E C \\ F O \subset (S F O); E C \subset (S E C) \\ S \in (S F O) \cap (S E C) \end{matrix}$ .

Do đó (SFO) ∩ (SEC) = Sx // FO // EC.

Câu 5

Cho hình thoi ABCD và S nằm ngoài (ABCD). Lấy điểm E trên SA sao cho 2SE = EA; Lấy điểm F trên SB sao cho 2SF = FB. Điểm H nằm trên cạnh SC không trùng với S. Giao tuyến của (EFH) và (SCD) là

A. Qua A và song song AB;

B. Qua F và song song CD;

C. Qua H và song song CD;

D. Đáp án khác.

Lời giải

Đáp án đúng là: C

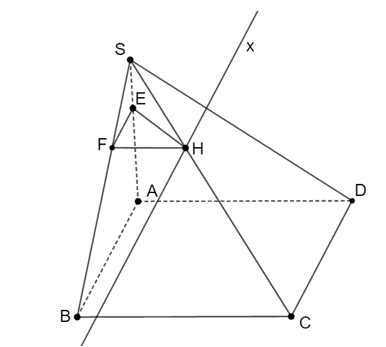
Cho hình thoi ABCD và S nằm ngoài (ABCD). Lấy điểm E trên SA sao cho 2SE = EA; Lấy điểm F trên SB sao cho 2SF = FB (ảnh 1)

Ta có: 2SE = EA và 2SF = FB nên $\frac{S E}{E A} = \frac{S F}{F B} = \frac{1}{2}$ .

Suy ra EF // AB (định lí Thalès đảo) (1)

Lại có ABCD là hình thoi nên AB // CD (2)

Từ (1) và (2) suy ra: EF // CD.

Ta có: $\{\begin{matrix} E F ∥ C D \\ E F \subset (E F H); C D \subset (S C D) \\ H \in (E F H) \cap (S C D) \end{matrix}$ .

Suy ra (EFH) ∩ (SCD) = Hx // EF // CD.

Câu 6

Cho tứ diện ABCD và ba điểm P, Q, R lần lượt trên cạnh AB, CD và BC. Biết rằng PR // AC. Giao điểm S của mp(PQR) và cạnh AD là

A. giao điểm của đường thẳng Qx và AD với Qx // AC;

B. giao điểm của đường thẳng Px và AD với Px // BD;

C. giao điểm của đường thẳng Rx và AD với Rx // BD;

D. giao điểm của đường thẳng Qx và AD với Qx // BD.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hình bình hành ABCD và S nằm ngoài (ABCD). Giao tuyến của hai mặt phẳng (SAB) và (SCD) là

A. Đường thẳng đi qua S song song với AB, CD;

B. Đường thẳng đi qua S;

C. Điểm S;

D. Mặt phẳng (SAD).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Cho hình bình hành ABCD và S nằm ngoài (ABCD). Giao tuyến của hai mặt phẳng (SAB) và (SCD) là một đường thẳng song song với đường thẳng

A. AB;

B. AC;

C. BC;

D. SA.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Cho tứ diện ABCD. Gọi M và N theo thứ tự là trung điểm của AD và AC, G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GMN) và (BCD) là đường thẳng

A. qua M và song song với AB;

B. qua N và song song với BD;

C. qua G và song song với CD;

D. qua G và song song với BC.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Cho hình bình hành ABCD và S nằm ngoài (ABCD), O là giao điểm của AC và BD. M là trung điểm cạnh SC. Trong các khẳng định sau, khẳng định sai là

A. MO // SA;

B. 4 điểm M, O, S và A đồng phẳng;

C. Giao tuyến của (SAB) và (MBD) là Bx trong đó Bx // SA // MO;

D. (MBD) ∩ (SAC) = MD.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Các đường chéo của hình hộp

A. Tạo thành một tam giác đều;

B. Tạo thành một tam giác cân;

C. Tạo thành một tam giác;

D. Đồng quy tại trung điểm mỗi đường.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Viên chức

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Bright

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý