10 Bài tập Bài toán thực tiễn liên quan đến phương trình lượng giác (có lời giải)
46 người thi tuần này 4.6 318 lượt thi 10 câu hỏi 45 phút
🔥 Đề thi HOT:
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
10 Bài tập Bài toán thực tiễn liên quan đến giá trị lượng giác của góc lượng giác (có lời giải)
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
184 câu Trắc nghiệm Toán 11 Bài 1: Hàm số lượng giác có đáp án (Mới nhất)
10 Bài tập Rút gọn biểu thức và chứng minh đẳng thức lượng giác (có lời giải)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A
Giả sử thành phố A có đúng 15 giờ có ánh sáng mặt trời vào ngày thứ t0.
Ta có:
Mà d(t0) = 15 nên ta có:
⇔
⇔
⇔, k ∈ ℤ
⇔ t0 – 80 = 91 + 364k, k ∈ ℤ
⇔ t0 = 364k + 171, k ∈ ℤ
Mà 0 ≤ t0 ≤ 365
⇔ –171 ≤ 364k ≤ 194
⇔ –0,47 ≤ k ≤ 0,53
Mà k ∈ ℤ nên k = 0
Nếu k = 0 thì t0 = 171
Vậy thành phố A có đúng 15 giờ có ánh sáng mặt trời vào ngày thứ 171.
Lời giải
Hướng dẫn giải:
Đáp án đúng là: C
Giả sử thành phố A có đúng 9 giờ có ánh sáng mặt trời vào ngày thứ t0.
Ta có:
Mà d(t0) = 9 nên ta có:
⇔
⇔
⇔ , k ∈ ℤ
⇔ t0 – 80 = –91 + 364k , k ∈ ℤ
⇔ t0 = 364k – 11, k ∈ ℤ
Mà 0 ≤ t0 ≤ 365
⇔ 11 ≤ 364k ≤ 376
⇔ 0,03 ≤ k ≤ 1,03
Mà k ∈ ℤ nên k = 1
Nếu k = 1 thì t0 = 353
Vậy thành phố A có đúng 9 giờ có ánh sáng mặt trời vào ngày thứ 353.
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Vì v0 = 500 m/s và g = 9,8 m/s2 nên ta có phương trình quỹ đạo của quả đạn là:
\.
Quả đạn chạm đất khi y = 0, khi đó
⇔
⇔
⇔
⇔
Loại x = 0 (đạn pháo chưa được bắn)
Vậy tầm xa mà quả đạn đạt tới là (m).
Để quả đạn trúng mục tiêu cách vị trí đặt khẩu pháp 22 000 m thì x = 22 000 m.
Khi đó:
⇔ 
⇔ .
.
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
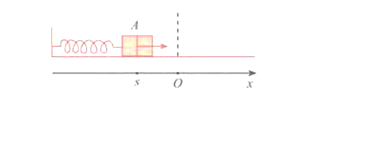
Khi s cm thì:
⇔
⇔
⇔ , k ∈ ℤ
⇔ , k ∈ ℤ
⇔, k ∈ ℤ
Khi k = 0 thì t = hoặc t = .
Lời giải
Hướng dẫn giải:
Đáp án đúng là: C
Khi góc tới là 45° thì góc khúc xạ bằng 30° nên ta có:
Tỉ số =
Khi góc tới là 60° thì ta có:
⇔
⇔
⇔
⇔
⇔.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.