4 bài tập Chủ đề 4. Động lượng có lời giải
64 người thi tuần này 4.6 755 lượt thi 4 câu hỏi 50 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Chuyên Phan Bội Châu- Nghệ An - lần 1 có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Thuận Thành - Bắc Ninh - Lần 1 có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Marie Curie - TPHCM có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Mạc Đĩnh Chi - HCM có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lí Nguyễn Khuyến Lê Thánh Tông - TPHCM có đáp án
(2023) Đề thi thử Vật Lí THPT Nguyễn Khuyến có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Yên Lạc - Vĩnh Phúc - Lần 1 có đáp án
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
a) Động lượng của vận động viên khi bắt đầu thả rơi là: \[{p_1} = m.{v_1} = 60.0 = 0kg.m/s\]
Vận tốc rơi tự do của vận động viên khi chạm mặt nước là: \[v = \sqrt {2gh} = \sqrt {2.10.4,5} = 3\sqrt {10} m/s\]
Động lượng của vận động viên khi chạm mặt nước là: \[{p_2} = m.{v_2} = 60.3\sqrt {10} = 180\sqrt {10} kg.m/s\]
b) Lực cản mà nước tác dụng lên người vận động viên là: \[{F_c} = \frac{{\Delta p}}{{\Delta t}} = \frac{{0 - 180\sqrt {10} }}{{0,5}} \approx - 1138,42N\]
Lời giải
Động lượng của hai vật lần lượt có độ lớn:
\[{p_1} = {m_1}.{v_1} = 0,4kg.m/s\]; \[{p_2} = {m_2}.{v_2} = 0,3kg.m/s\]; Động lượng của hệ: \[\overrightarrow p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} \]
a. Hình vẽ
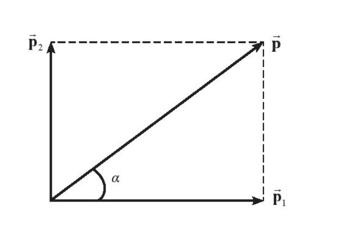
\[p = \sqrt {p_1^2 + p_2^2} = 0,5kg.m/s\]
\[\tan \alpha = \frac{{{p_2}}}{{{p_1}}} \Rightarrow \alpha \approx 37^\circ \]
(\[\overrightarrow p \] hợp với \[\overrightarrow {{p_1}} \] một góc 370)
b. Hình vẽ
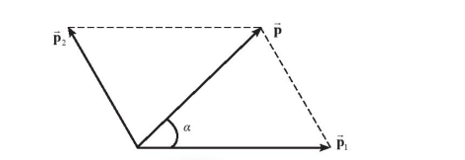
\[p = \sqrt {p_1^2 + p_2^2 + 2{p_1}{p_2}.\cos \theta } \approx 0,36kg.m/s\]
\[\cos \alpha = \frac{{{p^2} + p_1^2 - p_2^2}}{{2p.{p_1}}} = 0,7\]\[ \Rightarrow \alpha = 46^\circ \](\[\overrightarrow p \] hợp với \[\overrightarrow {{p_1}} \] một góc 460)
Lời giải
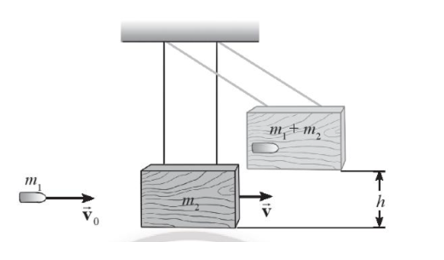
a. Chọn gốc thế năng tại vị trí thấp nhất của con lắc
Áp dụng định luật bảo toàn cơ năng cho hệ ngay sau khi va chạm cho đến khi con lắc đạt độ cao cực đại: \[\frac{1}{2}\left( {{m_1} + {m_2}} \right).{v^2} = \left( {{m_1} + {m_2}} \right).g.h\]\[ \Rightarrow v = \sqrt {2g.h} = \sqrt {2.9,8.0,05} \approx 0,99m/s\]
b. Áp dụng định luật bảo toàn động lượng cho hệ khối gỗ - viên đạn ngay trước và sau va chạm: \[{m_1}.\overrightarrow {{v_0}} = \left( {{m_1} + {m_2}} \right).\overrightarrow v \]\[ \Rightarrow \overrightarrow {{v_0}} = \frac{{\left( {{m_1} + {m_2}} \right).\overrightarrow v }}{{{m_1}}}\]
Ta có độ lớn: \[{v_0} = \frac{{\left( {{m_1} + {m_2}} \right).v}}{{{m_1}}} \approx 198,99m/s\]
Lời giải
Chọn chiều chuyển động ban đầu của xe cát là chiều dương, hệ vật gồm xe cát và đạn chuyển động theo phương ngang.
a. Đổi: \[{v_2} = 36km/h = 10m/s\]
Va chạm giữa viên đạn và toa xe là va chạm mềm nên động lượng của hệ (đạn + xe) là không đổi: \[{m_1}\overrightarrow {{v_1}} + {m_2}\overrightarrow {{v_2}} = \left( {{m_1} + {m_2}} \right)\overrightarrow v \]
Do \[\overrightarrow {{v_1}} \uparrow \uparrow \overrightarrow {{v_2}} \]\[ \Rightarrow v = \frac{{{m_1}{v_1} + {m_1}{v_2}}}{{{m_1} + {m_2}}} = \frac{{10.500 + 1000.10}}{{10 + 1000}} \approx 14,85m/s\]
b. Khi đạn bay đến ngược chiều xe cát (\[\overrightarrow {{v_1}} \uparrow \downarrow \overrightarrow {{v_2}} \]) thì ta có:
\[v = \frac{{{m_1}{v_1} + {m_1}{v_2}}}{{{m_1} + {m_2}}} = \frac{{10.\left( { - 500} \right) + 1000.10}}{{10 + 1000}} \approx 4,95m/s\]