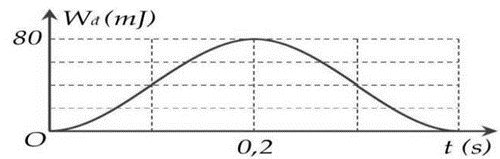
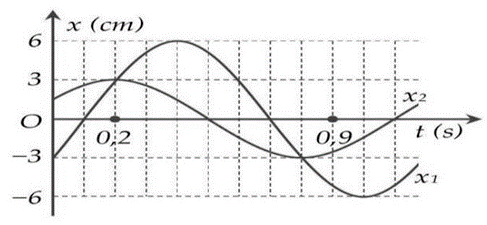
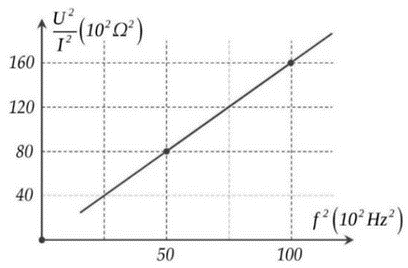
(2023) Đề thi thử Vật Lí Sở Bình Dương có đáp án
28 người thi tuần này 5.0 6.1 K lượt thi 40 câu hỏi 50 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Hòa Bình có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Lê Quý Đôn (Hải Phòng) có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Yên Bái có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Thái Bình có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Lai Châu có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Bình Thuận có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lý Cụm liên trường Ninh Bình có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lý Sở Thanh Hóa có đáp án
Danh sách câu hỏi:
Câu 1
D. \({s_0} = \frac{{{\alpha _0}}}{\ell }\)
Lời giải
Chọn B
Câu 2
D. \(\frac{R}{{\sqrt {{R^2} + {L^2}{\omega ^2}} }}\)
Lời giải
\({\bf{cos}}\varphi = \frac{R}{Z} = \frac{R}{{\sqrt {{R^2} + Z_L^2} }} \cdot \) Chọn D
Câu 3
D. \(\left| {f - {f_0}} \right|\)
Lời giải
Chọn A
Câu 4
B. \(k\lambda \) với \(k = 0; \pm 1; \pm 2; \ldots \)
Lời giải
Chọn B
Câu 5
D. \(\lambda \)
Lời giải
Chọn A
Câu 6
B. \(u = A{\rm{cos}}\left( {\omega t + \frac{{2\pi d}}{\lambda }} \right)\)
D. \(u = A{\rm{cos}}\left( {\omega t - \frac{{2\pi d}}{\lambda }} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
B. chu kì của dao động
D. lực kéo về của dao động
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
D. ampe (A)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
B. \(\pi \)
D. 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
D. \(W = \frac{1}{2}kA\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
D. \(\frac{{{I_0}}}{2}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
B. \(I = \frac{{U\sqrt 2 }}{{\sqrt {{R^2} + {{\left( {\omega L - \frac{1}{{\omega C}}} \right)}^2}} }}\)
D. \(I = \frac{U}{{\sqrt {{R^2} + {{\left( {\omega L + \frac{1}{{\omega C}}} \right)}^2}} }}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
D. \(x\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
B. \(\left( {2k + 1} \right)\frac{\pi }{4}\) với \(k = 0; \pm 1; \pm 2; \ldots \)
D. \(k\frac{\pi }{2}\) với \(k = 0; \pm 1; \pm 2; \ldots \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
D. \(\frac{{{U_0}}}{{R\sqrt 2 }}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. điểm \(M\) cách \(A\) một đoạn \(0,5\lambda \) là điểm bụng
B. điểm \(Q\) cách \(A\) một đoạn 3,5 3 là điểm nút
C. điểm \(N\) cách \(A\) một đoạn \(2\lambda \) là điểm bụng
D. điểm \(P\) cách \(A\) một đoạn \(2,25\lambda \) là điểm nút
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. biên độ dao động cưỡng bức không phụ thuộc vào biên độ ngoại lực cưỡng bức
B. biên độ dao động cương bức phụ thuộc vào pha ban đầu của lực cưỡng bức
C. biên độ dao động cưỡng bức phụ thuộc vào tần số dao động cưỡng bức
D. biên độ dao động cưỡng bức bằng biên độ lực cưỡng bức
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A. tốc độ truyền sóng là tốc độ dao động của các phần tử môi trường khi có sóng truyền qua
B. sóng ngang là sóng có phương dao động của các phần tử môi trường vuông góc với phương truyền sóng
C. bước sóng là quãng đường sóng truyền được trong 1 chu kì
D. khi sóng cơ truyền từ môi trường này sang môi trường khác, tần số của nó không đổi
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A. điện áp hiệu dụng hai đầu cuộn cảm lớn hơn điện áp hiệu dụng hai đầu tụ điện
B. điện áp hiệu dụng hai đầu điện trở có giá trị \(\frac{{{U_0}}}{{\sqrt 2 }}\)
C. hệ số công suất mạch bằng 0,5
D. điện áp hai đầu mạch sớm pha hơn cường độ dòng điện qua mạch
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. Khi vật đi từ vị trí cân bằng ra biên, tốc độ của vật tăng
B. Khi vật đi từ vị trí cân bằng ra biên, độ lớn gia tốc của vật giảm
C. Khi vật đi từ vị trí cân bằng ra biên, tốc độ của vật giảm
D. Khi vật đi từ biên về vị trí cân bằng, độ lớn gia tốc của vật tăng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
A. Sóng âm có tần số nhỏ hơn \(16{\rm{\;Hz}}\) gọi là hạ âm
B. Sóng âm có tần số lớn hơn \(20{\rm{kHz}}\) gọi là siêu âm
C. Khi truyền từ không khí vào chất lỏng bước sóng của sóng âm giảm
D. Sóng âm không được truyền trong chân không
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
D. \(220{\rm{\;W}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
B. \(18000{\rm{\;J}}\)
D. \(27000{\rm{\;J}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
D. \(5{\rm{\;cm}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
D. \(6,4{\rm{\;cm}}/{{\rm{s}}^2}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
D. \(64\mu {\rm{F}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
D. \(1,8{\rm{\;s}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
D. \(2{\rm{\;m}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
D. \(80{\rm{\;dB}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
D. \(19,4{\rm{\;N}}/{\rm{m}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
D. \(8,0{\rm{\;cm}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
D. \({l_1}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 37
D. \(200{\rm{\;V}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 38
D. \(109{\rm{\;cm}}/{\rm{s}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 40
A. \(0,04{\rm{H}}\)
B. \(0,51{\rm{H}}\)
D. \(0,2{\rm{H}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.