Bộ 5 đề thi giữa kì 2 Toán 9 Chân trời sáng tạo có đáp án - Đề 02
58 người thi tuần này 4.6 2.1 K lượt thi 22 câu hỏi 90 phút
🔥 Đề thi HOT:
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
123 bài tập Nón trụ cầu và hình khối có lời giải
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Hàm số 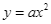 có đồ thị nằm bên trên trục hoành khi
có đồ thị nằm bên trên trục hoành khi
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Lời giải
Đáp án đúng là: D
Đồ thị hàm số ![]() có đồ thị nằm bên trên trục hoành khi
có đồ thị nằm bên trên trục hoành khi ![]()
Lời giải
Đáp án đúng là: D
Hàm số ![]() hay
hay ![]() có hệ số
có hệ số ![]() nên đồ thị hàm số nằm phía dưới trục hoành, nhận trục
nên đồ thị hàm số nằm phía dưới trục hoành, nhận trục ![]() làm trục đối xứng, có điểm cao nhất là gốc tọa độ.
làm trục đối xứng, có điểm cao nhất là gốc tọa độ.
Thay ![]() vào hàm số, ta được:
vào hàm số, ta được: 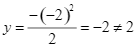 nên đồ thị hàm số không đi qua điểm
nên đồ thị hàm số không đi qua điểm ![]()
Vậy ta chọn phương án D.
Lời giải
Đáp án đúng là: C
Hai điểm ![]() và
và ![]() đối xứng với nhau qua trục tung
đối xứng với nhau qua trục tung ![]()
Lời giải
Đáp án đúng là: B
Ta viết phương trình ![]() về phương trình bậc hai một ẩn có hệ số
về phương trình bậc hai một ẩn có hệ số ![]() như sau:
như sau:
![]() .
.
Phương trình trên có hệ số ![]()
Lời giải
Đáp án đúng là: B
Ta có:  , suy ra phương trình có hai nghiệm phân biệt.
, suy ra phương trình có hai nghiệm phân biệt.
Lời giải
Đáp án đúng là: B
Nếu hai số ![]() có tổng là
có tổng là ![]() và tích là
và tích là ![]() thì hai số
thì hai số ![]() là nghiệm của phương trình
là nghiệm của phương trình ![]()
Lời giải
Đáp án đúng là: C
Phương trình ![]() có
có 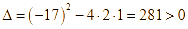 nên có hai nghiệm phân biệt
nên có hai nghiệm phân biệt ![]()
Theo định lí Viète, ta có: ![]()
Lời giải
Đáp án đúng là: B
Tâm đường tròn nội tiếp của một tam giác đều là giao điểm của ba đường phân giác, cũng đồng thời là giao điểm của ba đường trung trực, ba đường trung tuyến, ba đường cao.
Lời giải
Đáp án đúng là: C
Tam giác vuông có cạnh huyền ![]() cm thì có bán kính đường tròn ngoại tiếp là
cm thì có bán kính đường tròn ngoại tiếp là ![]()
Lời giải
Đáp án đúng là: B
Tứ giác ![]() có tất cả các đỉnh đều nằm trên một đường tròn nên là tứ giác nội tiếp.
có tất cả các đỉnh đều nằm trên một đường tròn nên là tứ giác nội tiếp.
Câu 11
Cho tam giác đều , các đường cao
, các đường cao 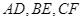 cắt nhau tại
cắt nhau tại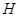 . Gọi
. Gọi 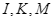 theo thứ tự là trung điểm của
theo thứ tự là trung điểm của 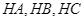 . Đa giác
. Đa giác 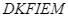 là hình gì?
là hình gì?
Lời giải
Đáp án đúng là: D
Đa giác ![]() có 6 cạnh nên là lục giác đều.
có 6 cạnh nên là lục giác đều.
Lời giải
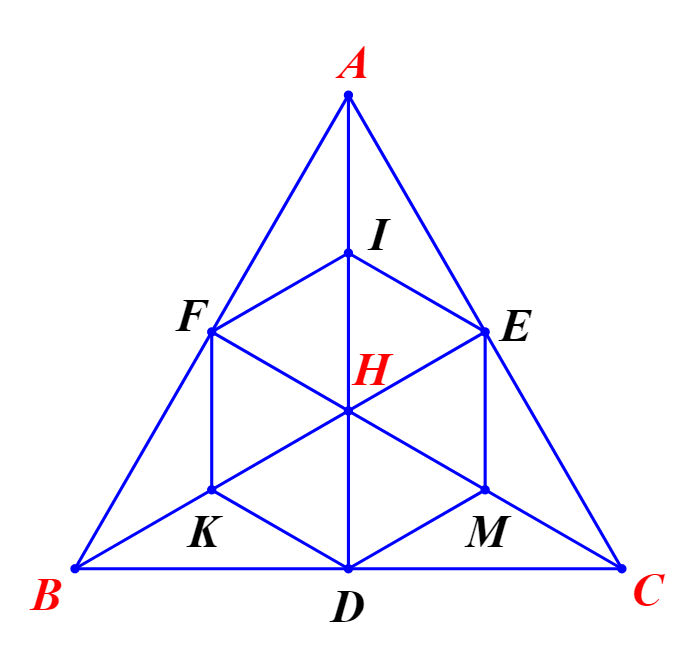
Đáp án đúng là: C
Ta có ![]() là tâm hình vuông
là tâm hình vuông ![]() nên
nên ![]() là trung điểm của
là trung điểm của ![]() do đó
do đó ![]() và
và ![]()
Như vậy, phép quay ngược chiều ![]() tâm
tâm ![]() biến điểm
biến điểm ![]() thành điểm
thành điểm ![]()
Câu 13
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Cho hàm số 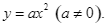
a) Nếu  hàm số luôn có giá trị âm với mọi giá trị âm của biến.
hàm số luôn có giá trị âm với mọi giá trị âm của biến.
b) Nếu đồ thị hàm số đi qua điểm 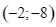 thì
thì 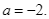
c) Khi 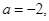 đồ thị hàm số nằm trên trục hoành.
đồ thị hàm số nằm trên trục hoành.
d) Khi 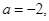 đồ thị hàm số cắt đường thẳng
đồ thị hàm số cắt đường thẳng 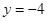 tại hai điểm phân biệt.
tại hai điểm phân biệt.
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Cho hàm số ![]()
a) Nếu ![]() hàm số luôn có giá trị âm với mọi giá trị âm của biến.
hàm số luôn có giá trị âm với mọi giá trị âm của biến.
b) Nếu đồ thị hàm số đi qua điểm ![]() thì
thì ![]()
c) Khi ![]() đồ thị hàm số nằm trên trục hoành.
đồ thị hàm số nằm trên trục hoành.
d) Khi ![]() đồ thị hàm số cắt đường thẳng
đồ thị hàm số cắt đường thẳng ![]() tại hai điểm phân biệt.
tại hai điểm phân biệt.
Lời giải
a) Đúng. b) Đúng. c) Sai. d) Đúng.
Xét hàm số ![]()
⦁ Với mọi ![]() ta có
ta có ![]() .
.
Nếu ![]() thì
thì ![]() nên hàm số luôn có giá trị âm với mọi giá trị âm của biến. Do đó ý a) là đúng.
nên hàm số luôn có giá trị âm với mọi giá trị âm của biến. Do đó ý a) là đúng.
⦁ Thay ![]() vào hàm số, ta được:
vào hàm số, ta được: ![]() hay
hay ![]() suy ra
suy ra ![]() Do đó ý b) là đúng.
Do đó ý b) là đúng.
⦁ Khi ![]() thì đồ thị hàm số
thì đồ thị hàm số ![]() luôn nằm phía dưới trục hoành. Do đó ý c) là sai.
luôn nằm phía dưới trục hoành. Do đó ý c) là sai.
⦁ Khi ![]() đồ thị hàm số
đồ thị hàm số ![]() luôn nằm phía dưới trục hoành nên cắt đường thẳng
luôn nằm phía dưới trục hoành nên cắt đường thẳng ![]() tại hai điểm phân biệt. Do đó ý d) là đúng.
tại hai điểm phân biệt. Do đó ý d) là đúng.
Câu 14
Cho bốn điểm 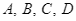 đều nằm trên đường tròn tâm
đều nằm trên đường tròn tâm 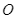 đường kính
đường kính 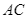 và
và 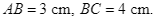
a) Tứ giác 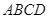 nội tiếp đường tròn
nội tiếp đường tròn 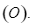
b) 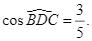
c) Đường tròn tâm 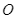 ngoại tiếp tam giác
ngoại tiếp tam giác 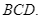
d) Bán kính đường tròn ngoại tiếp tam giác 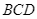 bằng
bằng 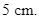
Cho bốn điểm ![]() đều nằm trên đường tròn tâm
đều nằm trên đường tròn tâm ![]() đường kính
đường kính ![]() và
và ![]()
a) Tứ giác ![]() nội tiếp đường tròn
nội tiếp đường tròn ![]()
b) ![]()
c) Đường tròn tâm ![]() ngoại tiếp tam giác
ngoại tiếp tam giác ![]()
d) Bán kính đường tròn ngoại tiếp tam giác ![]() bằng
bằng ![]()
Lời giải
a) Đúng. b) Đúng. c) Đúng. d) Sai.
|
⦁ Vì bốn điểm ⦁ Tứ giác Xét đường tròn tâm |
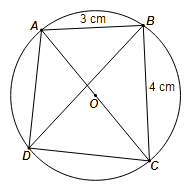 |
Xét ![]() vuông tại
vuông tại ![]() theo định lí Pythagore ta có
theo định lí Pythagore ta có ![]() , suy ra
, suy ra ![]()
Do đó ![]() Như vậy, ý b) là đúng.
Như vậy, ý b) là đúng.
⦁ Tứ giác ![]() nội tiếp đường tròn
nội tiếp đường tròn ![]() nên đường tròn
nên đường tròn ![]() đi qua các điểm
đi qua các điểm ![]()
Như vậy, đường tròn tâm ![]() ngoại tiếp tam giác
ngoại tiếp tam giác ![]() Do đó ý c) là đúng.
Do đó ý c) là đúng.
⦁ Đường tròn tâm ![]() có đường kính là
có đường kính là ![]() nên bán kính đường tròn ngoại tiếp tam giác
nên bán kính đường tròn ngoại tiếp tam giác ![]() bằng
bằng ![]() Do đó ý d) là sai.
Do đó ý d) là sai.
Câu 15
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Tìm giá trị nguyên lớn nhất của 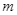 để phương trình
để phương trình 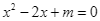 có nghiệm.
có nghiệm.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Lời giải
Đáp số: 1.
Phương trình ![]() có
có ![]()
Phương trình ![]() có nghiệm khi
có nghiệm khi ![]() hay
hay ![]() suy ra
suy ra ![]()
Như vậy, giá trị nguyên lớn nhất của ![]() thỏa mãn yêu cầu đề bài là
thỏa mãn yêu cầu đề bài là ![]()
Câu 16
Với giá trị nào của 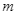 để parabol
để parabol 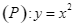 và đường thẳng
và đường thẳng 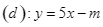 cắt nhau tại hai điểm phân biệt có hoành độ
cắt nhau tại hai điểm phân biệt có hoành độ 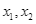 là số nguyên tố?
là số nguyên tố?
Lời giải
Đáp số: 6.
Phương trình hoành độ giao điểm của ![]() và
và ![]() có dạng
có dạng ![]() (1)
(1)
Ta có: ![]()
Để parabol ![]() cắt đường thẳng
cắt đường thẳng ![]() tại hai điểm phân biệt thì phương trình hoành độ giao điểm luôn có hai nghiệm phân biệt, tức là
tại hai điểm phân biệt thì phương trình hoành độ giao điểm luôn có hai nghiệm phân biệt, tức là ![]() hay 25 - 4m > 0 nên
hay 25 - 4m > 0 nên ![]()
Theo định lí Viète ta có 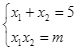
Vì ![]() có giá trị là số nguyên tố nên
có giá trị là số nguyên tố nên ![]() suy ra
suy ra ![]()
Vậy ![]() là giá trị cần tìm.
là giá trị cần tìm.
Câu 17
Cho tứ giác 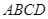 nội tiếp đường tròn (hình vẽ) có hai cạnh
nội tiếp đường tròn (hình vẽ) có hai cạnh 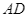 và
và 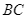 cắt nhau tại
cắt nhau tại 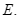 Hãy tính số đo độ của góc
Hãy tính số đo độ của góc 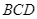 khi biết
khi biết 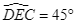 và
và 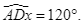
Lời giải

Đáp số: 75.
Ta có ![]() (hai góc kề bù)
(hai góc kề bù)
Tứ giác ![]() nội tiếp đường tròn nên
nội tiếp đường tròn nên ![]() (tổng hai góc đối nhau trong một tứ giác nội tiếp).
(tổng hai góc đối nhau trong một tứ giác nội tiếp).
Suy ra ![]()
Mà ![]() là góc ngoài tại đỉnh
là góc ngoài tại đỉnh ![]() của tam giác
của tam giác ![]() nên
nên ![]()
Suy ra ![]()
Lại có ![]() (hai góc kề bù) và
(hai góc kề bù) và ![]() (tổng hai góc đối nhau trong tứ giác
(tổng hai góc đối nhau trong tứ giác ![]() nội tiếp).
nội tiếp).
Suy ra ![]()
Câu 18
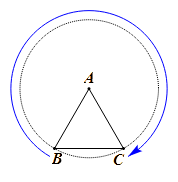
Cho tam giác đều 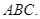 Góc quay của phép quay thuận chiều kim đồng hồ với tâm
Góc quay của phép quay thuận chiều kim đồng hồ với tâm 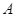 biến điểm
biến điểm 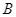 thành điểm
thành điểm 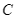 là bao nhiêu độ?
là bao nhiêu độ?
Lời giải
Đáp số: 300.
|
Xét Phép quay thuận chiều kim đồng hồ với tâm
Vậy góc quay của phép quay đó là |
 |
Câu 19
B. TỰ LUẬN (3,0 điểm)
Giải bài toán sau bằng cách lập phương trình:
Bạn An chia đoạn thẳng 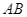 dài 10 cm thành hai đoạn sao cho tỉ số giữa đoạn lớn với đoạn
dài 10 cm thành hai đoạn sao cho tỉ số giữa đoạn lớn với đoạn 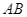 bằng tỉ số giữa đoạn nhỏ với đoạn lớn. Hãy tìm tỉ số ấy.
bằng tỉ số giữa đoạn nhỏ với đoạn lớn. Hãy tìm tỉ số ấy.
B. TỰ LUẬN (3,0 điểm)
Bạn An chia đoạn thẳng ![]() dài 10 cm thành hai đoạn sao cho tỉ số giữa đoạn lớn với đoạn
dài 10 cm thành hai đoạn sao cho tỉ số giữa đoạn lớn với đoạn ![]() bằng tỉ số giữa đoạn nhỏ với đoạn lớn. Hãy tìm tỉ số ấy.
bằng tỉ số giữa đoạn nhỏ với đoạn lớn. Hãy tìm tỉ số ấy.
Lời giải
Giả sử điểm ![]() chia đoạn thẳng
chia đoạn thẳng ![]() thành hai đoạn thẳng thỏa mãn điều kiện bài toán,
thành hai đoạn thẳng thỏa mãn điều kiện bài toán, ![]()
Gọi độ dài của ![]() (0 < x < 10) suy ra
(0 < x < 10) suy ra ![]()
Theo đề bài, bạn An chia đoạn thẳng ![]() thành hai đoạn sao cho tỉ số giữa đoạn lớn với đoạn
thành hai đoạn sao cho tỉ số giữa đoạn lớn với đoạn ![]() bằng tỉ số giữa đoạn nhỏ với đoạn lớn nên ta có
bằng tỉ số giữa đoạn nhỏ với đoạn lớn nên ta có ![]() hay
hay ![]() .
.
Giải phương trình:
![]()
![]()
![]()
![]()
Giải phương trình trên ta được ![]()
![]()
Ta thấy chỉ có giá trị ![]() thỏa mãn điều kiện.
thỏa mãn điều kiện.
Vậy ![]() tỉ số cần tìm là
tỉ số cần tìm là ![]()
Lời giải
Xét phương trình ![]() có
có ![]()
Với mọi ![]() ta thấy
ta thấy ![]() nên
nên ![]()
Do đó, phương trình đã cho có hai nghiệm phân biệt ![]() với mọi giá trị của
với mọi giá trị của ![]()
Theo định lí Viète, ta có: ![]()
Ta có: ![]()
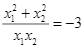
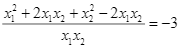
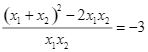
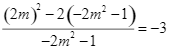
![]()
![]()
![]()
![]() (thỏa mãn) hoặc
(thỏa mãn) hoặc ![]() (thỏa mãn).
(thỏa mãn).
Vậy 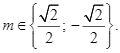
Câu 21
Cho đường tròn tâm 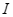 nội tiếp tam giác
nội tiếp tam giác 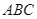 tiếp xúc với
tiếp xúc với 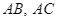 lần lượt tại
lần lượt tại 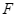 và
và 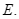 Kẻ
Kẻ 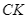 vuông góc với
vuông góc với 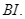 Chứng minh rằng:
Chứng minh rằng:
Tứ giác 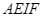 là tứ giác nội tiếp.
là tứ giác nội tiếp.
Cho đường tròn tâm ![]() nội tiếp tam giác
nội tiếp tam giác ![]() tiếp xúc với
tiếp xúc với ![]() lần lượt tại
lần lượt tại ![]() và
và ![]() Kẻ
Kẻ ![]() vuông góc với
vuông góc với ![]() Chứng minh rằng:
Chứng minh rằng:
Tứ giác ![]() là tứ giác nội tiếp.
là tứ giác nội tiếp.
Lời giải
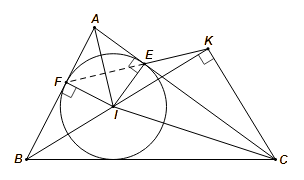
Vì ![]() là tiếp điểm của đường tròn
là tiếp điểm của đường tròn ![]() nội tiếp tam giác
nội tiếp tam giác ![]() nên
nên ![]()
Do đó ![]() , nên hai tam giác
, nên hai tam giác ![]() là hai tam giác vuông có cùng cạnh huyền
là hai tam giác vuông có cùng cạnh huyền ![]()
Do đó đường tròn ngoại tiếp hai tam giác ![]() là đường tròn đường kính
là đường tròn đường kính ![]() hay bốn điểm
hay bốn điểm ![]() cùng nằm trên đường tròn đường kính
cùng nằm trên đường tròn đường kính ![]()
Vậy tứ giác ![]() là tứ giác nội tiếp.
là tứ giác nội tiếp.
Câu 22
Cho đường tròn tâm  nội tiếp tam giác
nội tiếp tam giác 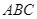 tiếp xúc với
tiếp xúc với 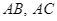 lần lượt tại
lần lượt tại 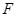 và
và 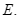 Kẻ
Kẻ 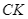 vuông góc với
vuông góc với 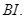 Chứng minh rằng:
Chứng minh rằng:
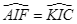 và ba điểm
và ba điểm 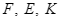 thẳng hàng.
thẳng hàng.
Lời giải
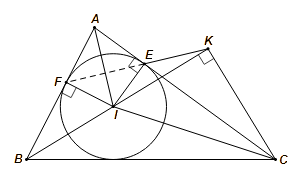
Đường tròn tâm ![]() nội tiếp tam giác
nội tiếp tam giác ![]() nên
nên ![]() là các đường phân giác của tam giác.
là các đường phân giác của tam giác.
Do đó ![]() .
.
Ta có: ![]() . (1)
. (1)
![]() (2)
(2)
Xét ![]() có
có ![]() là góc ngoài tại đỉnh
là góc ngoài tại đỉnh ![]() nên
nên ![]() (3)
(3)
Từ (1), (2) và (3) suy ra ![]() (4)
(4)
Tứ giác ![]() là tứ giác nội tiếp nên
là tứ giác nội tiếp nên ![]() (hai góc nội tiếp cùng chắn cung
(hai góc nội tiếp cùng chắn cung ![]() (5)
(5)
Chứng minh tương tự câu 1, ta có tứ giác ![]() nội tiếp đường tròn đường kính
nội tiếp đường tròn đường kính ![]()
Do đó ![]() (hai góc nội tiếp cùng chắn cung
(hai góc nội tiếp cùng chắn cung ![]() (6)
(6)
Từ (4), (5), (6) ta có ![]() .
.
Mà ![]() nên
nên ![]() hay ba điểm
hay ba điểm ![]() thẳng hàng.
thẳng hàng.
412 Đánh giá
50%
40%
0%
0%
0%