12 bài tập Một số bài toán liên quan đến tính đơn điệu, cực trị có chứa tham số có đáp án
31 người thi tuần này 4.6 241 lượt thi 12 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề cương ôn tập cuối kì 2 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Chương IV. Nguyên hàm và tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Tự luận
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Phương trình mặt phẳng
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 4. Ứng dụng hình học của tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 3. Tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 2. Nguyên hàm của một số hàm số sơ cấp
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Nguyên hàm
Đề cương ôn tập giữa kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Tự luận
Danh sách câu hỏi:
Câu 1
A. 27;
B. 35;
C. 44;
D. 54.
Lời giải
Đáp án đúng là: C
y = x3 − 3x2 +3(m + 2)x + 3m – 2025
Hàm số đã cho xác định trên D = ℝ.
Để hàm số đồng biến trên ℝ y' = 3x2 – 6x + 3(m + 2) ≥ 0, ∀x ∈ ℝ
\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a > 0}\\{\Delta ' \le 0}\end{array}{\rm{ }} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{3 > 0{\rm{ }}}\\{9 - 9(m + 2) \le 0}\end{array} \Leftrightarrow m \ge - 1{\rm{ }}} \right.} \right.\].
Vậy m ≥ −1 thì hàm số đồng biến trên ℝ.
Do m ∈ [−10; 10), m ∈ ℤ nên tổng các giá trị nguyên của tham số là 44.
Câu 2
A. \(P = \frac{9}{4}\);
B. \(P = \frac{{13}}{2}\);
C. P = 4;
D. \(P = \frac{{13}}{4}\).
Lời giải
Đáp án đúng là: B
Hàm số đã cho xác định trên D = ℝ.
Để hàm số đồng biến trên ℝ y' = 3x2 – 2(2m – 1)x + (2 – m) ≥ 0, ∀x ∈ ℝ\[ \Leftrightarrow \left\{ \begin{array}{l}a = 3 > 0\\\Delta ' = {\left( {2m - 1} \right)^2} - 3\left( {2 - m} \right) = 4{m^2} - m - 5 \le 0\end{array} \right. \Leftrightarrow - 1 \le m \le \frac{5}{4}\].
Vậy \[ - 1 \le m \le \frac{5}{4}\] thì hàm số đồng biến trên ℝ.
Do \(m \in \left[ {a;\frac{b}{c}} \right]\) nên \(\left\{ \begin{array}{l}a = - 1\\b = 5\\c = 4\end{array} \right. \Rightarrow P = \frac{{{a^2} + {b^2}}}{c} = \frac{{13}}{2}\).
Câu 3
A. (−∞; 1];
B. (−∞; 4];
C. (−∞; 1);
D. (−∞; 4).
Lời giải
Đáp án đúng là: B
Ta có y' = 3x2 – 6x + 4 – m.
Yêu cầu bài toán y' ≥ 0, ∀x ∈ (2; +∞)
3x2 – 6x + 4 – m ≥ 0, ∀x ∈ (2; +∞)
m ≤ 3x2 – 6x + 4, ∀x ∈ (2; +∞)
m ≤ \(\mathop {\min }\limits_{\left( {2; + \infty } \right)} g\left( x \right)\) với g(x) = 3x2 – 6x + 4.
Ta có g'(x) = 6x – 6; g'(x) = 0 6x – 6 = 0 x = 1.
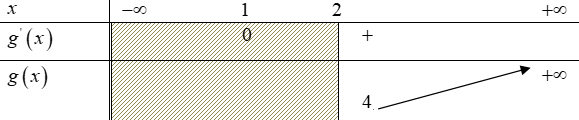
Dựa vào bảng biến thiên, suy ra: m ≤ 4 thỏa yêu cầu bài toán.
Vậy: m ∈ (−∞; 4] thì hàm số đồng biến trên khoảng (2; +∞).
Lời giải
Đáp án đúng là: C
Yêu cầu bài toán y' = −3x3 + 9x – 2m – 15 ≤ 0, ∀x ∈ (0; +∞) và dấu bằng xảy ra tại hữu hạn điểm thuộc (0; +∞) 3x3 − 9x + 15 ≥ – 2m, ∀x ∈ (0; +∞).
Xét hàm số g(x) = 3x3 − 9x + 15 trên (0; +∞).
Ta có: g'(x) = 9x2 – 9; g'(x) = 0 x = 1 hoặc x = −1 (loại).
Bảng biến thiên:
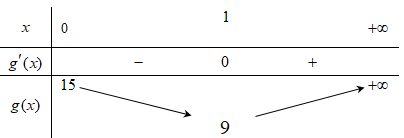
Từ bảng biến thiên ta có: \( - 2m \le 9 \Leftrightarrow m \ge - \frac{9}{2}\).
Vậy m ∈ {−4; −3; −2; −1}.
Lời giải
Đáp án đúng là: B
Tập xác định: D = ℝ\{−4}.
Ta có \(y' = \frac{{4 - {m^2}}}{{{{\left( {x + 4} \right)}^2}}}.\)
Hàm số đồng biến trên từng khoảng xác định khi và chỉ khi \(y' > 0\;\forall x \in D \Leftrightarrow \frac{{4 - {m^2}}}{{{{\left( {x + 4} \right)}^2}}} > 0\;\forall x \ne - 4 \Leftrightarrow - 2 < m < 2.\)
Vì m ∈ ℤ m ∈ {−1; 0; 1}.
Vậy có 3 giá trị m nguyên để bài toán thỏa mãn.
Câu 6
A. P = −4;
B. P = 4;
C. P = −3;
D. P = −5.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 2038;
B. 2020;
C. 2018;
D. 2021.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. 47;
B. 44;
C. 46;
D. 45.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. ab ≤ 0;
B. ab < 0;
C. ab > 0;
D. ab ≥ 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. m ∈ (−∞; 6) ∪ (0; +∞);
B. m ∈ (−6; 0);
C. m ∈ [−6; 0);
D. m ∈ [−6; 0].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.