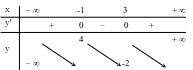Bài tập ôn tập Toán 12 Cánh diều Chương 1 có đáp án
33 người thi tuần này 4.6 271 lượt thi 55 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề cương ôn tập cuối kì 2 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Chương IV. Nguyên hàm và tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Tự luận
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Phương trình mặt phẳng
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 4. Ứng dụng hình học của tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 3. Tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 2. Nguyên hàm của một số hàm số sơ cấp
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Nguyên hàm
Đề cương ôn tập giữa kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Tự luận
Danh sách câu hỏi:
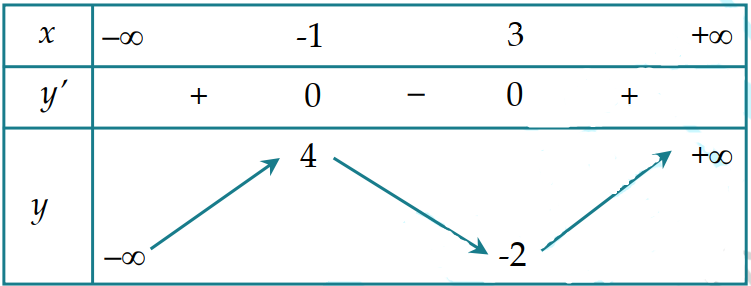
Câu 1
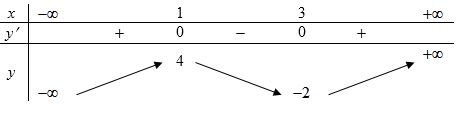
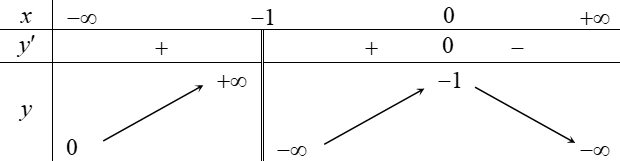
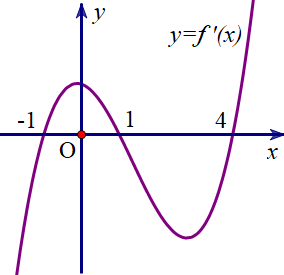
\(\left( {3; + \infty } \right)\).
\(\left( {1;3} \right)\).
\(\left( { - \infty ;4} \right)\).
\(\left( {0; + \infty } \right)\).
Lời giải
Chọn A
Căn cứ vào BBT ta thấy: Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {3; + \infty } \right)\).
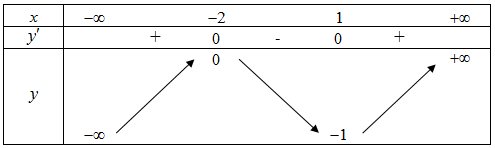
Câu 2
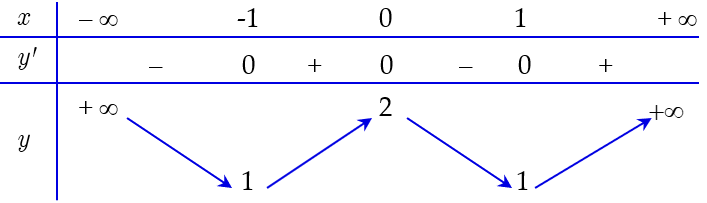
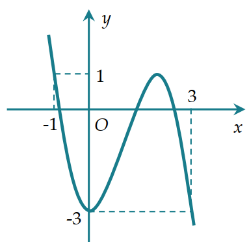
\[\left( {0\,;1} \right)\].
\[\left( { - 1;0} \right)\].
\[\left( {1; + \infty } \right)\].
\[\left( {0; + \infty } \right)\].
Lời giải
Chọn A
Hàm số đã cho nghịch biến trên khoảng \[\left( {0\,;1} \right)\].
Câu 3
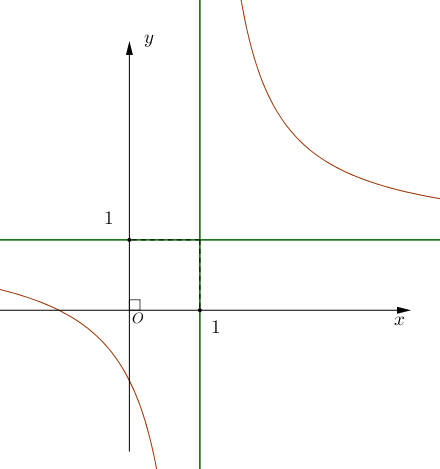
Hàm số nghịch biến trên các khoảng \[\left( { - \infty ;1} \right)\]và \[\left( {1; + \infty } \right)\].
Hàm số đồng biến trên các khoảng \[\left( { - \infty ;1} \right)\]\[ \cup \]\[\left( {1; + \infty } \right)\].
Hàm số đồng biến trên các khoảng \[\left( { - \infty ;1} \right)\]và \[\left( {1; + \infty } \right)\].
Hàm số nghịch biến trên các khoảng \[\left( { - \infty ; - 1} \right)\] và \[\left( { - 1; + \infty } \right)\].
Lời giải
Chọn A
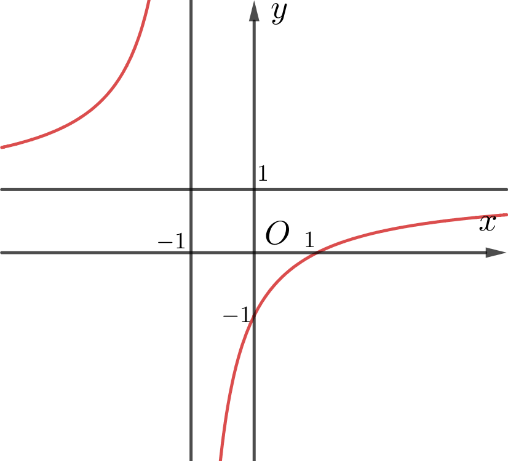
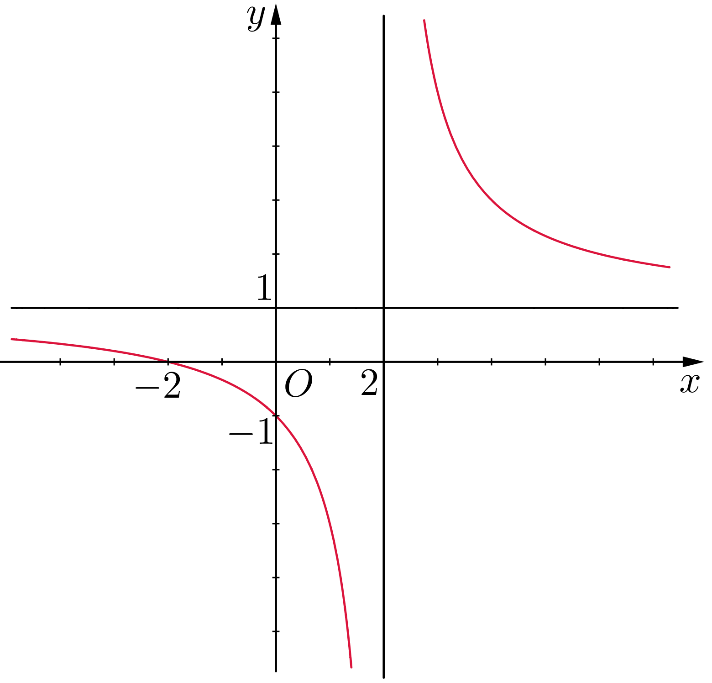
Ta có \[y = \frac{{x + 2}}{{x - 1}} \Rightarrow y' = \frac{{ - 3}}{{{{(x - 1)}^2}}} < 0,\forall x \ne 1\].
Do đó hàm số nghịch biến trên các khoảng \[\left( { - \infty ;1} \right)\]và \[\left( {1; + \infty } \right)\].
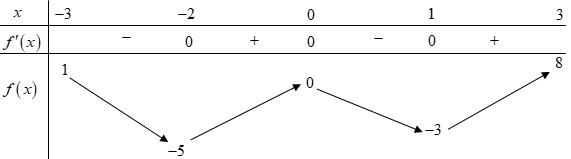
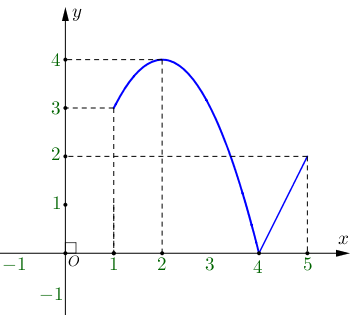
Câu 4
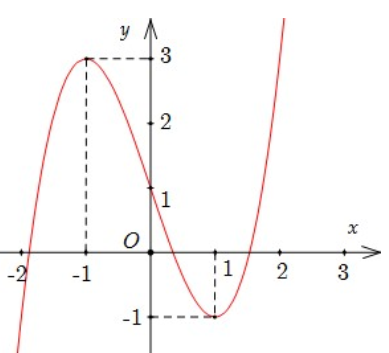
\[f\left( 0 \right) > f\left( 1 \right)\].
\[f\left( 2 \right) < f\left( 3 \right)\].
\[f\left( { - 1} \right) = f\left( 1 \right)\].
\[f\left( { - 1} \right) > f\left( 3 \right)\].
Lời giải
Chọn B
Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng \[\left( {1;3} \right)\] cho nên \[f\left( 2 \right) < f\left( 3 \right)\].
Câu 5
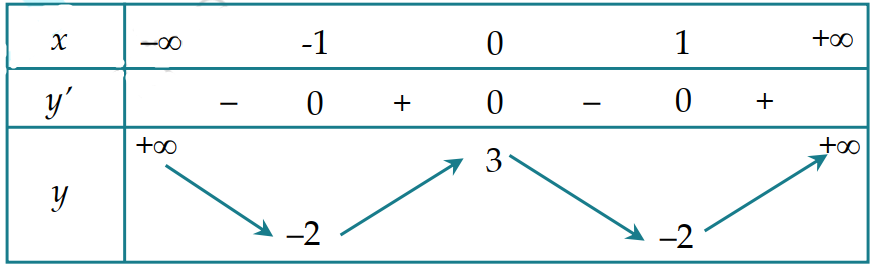
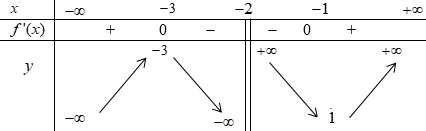
Cho hàm số \[f\left( x \right)\] có bảng biến thiên như sau:
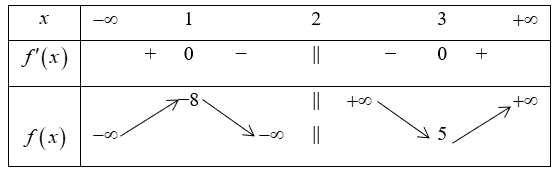
Giá trị cực tiểu của hàm số đã cho bằng
\[ - 8\].
\[5\].
\[3\].
\[1\].
Lời giải
Chọn B
Dựa vào bảng biến thiên của hàm số \[f\left( x \right)\].
Hàm số đạt cực tiểu tại \[x = 3 \Leftrightarrow f\left( x \right) = 5\].
Câu 6
\(6\).
\(3\).
\(1\).
\(2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
\(x = 3\).
\[x = - 2\].
\(x = 4\).
\(x = - 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
\[ - 1\].
\[4\].
\[ - 2\].
\[3\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
\(1\).
\( - 2\).
\(0\).
\( - 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Hàm số đồng biến trên \(\left( { - \infty ;1} \right)\) và nghịch biến trên \(\left( {1; + \infty } \right)\).
Hàm số nghịch biến trên \(\mathbb{R}\).
Hàm số nghịch biến trên \(\left( { - \infty ;1} \right)\) và đồng biến trên \(\left( {1; + \infty } \right)\).
Hàm số đồng biến trên \(\mathbb{R}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Hàm số đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ; + \infty } \right)\).
Hàm số đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
\(5\).
\(\frac{1}{3}\).
\( - \frac{1}{3}\).
\( - 5\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
\(1\).
\(0\).
\( - \frac{4}{3}\).
\(\frac{4}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
Đường thẳng \[x = 0\] và \[x = - 1\] là tiệm cận đứng của đồ thị hàm số.
Đồ thị hàm số không có tiệm cận đứng.
Đồ thị hàm số có duy nhất đường tiệm cận đứng là \[x = 0\].
Đồ thị hàm số có duy nhất đường tiệm cận đứng là \[x = - 1\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
\(y = 2\).
\(y = \frac{3}{4}\).
\(y = - 3\).
\(x = - 3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
\(\left( C \right)\) không có tiệm cận ngang.
\(\left( C \right)\) có hai tiệm cận đứng.
\(\left( C \right)\) không có tiệm cận đứng.
\(\left( C \right)\)có một tiệm cận ngang và một tiệm cận đứng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
\[y = 1\].
\[x = 1\].
\[x = \frac{1}{2}\].
\[y = \frac{1}{2}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
\(x = 2\).
\(x = 0\).
\(y = 1\).
\(x = 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
\(y = x\).
\(y = x - 1\).
\(y = 2x - 1\).
\(y = x + 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
\(y = \frac{{x - 1}}{{x + 1}}\).
\(y = \frac{{2x - 1}}{{x - 1}}\).
\(y = \frac{{x + 2}}{{x - 1}}\).
\(y = \frac{{3x - 1}}{{x + 1}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
\(y = - {x^3} + 3x - 1\).
\(y = {x^3} + 3x + 1\).
\(y = {x^3} - 3x + 1\).
\(y = - {x^3} - 3x + 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
\(\left( {0;1} \right)\).
\(\left( {1;0} \right)\).
\(\left( {0; - 1} \right)\).
\(\left( {1;1} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
\[y = {x^3} - 3x - 1\].
\[y = - {x^4} + 2{x^2} - 1\].
\[{x^4} - 2{x^2} - 1\].
\[y = - {x^3} + 3x - 1\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
\(y = \frac{{x + 2}}{{x - 2}}\).
\(y = - {x^3} + 3{x^2} - 1\).
\(y = \frac{{x - 1}}{{x - 2}}\).
\(y = {x^4} - 3{x^2} + 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.