5 câu Trắc nghiệm Toán 10 chân trời sáng tạo Ba đường conic trong mặt phẳng tọa độ (Vận dụng) có đáp án
19 người thi tuần này 4.6 2.1 K lượt thi 5 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
20 câu trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 7 (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 6. Ba đường conic (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 5. Phương trình đường trò (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 3. Phương trình đường thẳn (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 2. Biểu thức tọa độ của các phép toán vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 1. Tọa độ của vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài ôn tập cuối chương 6 (Đúng sai - trả lời ngắn) có đáp án
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
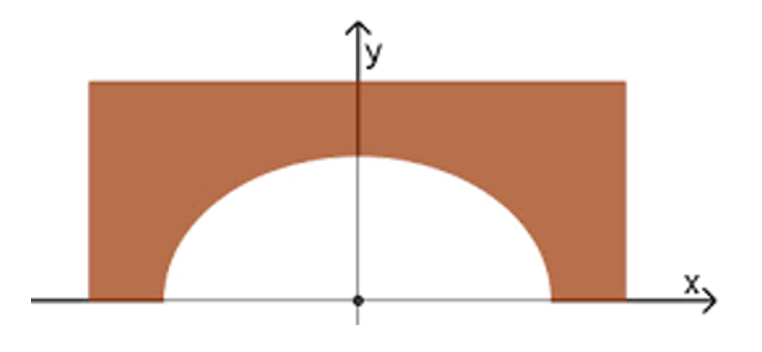
Ta thấy chiều cao của cổng hầm là: b = 10 – 4 = 6 (m).
Chiều rộng của cổng hầm là: 2a = 20 – 2.2 = 16 (m).
Suy ra a = 8 (m).
Khi đó ta có phương trình chính tắc của (E) là: .
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
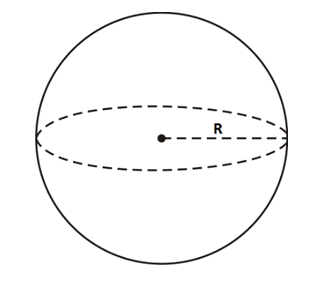
Ta thấy đường kính đường tròn chính bằng trục lớn của Elip.
Nên 2a = 2R = 20 (cm), suy ra a = 10 (cm).
Ta có tiêu cự của Elip là 16 cm nên 2c = 16, suy ra c = 8 (cm).
Khi đó b2 = c2 – a2 = 102 – 82 = 36
Phương trình chính tắc của Elip là: .
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
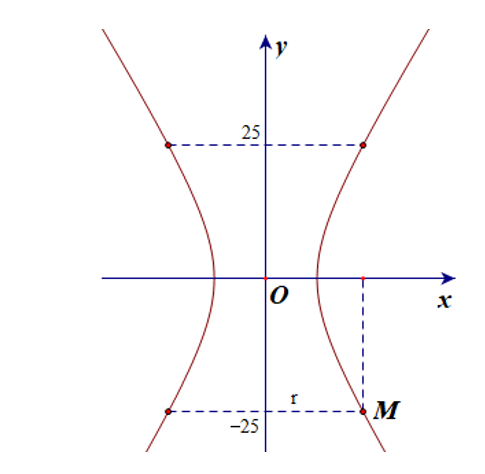
Gọi r là bán kính đáy của tháp (r > 0).
Do khoảng cách từ nóc tháp đến tâm đối xứng O của hypebol bằng khoảng cách từ tâm đối xứng O đến đáy tháp và do tính đối xứng của hypebol nên ta có hai bán kính của nóc và đáy tháp đều bằng nhau.
Chọn điểm M(r; –25) nằm trên hypebol.
Ta suy ra .
.
.
Suy ra (m).
Vậy bán kính đáy của tháp bằng khoảng 22,25 m.
Ta chọn phương án B.
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
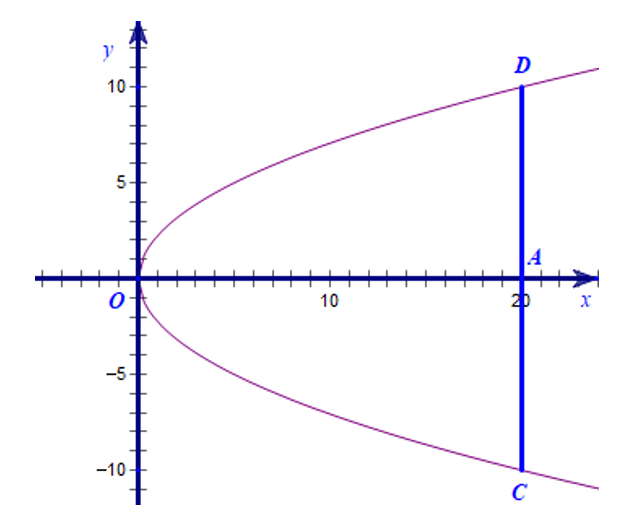
Chọn hệ trục tọa độ Oxy như hình vẽ.
Gọi O là đỉnh cổng, A là chân cổng và C, D lần lượt là hai bên trái, phải chân cổng.
Theo bài ra ta có: OA = 20 m, CD = 20 m.
Gọi phương trình Parabol của cổng là y2 =2px.
Ta có: AC = AD = CD : 2 = 10 (m)
Do đó điểm D có tung độ là 10.
OA = 20 nên điểm D có hoành độ là 20.
Thay D(20; 10) vào phương trình (P) ta có:
Suy ra y2 = 5x.
Thay tọa độ điểm E cách đỉnh 4 m (x = 4) vào (P) ta có:
y2 = 5x = 5 . 4 = 20
Vậy bề rộng của cổng tại chỗ cách đỉnh 4 m là m.
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
Tọa độ giao điểm của d và Elip là nghiệm của hệ phương trình:
Hai đồ thị có hai giao điểm phân biệt khi và chỉ khi (*) có hai nghiệm phân biệt y.
– 4m2 + 32 > 0
m2 < 8
Vậy ta chọn phương án D.