Bộ 5 đề thi giữa kì 1 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Đề 4
23 người thi tuần này 4.6 1 K lượt thi 21 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề cương ôn tập cuối kì 2 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Chương IV. Nguyên hàm và tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Tự luận
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Phương trình mặt phẳng
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 4. Ứng dụng hình học của tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 3. Tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 2. Nguyên hàm của một số hàm số sơ cấp
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Nguyên hàm
Đề cương ôn tập giữa kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Tự luận
Danh sách câu hỏi:
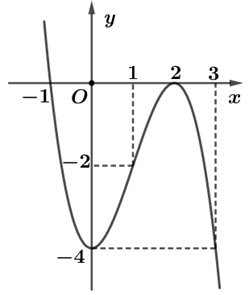
Câu 1
A. \(\left( {2; + \infty } \right)\).
Lời giải
Lời giải
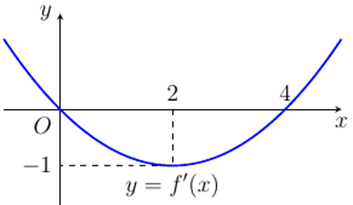
Từ đồ thị hàm số ta thấy hàm số \(y = f\left( x \right)\) đồng biến khoảng \(\left( {0\,;\,2} \right)\). Vậy hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {0;1} \right)\). Chọn D.
Câu 2
A. \[0\].
Lời giải
Lời giải
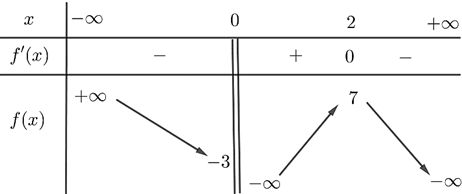
Từ bảng biến thiên ta thấy giá trị cực đại của hàm số bằng \(5\). Chọn B.
Câu 3
A. \(\frac{{14}}{3}\).
Lời giải
Lời giải
Từ bảng biến thiên ta thấy giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 10;10} \right]\) là \( - 38\) tại \[x = - 3\].
Chọn B.
Câu 4
A. \(y = - 1\).
Lời giải
Lời giải
Đồ thị hàm số đã cho có đường tiệm cận đứng là \(x = - \frac{1}{3}\). Chọn D.
Câu 5
A. \(x = - \frac{1}{2}\).
Lời giải
Lời giải
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2 - x}}{{2x + 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{2}{x} - 1}}{{2 + \frac{1}{x}}} = - \frac{1}{2}\); \(\mathop {\lim }\limits_{x \to - \infty } \frac{{2 - x}}{{2x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{\frac{2}{x} - 1}}{{2 + \frac{1}{x}}} = - \frac{1}{2}\).
Nên tiệm cận ngang của đồ thị hàm số \(y = \frac{{2 - x}}{{2x + 1}}\) là \(y = - \frac{1}{2}\). Chọn C.
Câu 6
A. \(\left( { - 1;\;3} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
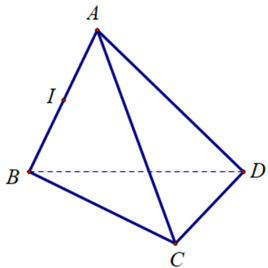
A. \(\overrightarrow {CD} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \[45^\circ \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. \(y = \frac{{ - x + 2}}{{x - 1}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
B. TRẮC NGHIỆM ĐÚNG - SAI. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\).
a) Hàm số đã cho đồng biến trên \[\left( { - \infty ; - 1} \right)\] và \(\left( {3; + \infty } \right)\).
b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng \( - 4\).
c) Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm \(A\left( {0;1} \right)\).
d) Phương trình tiếp tuyến của đồ thị hàm số đã cho vuông góc với đường thẳng \(x - 3y - 6 = 0\) đi qua điểm \(B\left( { - \frac{3}{2};\frac{3}{2}} \right)\).
B. TRẮC NGHIỆM ĐÚNG - SAI. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\).
a) Hàm số đã cho đồng biến trên \[\left( { - \infty ; - 1} \right)\] và \(\left( {3; + \infty } \right)\).
b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng \( - 4\).
c) Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm \(A\left( {0;1} \right)\).
d) Phương trình tiếp tuyến của đồ thị hàm số đã cho vuông góc với đường thẳng \(x - 3y - 6 = 0\) đi qua điểm \(B\left( { - \frac{3}{2};\frac{3}{2}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số \[f\left( x \right)\] có bảng biến thiên như sau: Giá trị cực đại của hàm số đã cho bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/08/blobid1-1756171387.png)
![Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình dưới đây. Khi đó giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 10;10} \right]\) bằng bao nhiêu? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/08/blobid2-1756171432.png)

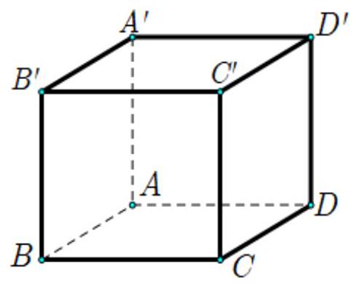
![Cho hình lập phương\[ABCD.A'B'C'D'\]. Số đo góc \[\left( {\overrightarrow {BC} ,\overrightarrow {B'D'} } \right)\] bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/08/blobid8-1756171733.png)
![Cho hàm số \[y = f\left( x \right)\] xác định trên \[\mathbb{R}\backslash \left\{ 1 \right\}\], liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau: Bảng biến thiên trên của hàm số nào trong các hàm số sau? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/08/blobid10-1756171849.png)