10 Bài tập Chứng minh hai vectơ cùng phương (có lời giải)
34 người thi tuần này 4.6 207 lượt thi 10 câu hỏi 45 phút
🔥 Đề thi HOT:
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
100 câu trắc nghiệm Mệnh đề - Tập hợp nâng cao (P1)
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
10 Bài tập Tính số trung bình, trung vị, tứ phân vị và mốt của mẫu số liệu cho trước (có lời giải)
15 câu Trắc nghiệm Toán 10 Cánh diều Mệnh đề toán học có đáp án
7 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề (Nhận biết) có đáp án
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có:
Vì – 2 < 0
Do đó, và cùng phương, ngược hướng.
Lời giải
Hướng dẫn giải:
Đáp án đúng là: B.
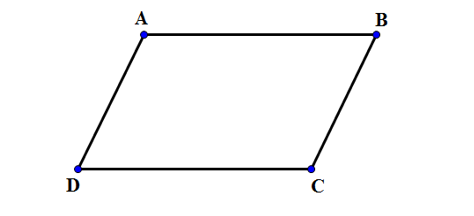
Xét hình bình hành ABCD có:
AB // CD
Do đó, và cùng phương, ngược hướng.
Lời giải
Hướng dẫn giải:
Đáp án đúng là: C.

Vì ABCD là hình vuông nên và cùng phương, ngược hướng; và cùng phương, ngược hướng.
Lại có và có cùng giá là đường thẳng AC.
Do đó, và cùng phương.
Vậy đáp án C sai.
Lời giải
Hướng dẫn giải:
Đáp án đúng là: C.
Ta có:
Vì – 2 < 0
Vậy , cùng phương, ngược hướng.
Lời giải
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có:
Giả sử tồn tại số thực k sao cho .
Mà và không cùng phương nên ta có:
Vậy không tồn tại k thỏa mãn.
Do đó, và không cùng phương.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.