10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
72 người thi tuần này 4.6 658 lượt thi 10 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Câu 1
A. 12,8;
B. 5;
C. 1,4;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: D
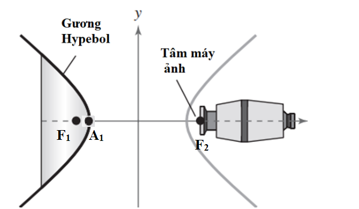
Gọi có a2 = 25 và b2 = 16.
Suy ra .
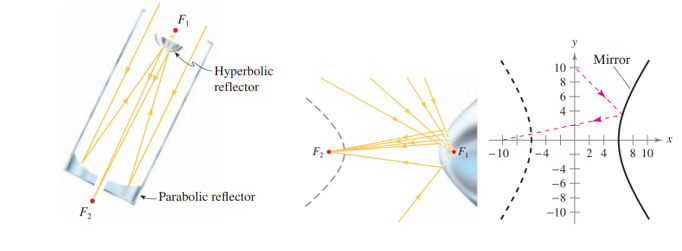
Ta tìm được một tiêu điểm của gương là và đỉnh của gương là A1(–5; 0).
Vậy khoảng cách từ tâm của máy ảnh tới đỉnh của gương là
Câu 2
A. M(6,54; 3,65);
B. M(6,54; 3,55);
C. M(– 32,25; 42,25);
Lời giải
Hướng dẫn giải:
Đáp án đúng là: B
Gọi
Phương trình của gương (H) có dạng , với a = 6, b = 8;
Suy ra .
Giả sử điểm cần tìm là M ∈ (H).
Gọi đường đi của ánh sáng qua điểm (0; 10) và M là d, do tia sáng sau khi phản xạ bởi gương sẽ đi qua tiêu điểm F1(–10; 0), suy ra d nhằm vào tiêu điểm F2(10; 0) (F2 ∈ d).
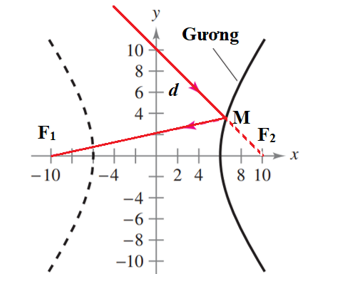
Từ đây dễ dàng lập được phương trình của d là y = –x + 10.
Tọa độ của M ∈ (H) là nghiệm của hệ:
Do điểm cần tìm nằm ở nhánh bên phải nên ta có M(6,54; 3,55).
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A
Gọi đường đi của con tàu là (H) thì (H) có phương trình dạng (a, b > 0).
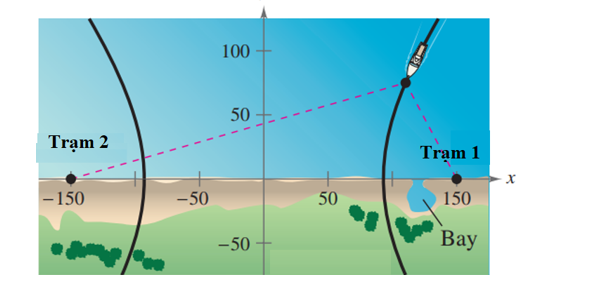
Với giả thiết ta có các tiêu điểm của (H) là F1(–150; 0) và F2(150; 0), suy ra c = 150.
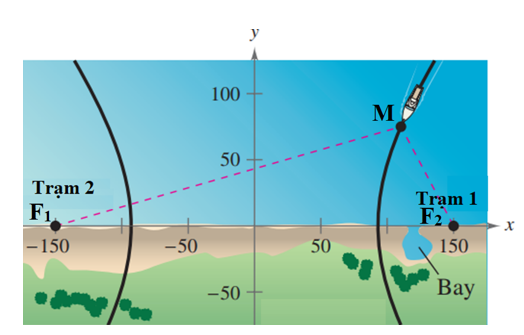
Giả sử vị trí con tàu hiện tại là M(x0; 75) ∈ (H); theo giả thiết độ chênh lệch thời gian giữa các xung từ các trạm phát là 1 000 micro giây (0,001 giây), tức là ta có |MF1 – MF2| = 0,001.186 000 = 186 (dặm); tức là ta có 2a = 186 suy ra a = 93.
Do đó
Phương trình (H) là: .
Ta có M(x0; 75) ∈ (H) .
Vậy hoành độ của con tàu gần bằng 110,2789.
Lời giải
Hướng dẫn giải:
Đáp án đúng là: B
Gọi đường đi của con tàu là (H) thì (H) có phương trình dạng (a, b > 0).
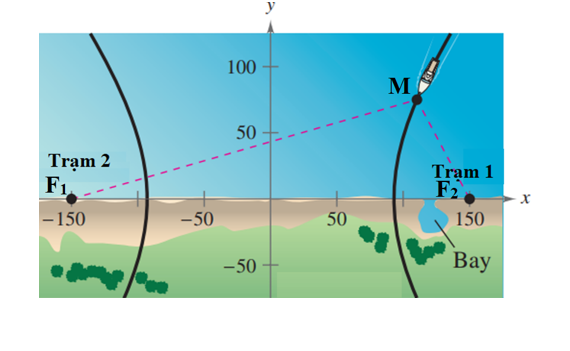
Với giả thiết ta có các tiêu điểm của (H) là F1(–150; 0) và F2(150; 0), suy ra c = 150.
Giả sử vị trí con tàu hiện tại là M(x0; 75) ∈ (H); theo giả thiết độ chênh lệch thời gian giữa các xung từ các trạm phát là 1 000 micro giây (0,001 giây), tức là ta có |MF1 – MF2| = 0,001.186 000 = 186 (dặm); tức là ta có 2a = 186 suy ra a = 93.
Do đó
Phương trình (H) là: .
Trạm phát số 1 nằm tại tiêu điểm F2(150; 0), vị trí khi con tàu vào bờ là đỉnh của (H) là A2(93; 0).
Vậy khoảng cách từ vị trí tàu vào bờ đến trạm số 1 là: F2A2 = 150 – 93 = 57 (dặm).
Câu 5
A. 107,89 km;
B. 167,89 km;
C. 136,01 km;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A
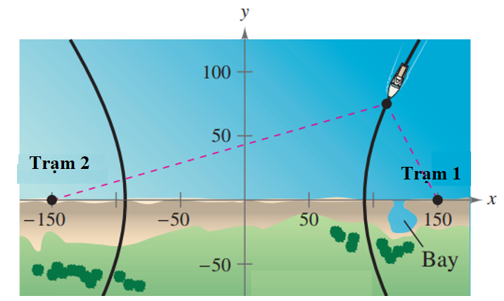
Gọi d1 và d2 là các khoảng cách tương ứng từ con tàu tới S1 và S2, khi đó hiệu d1 – d2 = 60 và con thuyền phải nằm trên một hyperbol với tiêu điểm là S1 và S2, hiệu hai khoảng cách cố định bằng 60 (Hình vẽ).
Để đưa ra phương trình của hyperbol, ta biểu diễn hiệu cố định này bằng 2a.
Như vậy, ta có c = 110,
Phương trình của hyperbol này có dạng là .
Thay y = 80 vào phương trình và giải theo x ta được:
Do đó x ≈ 37,61 (nghiệm âm bị loại, vì con tàu ở gần S2 hơn S1).
Khoảng cách từ con tàu đến S2 là km.
Câu 6
A. 2 200;
B. 4 800;
C. 5 280;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 75,00 km;
B. 66,14 km;
C. 100,00 km;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. (0; 10);
B. (0 ; 5);
C. (10; 0);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.