10 Bài tập Khoảng cách giữa hai đường thẳng chéo nhau (có lời giải)
48 người thi tuần này 4.6 415 lượt thi 10 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 1
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 3
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 2
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 1
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 3
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 2
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 1
Đề kiểm tra Hai mặt phẳng vuông góc (có lời giải) - Đề 3
Danh sách câu hỏi:
Câu 1
Lời giải
Đáp án đúng là: D
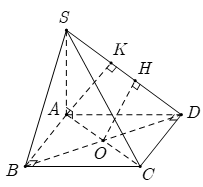
Vì SA ^ (ABCD) nên SA ^ AB mà AB ^ AD Þ AB ^ (SAD) Þ AB ^ AK.
Nếu AK ^ AC mà AB ^ AK Þ AK ^ (ABC) Þ AK º SA vì SA ^ (ABC).
Þ SA ^ SD Þ DSAD có hai góc vuông (vô lý). Suy ra đáp án A sai.
Vì ABCD là hình vuông AC và CD không vuông góc với nhau. Do đó đáp án B sai.
Nếu AC ^ OH mà AC ^ BD nên AC ^ (SBD) Þ AC ^ SO
Þ DSOA có hai góc vuông (vô lý).
Do đó đáp án C sai.
Lời giải
Đáp án đúng là: C
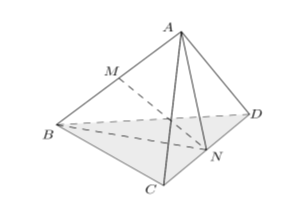
Gọi M, N lần lượt là trung điểm của AB và CD.
Vì các DACD, DBCD đều nên .
Do đó DANB cân tại N, suy ra MN ^ AB
Chứng minh tương tự ta có MN ^ CD, nên d(AB, CD) = MN.
Vì M là trung điểm của AB nên .
Xét DAMN vuông tại M, có .
Lời giải
Đáp án đúng là: D
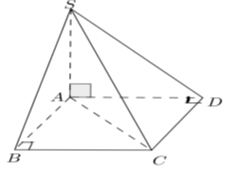
Vì SA ^ (ABCD) Þ SA ^ CD mà CD ^ AD Þ CD ^ (SAD) Þ CD ^ SD (1).
Mặt khác BC ^ CD (2).
Từ (1), (2), ta có CD là đoạn vuông góc chung của BC và SD.
Do đó d(BC, SD) = CD = AB (do ABCD là hình chữ nhật).
Xét DABC vuông tại B, có .
Lời giải
Đáp án đúng là: C
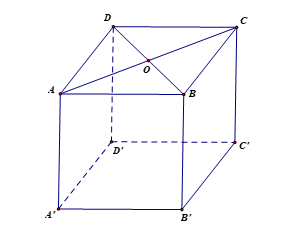
Gọi O là tâm của hình vuông ABCD nên O là trung điểm của AC, BD.
Vì ABCD là hình vuông nên AC ^ BD tại O.
Do đó BO ^ AC (1).
Mà BB' ^ (ABCD) Þ BB' ^ BO (2).
Từ (1) và (2), ta có BO là đoạn vuông góc chung của AC và BB'.
Do đó d(AC, BB') = BO.
Mà .
Do đó d(AC, BB') = .
Lời giải
Đáp án đúng là: B
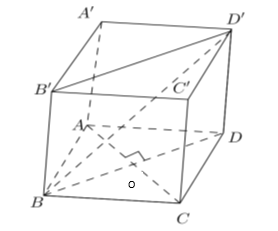
Vì AA' // BB' nên AA' // (BB'D'D).
Do đó d(AA', BD') = d(AA', (BB'D'D)) = d(A, (BB'D'D)).
Gọi O là tâm hình vuông ABCD.
Vì ABCD là hình vuông nên AO ^ BD mà BB' ^ AO (do BB' ^ (ABCD)).
Suy ra AO ^ (BB'D'D).
Do đó d(A, (BB'D'D)) = AO .
Câu 6
Cho khối lập phương ABCD.A'B'C'D'. Đoạn vuông góc chung của hai đường thẳng chéo nhau AD và A'C' là:
Cho khối lập phương ABCD.A'B'C'D'. Đoạn vuông góc chung của hai đường thẳng chéo nhau AD và A'C' là:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.