20 câu trắc nghiệm Toán 11 Chân trời sáng tạo Bài 1. Hai đường thẳng vuông góc (Đúng sai - Trả lời ngắn) có đáp án
59 người thi tuần này 4.6 230 lượt thi 20 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 1
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 3
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 2
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 1
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 3
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 2
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 1
Đề kiểm tra Hai mặt phẳng vuông góc (có lời giải) - Đề 3
Danh sách câu hỏi:
Câu 1
Lời giải
D
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Câu 2
Lời giải
D
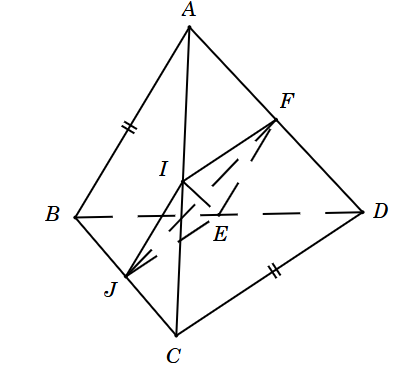
Ta có IF là đường trung bình của DACD \( \Rightarrow \left\{ \begin{array}{l}IF//CD\\IF = \frac{1}{2}CD\end{array} \right.\).
Lại có JE là đường trung bình của DBCD \( \Rightarrow \left\{ \begin{array}{l}JE//CD\\JE = \frac{1}{2}CD\end{array} \right.\).
Suy ra \(\left\{ \begin{array}{l}IF = JE\\IF//JE\end{array} \right.\) Þ tứ giác IJEF là hình bình hành.
Lại có \(\left\{ \begin{array}{l}IJ = \frac{1}{2}AB\\JE = \frac{1}{2}CD\end{array} \right.\) mà AB = CD nên IJ = JE.
Do đó IJEF là hình thoi. Suy ra (IE, JF) = 90°.
Câu 3
Lời giải
D
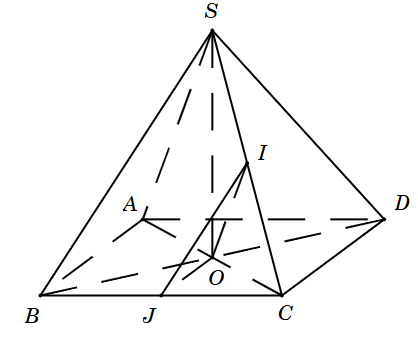
Gọi O là tâm của hình thoi ABCD Þ OJ là đường trung bình của DBCD.
Suy ra \(\left\{ \begin{array}{l}OJ//CD\\OJ = \frac{1}{2}CD\end{array} \right.\).
Vì CD // OJ Þ (IJ, CD) = (IJ, OJ).
Vì \(IJ = \frac{1}{2}SB = \frac{a}{2};OJ = \frac{1}{2}CD = \frac{a}{2};OI = \frac{1}{2}SA = \frac{a}{2}\) nên DIOJ đều.
Suy ra (IJ, CD) = (IJ, OJ) = \(\widehat {IJO} = 60^\circ \).
Câu 4
Lời giải
D
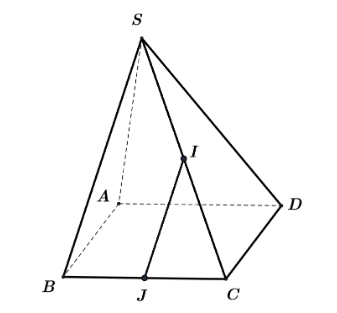
Ta có IJ là đường trung bình của DSBC nên IJ // SB.
Vì IJ // SB và CD // AB nên (IJ, CD) = (SB, AB) = \(\widehat {SBA} = 60^\circ \) (do DSAB đều).
Câu 5
Lời giải
D
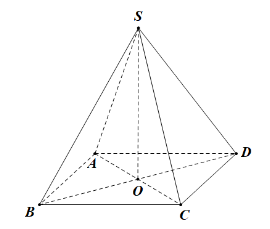
Vì AB // CD nên (SA, CD) = (SA, AB).
Tam giác SAB đều cạnh a \( \Rightarrow \widehat {SAB} = 60^\circ \). Vậy (SA, CD)= 60°.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.