20 câu trắc nghiệm Toán 11 Chân trời sáng tạo Bài 5. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện (Đúng sai - Trả lời ngắn) có đáp án
48 người thi tuần này 4.6 215 lượt thi 20 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 1
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 3
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 2
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 1
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 3
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 2
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 1
Đề kiểm tra Hai mặt phẳng vuông góc (có lời giải) - Đề 3
Danh sách câu hỏi:
Câu 1
Lời giải
B
Ta có O là hình chiếu vuông góc của S xuống mặt phẳng (ABCD) nên góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng góc \(\widehat {SBO}\).
Câu 2
Lời giải
A
Ta có (AC', (ABCD)) = (AC', AC) = \(\widehat {C'AC} = \alpha \).
Giả sử hình lập phương có cạnh là a.
Trong DCC'A ta có \(\sin \alpha = \frac{{CC'}}{{AC'}} = \frac{a}{{\sqrt {2{a^2} + {a^2}} }} = \frac{{\sqrt 3 }}{3}\).
Câu 3
A. \(\frac{{\sqrt 2 }}{2}\).
Lời giải
D
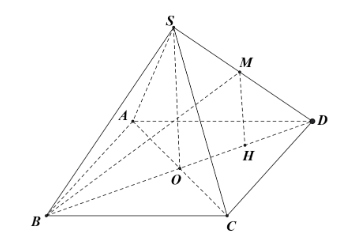
Gọi O là tâm của hình vuông, hạ MH ^ BD.
Ta có SO ^ (ABCD) và \(SO = \sqrt {{a^2} - \frac{{{a^2}}}{2}} = \frac{{a\sqrt 2 }}{2}\).
Gọi M là trung điểm của OD ta có MH // SO nên H là hình chiếu của M lên mặt phẳng (ABCD) và \(MH = \frac{1}{2}SO = \frac{{a\sqrt 2 }}{4}\).
Do đó góc giữa đường thẳng BM và mặt phẳng (ABCD) là \(\widehat {MBH}\).
Khi đó ta có \(\tan \widehat {MBH} = \frac{{MH}}{{BH}} = \frac{{a\sqrt 2 }}{4}:\frac{{3a\sqrt 2 }}{4} = \frac{1}{3}\).
Lời giải
B
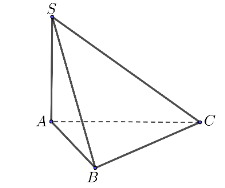
Vì SA ^ (ABC) nên AB là hình chiếu của SB trên mặt phẳng (ABC).
Do đó (SB, (ABC)) = (SB, AB) = \(\widehat {SBA}\).
Xét DSAB vuông tại A, có SA = AB = \(a\sqrt 2 \) Þ DSAB vuông cân tại A Þ \(\widehat {SBA} = 45^\circ \).
Lời giải
A
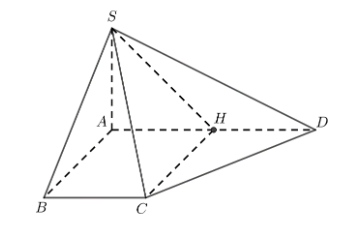
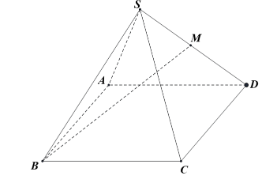
Gọi H là trung điểm của AD Þ AH = HD = a.
Vì BC // AH và BC = AH nên ABCH là hình bình hành mà \(\widehat A = 90^\circ \) nên ABCH là hình chữ nhật.
Suy ra CH ^ AD mà CH ^ SA (SA ^ (ABCD)) Þ CH ^ (SAD).
Khi đó SH là hình chiếu của SC lên mặt phẳng (SAD).
Suy ra góc giữa SC và (SAD) là góc \(\widehat {CSH}\).
Tam giác SHC vuông tại H và có CH = a, \(SH = \sqrt {S{A^2} + A{H^2}} = a\sqrt 3 \).
Ta có \(\tan \widehat {CSH} = \frac{{CH}}{{SH}} = \frac{a}{{\sqrt {{a^2} + 2{a^2}} }} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {CSH} = 30^\circ \).
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
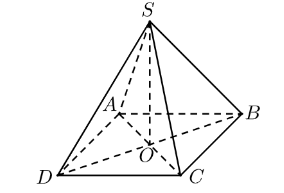
![Xác định góc nhị diện [A, CD, B]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/8-1751859922.png)
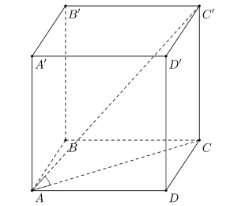
![Tìm góc phẳng nhị diện [A, B'D', A'] (tính theo độ, làm tròn kết quả đến hàng phần mười). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/18-1751860356.png)