Đề cương ôn tập giữa kì 1 Toán 11 Chân trời sáng tạo cấu trúc mới có đáp án - Bài 4: Hàm số lượng giác và đồ thị
27 người thi tuần này 4.6 1.2 K lượt thi 13 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 1
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 3
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 2
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 1
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 3
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 2
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 1
Đề kiểm tra Hai mặt phẳng vuông góc (có lời giải) - Đề 3
Danh sách câu hỏi:
Câu 1
Lời giải
Hàm số \(y = \sin x\) có tập xác định là \(\mathbb{R}\). Chọn B.
Câu 2
Lời giải
Các hàm số \(y = \sin x,y = \tan x,y = \cot x\) là hàm số lẻ. Chọn B.
Hàm số \(y = \cos x\) là hàm số chẵn.
Câu 3
Lời giải
Dựa vào đồ thị, ta thấy hàm số đồng biến trên \[\left( { - \frac{\pi }{2};0} \right).\] Chọn D.
Câu 4
Lời giải
Hàm số \(y = \tan x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi \,|k \in \mathbb{Z}} \right\}\). Chọn A.
Câu 5
Lời giải
Hàm số \(y = \cot \left( {2x - \frac{\pi }{3}} \right)\) xác định khi \(\sin \left( {2x - \frac{\pi }{3}} \right) \ne 0\)\( \Leftrightarrow 2x - \frac{\pi }{3} \ne k\pi \)\( \Leftrightarrow x \ne \frac{\pi }{6} + k\frac{\pi }{2},k \in \mathbb{Z}\).
Vậy tập xác định của hàm số là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{6} + k\frac{\pi }{2}\,|k \in \mathbb{Z}} \right\}\). Chọn D.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hàm số \(y = \cos x\).
a) Hàm số đã cho có tập xác định là \(D = \left[ { - 1;1} \right]\).
b) Đồ thị hàm số đã cho đi qua điểm \(A\left( {0;1} \right)\).
c) Đồ thị hàm số đã cho nhận trục tung làm trục đối xứng.
d) Hàm số đã cho nghịch biến trên khoảng \(\left( {0;\frac{{3\pi }}{2}} \right)\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hàm số \(y = \cos x\).
a) Hàm số đã cho có tập xác định là \(D = \left[ { - 1;1} \right]\).
b) Đồ thị hàm số đã cho đi qua điểm \(A\left( {0;1} \right)\).
c) Đồ thị hàm số đã cho nhận trục tung làm trục đối xứng.
d) Hàm số đã cho nghịch biến trên khoảng \(\left( {0;\frac{{3\pi }}{2}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Cho hàm số \(y = \sin x\) có đồ thị như hình
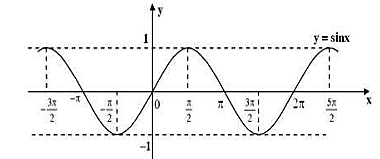
a) Hàm số \(y = \sin x\) nghịch biến trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\) và đồng biến trên khoảng \(\left( {\frac{\pi }{2};\pi } \right)\).
b) Trên khoảng \(\left( { - \frac{\pi }{2};\frac{{5\pi }}{2}} \right)\) có 3 giá trị của \(x\) để \(\sin x = 0\).
c) Đường thẳng \(y = - 0,35\) giao với đồ thị hàm số \(y = \sin x\) tại 2 điểm phân biệt trên khoảng \(\left( { - \frac{\pi }{2};\frac{{3\pi }}{2}} \right)\).
d) Hàm số \(y = \sin x\) đồng biến trên khoảng \(\left( {\frac{\pi }{7};\frac{\pi }{5}} \right)\).
Cho hàm số \(y = \sin x\) có đồ thị như hình

a) Hàm số \(y = \sin x\) nghịch biến trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\) và đồng biến trên khoảng \(\left( {\frac{\pi }{2};\pi } \right)\).
b) Trên khoảng \(\left( { - \frac{\pi }{2};\frac{{5\pi }}{2}} \right)\) có 3 giá trị của \(x\) để \(\sin x = 0\).
c) Đường thẳng \(y = - 0,35\) giao với đồ thị hàm số \(y = \sin x\) tại 2 điểm phân biệt trên khoảng \(\left( { - \frac{\pi }{2};\frac{{3\pi }}{2}} \right)\).
d) Hàm số \(y = \sin x\) đồng biến trên khoảng \(\left( {\frac{\pi }{7};\frac{\pi }{5}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.