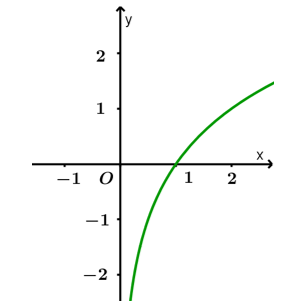
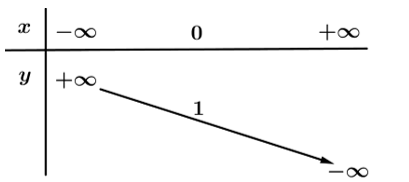
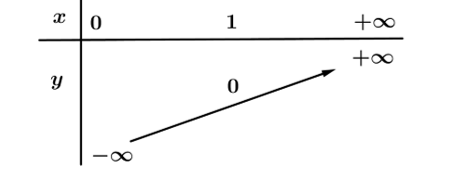
Đề kiểm tra Hàm số mũ - hàm số lôgarit (có lời giải)- Đề 2
16 người thi tuần này 4.6 57 lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Phép tính lôgarit (có lời giải) - Đề 2
0 lượt thi
22 câu hỏi
Đề kiểm tra Phép tính lôgarit (có lời giải) - Đề 1
0 lượt thi
22 câu hỏi
Đề kiểm tra Phép tính lũy thừa (có lời giải) - Đề 3
62 lượt thi
22 câu hỏi
Đề kiểm tra Phép tính lũy thừa (có lời giải) - Đề 2
66 lượt thi
22 câu hỏi
Đề kiểm tra Phép tính lũy thừa (có lời giải) - Đề 1
80 lượt thi
22 câu hỏi
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 10
2.8 K lượt thi
38 câu hỏi
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 8
2.7 K lượt thi
38 câu hỏi
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 7
2.7 K lượt thi
38 câu hỏi
Danh sách câu hỏi:
Câu 1
A. \[y = \log _3^{}x\].
B. \[y = {x^2}\].
C. \[y = {\left( {\sqrt 2 } \right)^x}\].
D. \[y = {x^{\sqrt 7 }}\].
Lời giải
Ta có: \[y = {\left( {\sqrt 2 } \right)^x}\] là hàm số mũ.
Câu 2
A. \[y = \log _3^{}x\].
B. \[y = {x^2}\].
C. \[y = {\left( {\sqrt 2 } \right)^x}\].
D. \[y = {x^{\sqrt 7 }}\].
Lời giải
Ta có: \[y = {\left( {\sqrt 2 } \right)^x}\] là hàm số lôgarit.
Câu 3
A. \[\left[ {0\,;\, + \infty } \right)\].
B. \[\left( { - \infty \,;\, + \infty } \right)\].
C. \[\left( {0\,;\, + \infty } \right)\].
D. \[\left( {3\,;\, + \infty } \right)\].
Lời giải
Hàm số \[y = {\log _2}\left( {x - 3} \right)\]có nghĩa khi: \[x - 3 > 0 \Leftrightarrow x > 3\]
Tập xác định của hàm số là: \[\left( {3\,;\, + \infty } \right)\].Câu 4
A. \[\left[ {5\,;\, + \infty } \right)\].
B. \[\left( { - \infty \,;\, + \infty } \right)\].
C. \[\left( {0\,;\, + \infty } \right)\].
D. \[\left( {5\,;\, + \infty } \right)\].
Lời giải
Hàm số \[y = {\left( {\sqrt 5 } \right)^x}\]có nghĩa \(\forall x \in \mathbb{R}\).
Tập xác định của hàm số là: \[\left( { - \infty \,;\, + \infty } \right)\].
Câu 5
A. \(y = {3^x}\).
B. \(y = {\left( {\frac{1}{3}} \right)^x}\).
C. \(y = {\log _{\frac{1}{3}}}x\).
D. \(y = {\log _3}x\).
Lời giải
Hàm số có đồ thị như hình vẽ trên nghịch biến trên \(\left( { - \infty ; + \infty } \right)\) nên loại A, D, đồ thị nhận \(Ox\) làm tiệm cận ngang chọn hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\).
Câu 6
A. \(y = {2^x}\).
B. \(y = {\left( {\frac{1}{2}} \right)^x}\).
C. \(y = {\log _{\frac{1}{2}}}x\).
D. \(y = {\log _2}x\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(y = \log x\).
B. \(y = {\left( {\frac{{\sqrt 2 }}{5}} \right)^x}\).
C. \(y = \ln x\).
D. \(y = {\left( {\frac{1}{7}} \right)^{ - x}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. Hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).
B. Hàm số đồng biến trên \(\left( { - \infty ; + \infty } \right)\).
C. Đồ thị hàm số có đường tiệm cận ngang là trục hoành.
D. Đồ thị hàm số đi qua điểm \(A\left( {0;1} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \[y = {3^x}\].
B. \[y = {\left( {\frac{1}{2}} \right)^x}\].
C. \[y = \log x\].
D. \[y = {\log _{\left( {\frac{1}{5}} \right)}}x\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \[y = {3^x}\].
B. \[y = {\left( {\frac{1}{5}} \right)^x}\].
C. \[y = {\log _3}x\].
D. \[y = {\log _{\left( {\frac{1}{5}} \right)}}x\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. \(2038\).
B. \(2039\).
C. \(2040\).
D. \(2041\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \(46794000\) đồng
B. \(44163000\) đồng
C. \(42465000\) đồng
D. \(41600000\) đồng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
a) Hàm số có tập xác định \(D = \mathbb{R}\)
Đúng
Sai
b) Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
Đúng
Sai
c) Hàm số đi qua điểm \(A\left( {\frac{1}{4}; - 1} \right)\)
Đúng
Sai
d) Đồ thị hàm số cắt đường thẳng \(y = 1\) tại điểm có hoành độ bằng \(3\)
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
a) \({\log _2}3 > {\log _2}\frac{5}{2}\)
Đúng
Sai
b) \({\log _{\frac{1}{e}}}2 > {\log _{\frac{1}{e}}}\frac{5}{4}\)
Đúng
Sai
c) \({\left( {\frac{1}{3}} \right)^{4000}} > {\left( {\frac{1}{3}} \right)^{3999}}\)
Đúng
Sai
d) \({\pi ^{{n^2}}} > {\pi ^{{n^2} - 1}}\)
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
a) \(y = {\log _{\frac{1}{8}}}x\)có tập xác định hàm số là \(D = (0; + \infty )\).
Đúng
Sai
b) \(y = \ln \frac{1}{{{x^2}}}\) có tập xác định hàm số là: \(D = \mathbb{R}\backslash \{ 0\} \).
Đúng
Sai
c) \(y = {e^{2x}}\) có tập xác định hàm số là \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
Đúng
Sai
d) \(y = \frac{{{6^x}}}{{\log x}} + \log \left( {{x^2} - x} \right)\) có tập xác định hàm số là \(D = {\rm{[}}1; + \infty )\).
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
a) \({a^{\sqrt 2 }} < {a^{\sqrt 3 }}\) suy ra \(a > 1\)
Đúng
Sai
b) \({\log _b}30 < {\log _b}29,7\) suy ra \(0 < b < 1\)
Đúng
Sai
c) \({a^{\frac{{\sqrt 3 }}{4}}} > {a^{\frac{{\sqrt 2 }}{3}}}\) suy ra \(a < 1\)
Đúng
Sai
d) \({\log _b}7 < {\log _b}2\) suy ra \(b > 1\)
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập