(Trả lời ngắn) 4 bài tập Phương trình đường thẳng trong không gian (có lời giải)
75 người thi tuần này 4.6 215 lượt thi 4 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Lời giải
Đáp án: \[P = 0\]
Ta có \[d{\rm{//}}\Delta \].
Chọn \[A\left( {2;\, - 1;\,1} \right) \in \left( d \right),\,B\left( {3;\, - 2;\,1} \right) \in \left( \Delta \right)\].
\[\overrightarrow {AB} = \left( {1;\, - 1;\,0} \right)\]
Phương trình mặt phẳng chứa hai đường thẳng \[\left( d \right)\] và \[\left( \Delta \right)\] qua \[A\left( {2;\, - 1;\,1} \right)\] và có VTPT \[\overrightarrow n = \left[ {\overrightarrow {AB} ,\,\overrightarrow {{u_{\left( d \right)}}} } \right] = \left( { - 2;\, - 2;\,4} \right) = - 2\left( {1;\,1;\, - 2} \right)\] là:
\[1\left( {x - 2} \right) + 1\left( {y + 1} \right) - 2\left( {z - 1} \right) = 0 \Leftrightarrow x + y - 2z + 1 = 0\].
Lời giải
Đáp án: \[h - k = 0\]
\[H \in {\Delta _1} \Leftrightarrow H\left( {3 + 2t;t;1 + t} \right)\].
\[K \in {\Delta _2} \Leftrightarrow K\left( {1 + m;2 + 2m;m} \right)\].
Ta có\[\overrightarrow {HK} = \left( {m - 2t - 2;2m - t + 2;m - t - 1} \right)\].
Đường thẳng \[d\] có một VTCP là \[\overrightarrow {{u_d}} = \left( {1;1; - 2} \right)\].
\[\Delta \bot d \Leftrightarrow \]\[\overrightarrow {{u_d}} .\overrightarrow {HK} = 0\]\[ \Leftrightarrow m - t + 2 = 0 \Leftrightarrow m = t - 2 \Rightarrow \overrightarrow {HK} = \left( { - t - 4;t - 2; - 3} \right).\]
Ta có\[H{K^2} = {\left( { - t - 4} \right)^2} + {\left( {t - 2} \right)^2} + {\left( { - 3} \right)^2} = 2{\left( {t + 1} \right)^2} + 27 \ge 27,\forall t \in \mathbb{R}\]
\[ \Rightarrow minHK = \sqrt {27} ,\]đạt được khi \[t = - 1\].
Khi đó ta có \[\overrightarrow {HK} = \left( { - 3; - 3; - 3} \right)\], suy ra \[\overrightarrow u \left( {1;1;1} \right) \Rightarrow h = k = 1 \Rightarrow h - k = 0.\]
Lời giải
Đáp án: \(d\left( {M\,,\,\left( {Oxy} \right)} \right) = 4\)
Gọi \(M\left( {x\,;\,y\,;\,z} \right)\) là điểm cần tìm.
\(\overrightarrow {AM} = \left( {x - 3\,;\,y - 1\,;\,z - 2} \right)\), \(\overrightarrow {BM} = \left( {x + 3\,;\,y + 1\,;\,z} \right)\).
Vì \(\Delta MAB\) vuông tại \(M\) nên \(\overrightarrow {AM} .\overrightarrow {BM} = 0 \Leftrightarrow \left( {x - 3} \right)\left( {x + 3} \right) + \left( {y - 1} \right)\left( {y + 1} \right) + z\left( {z - 2} \right) = 0\)
\[ \Leftrightarrow {x^2} - 9 + {y^2} - 1 + {z^2} - 2z = 0 \Leftrightarrow {x^2} + {y^2} + {\left( {z - 1} \right)^2} = 11\].
\( \Rightarrow M\) thuộc mặt cầu \(\left( S \right)\) có tâm \(I\left( {0\,;\,0\,;\,1} \right)\) và bán kính \(R = \sqrt {11} \).
Nhận xét thấy \(d\left( {I\,,\,\left( P \right)} \right) = \frac{{\left| {0 + 0 + 3.1 - 14} \right|}}{{\sqrt {{1^2} + {1^2} + {3^3}} }} = \sqrt {11} = R\).
\( \Rightarrow \left( P \right)\) tiếp xúc với \(\left( S \right)\) tại \(M\)
\( \Rightarrow M\) là hình chiếu vuông góc của \(I\) trên \(\left( P \right)\)
Vậy \(d\left( {M\,,\,\left( {Oxy} \right)} \right) = \left| 4 \right| = 4\).
Lời giải
Đáp án: khoảng cách từ \(A\)đến mặt phẳng \(\left( \alpha \right)\) bằng \(3\).
Đường thẳng \(d:\frac{{x - 5}}{2} = \frac{{y + 7}}{2} = \frac{{z - 12}}{{ - 1}}\) có một vectơ chỉ phương là \[\overrightarrow u = \left( {2\,;\,2\,;\, - 1} \right)\].
Mặt phẳng \(\left( \alpha \right):x + 2y - 3z - 3 = 0\)có một vectơ pháp tuyến là \[\overrightarrow n = \left( {1\,;\,2\,;\, - 3} \right)\].
Ta có: \[\sin \left( {d\,;\,\left( \alpha \right)} \right) = \frac{{\left| {\overrightarrow {{u_d}} \,.\,\overrightarrow {{n_\alpha }} } \right|}}{{\left| {\overrightarrow {{u_d}} } \right|\,.\,\left| {\overrightarrow {{n_\alpha }} } \right|}} = \frac{{3\sqrt {14} }}{{14}}\].
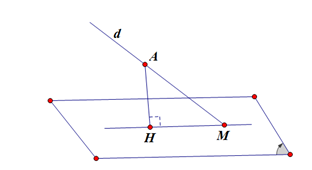
Gọi \[H\] là hình chiếu vuông góc của \(A\)lên mặt phẳng \(\left( \alpha \right)\).
Khi đó tam giác \(\Delta MAH\) vuông tại \[H\] nên \[\sin \left( {d\,;\,\left( \alpha \right)} \right) = \sin \widehat {AMH} = \frac{{AH}}{{AM}}\].
\[ \Rightarrow AH = AM\,.\,\sin \left( {d\,;\,\left( \alpha \right)} \right) = 3\].
Vậy khoảng cách từ \(A\)đến mặt phẳng \(\left( \alpha \right)\) bằng \(3\).