10 Bài tập Khoảng cách từ một điểm tới một đường thẳng, mặt phẳng (có lời giải)
42 người thi tuần này 4.6 469 lượt thi 10 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 1
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 3
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 2
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 1
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 3
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 2
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 1
Đề kiểm tra Hai mặt phẳng vuông góc (có lời giải) - Đề 3
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: B
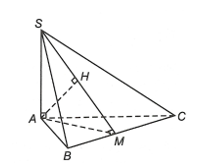
Gọi M là trung điểm BC, H là hình chiếu vuông góc của A trên SM.
Vì DABC đều nên AM ^ BC và .
Vì SA ^ (ABC) nên SA ^ BC mà AM ^ BC nên BC ^ (SAM) ⇒ BC ^ AH.
Lại có AH ^ SM do đó AH ^ (SBC) ⇒ d(A, (SBC)) = AH.
Xét DSAM vuông tại A, cóLời giải
Đáp án đúng là: A
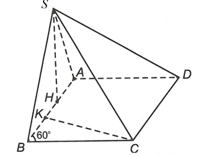
Dựng SH ^ AB. Do (SAB) ^ (ABCD) và (SAB) Ç (ABCD) = AB nên SH ^ (ABCD).
Dựng CK ^ AB.
Vì SH ^ (ABCD) ⇒ SH ^ CK mà CK ^ AB nên CK ^ (SAB).
Do CD // AB nên d(D, (SAB)) = d(C, (SAB)) = CK.
Xét DCKB vuông tại K, có CK = BC.sin60° = .
Lời giải
Đáp án đúng là: D
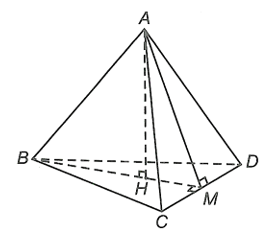
Gọi M là trung điểm CD và H là hình chiếu vuông góc của A trên BM.
Vì DBCD, DACD đều nên BM ^ CD, AM ^ CD.
Do đó CD ^ (ABM) ⇒ CD ^ AH.
Vì AH ^ BM và AH ^ CD nên AH ^ (BCD).
Do đó d(A, (BCD)) = AH.
Mà ABCD là tứ diện đều nên H là trọng tâm của DBCD.
Vì DBCD, DACD đều cạnh a nên và
Xét DAHM vuông tại H, có .
Lời giải
Đáp án đúng là: A
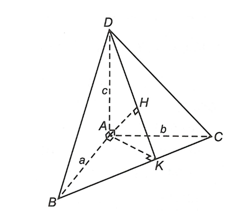
Kẻ AK ^ BC (K Î BC) và AH ^ DK (H Î DK)
Vì AD ^ AB, AD ^ AC nên AD ^ (ABC) ⇒ AD ^ BC.
Mà AK ^ BC. Do đó BC ^ (ADK) ⇒ BC ^ AH mà AH ^ DK nên AH ^ (BCD).
Do đó d(A, (BCD)) = AH.
Xét DABC vuông tại A có:
Xét DADK vuông tại A có:
Vậy
Lời giải
Đáp án đúng là: B
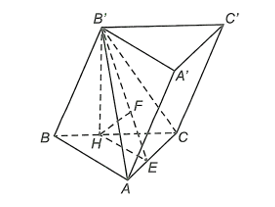
Xét DABC vuông tại A, có .
Xét DB'HB vuông tại H, có .
Kẻ HE ^ AC tại E, HF ^ B'E tại F.
Vì B'H ^ (ABC) ⇒ B'H ^ AC mà AC ^ HE nên AC ^ (B'HE) ⇒ AC ^ HF.
Mà HF ^ B'E nên HF ^ (B'AC).
Do đó d(H, (B'AC)) = HF.
Có HE // AB (vì cùng vuông góc với AC) nên .
Xét DB'HE vuông tại H, có .
Mặt khác Do đóLời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.