12 bài tập Một số bài toán thực tế liên quan đến tỉ số lượng giác của góc nhọn có lời giải
50 người thi tuần này 4.6 178 lượt thi 12 câu hỏi 45 phút
🔥 Đề thi HOT:
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
23 K lượt thi
3 câu hỏi
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
20 K lượt thi
20 câu hỏi
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
6.6 K lượt thi
5 câu hỏi
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
1.9 K lượt thi
16 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
3.7 K lượt thi
20 câu hỏi
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
20.6 K lượt thi
4 câu hỏi
123 bài tập Nón trụ cầu và hình khối có lời giải
1.4 K lượt thi
123 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: A
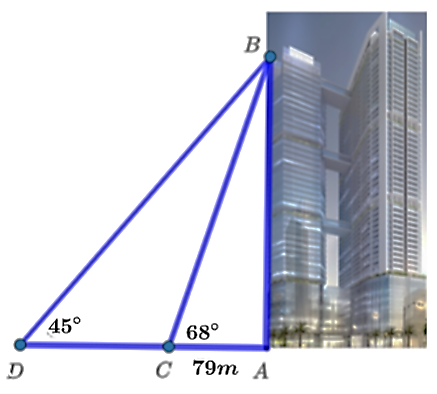
Chiều cao của tòa tháp chính là độ dài của đoạn AB.
Xét tam giác ABC vuông tại A, ta có: AB = AC. \(\tan \widehat {ACB}\) = 79.tan68° ≈ 196 m.
Sử dụng dữ kiện bài toán sau để trả lời Bài 2, 3.
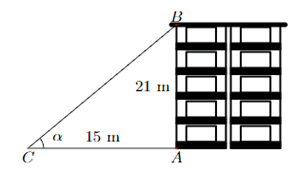
Tháp chung cư cư Discovery Complex A với quy mô 54 tầng, đang là tòa nhà cao nhất quận Cầu Giấy. Tại một thời điểm trong ngày, tia nắng mặt trời tạo với mặt đất một góc xấp xỉ 67° và bóng của tòa nhà trên mặt đất dài khoảng 72 m.
Lời giải
Đáp án đúng là: B
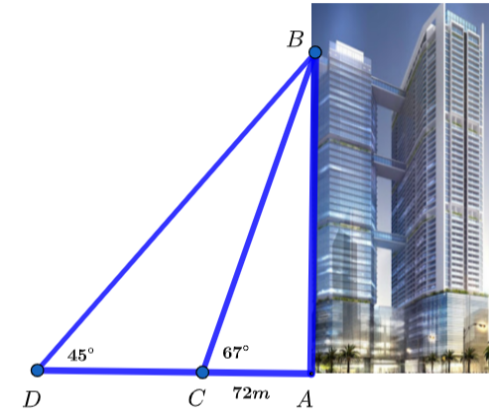
Chiều cao của tòa tháp chính là độ dài đoạn AB.
Xét tam giác ABC vuông tại A, ta có:
AB = AC.tan\(\widehat {ACB}\) = 72.tan67° ≈ 170 m.
Lời giải
Đáp án đúng là: B
Xét tam giác vuông ABD có: BD = \(\frac{{AB}}{{\sin \widehat {ADB}}} = \frac{{170}}{{\sin 45^\circ }} = 170\sqrt 2 \) (m).
Vận tốc trung bình của chiếc flycam đó là: \(170\sqrt 2 :140 \approx 1,72{\rm{ }}\left( {m/s} \right)\).
Vậy vận tốc trung bình của chiếc flycam đó khoảng 1,72 m/s.
Lời giải
Đáp án đúng là: C
Khoảng cách của cồn và bờ sông hai người đứng chính là độ dài đoạn thẳng CH.
Xét tam giác AHC vuông tại H, ta có:
\(\tan \widehat {CAH} = \frac{{CH}}{{AH}}\) nên \(AH = \frac{{CH}}{{\tan \widehat {CAH}}} = \frac{{CH}}{{\tan 43^\circ }}\). (1)
Xét tam giác BHC vuông tại H, ta có:
\(\tan \widehat {CBH} = \frac{{CH}}{{BH}}\) nên \(BH = \frac{{CH}}{{\tan \widehat {CBH}}} = \frac{{CH}}{{\tan 28^\circ }}\). (2)
Từ (1) và (2) ta có:
AB + AH + BH = \(\frac{{CH}}{{\tan 43^\circ }} + \frac{{CH}}{{\tan 28^\circ }} = CH\left( {\frac{1}{{\tan 43^\circ }} + \frac{1}{{\tan 28^\circ }}} \right)\)
Do đó, \(CH = \frac{{AB}}{{\frac{1}{{\tan 43^\circ }} + \frac{1}{{\tan 28^\circ }}}} = \frac{{250}}{{\frac{1}{{\tan 43^\circ }} + \frac{1}{{\tan 28^\circ }}}} \approx 84,66{\rm{ (m)}}{\rm{.}}\)
Vậy cồn cách bờ sông hai người đứng khoảng 84,66 m.
Lời giải
Đáp án đúng là: A
Xét tam giác ADC vuông tại C, ta có: AC = h.cot\(\widehat {DAC}\) = h.cot60° (m)
Xét tam giác BDC vuông tại C, ta có: BC = h.cot\(\widehat {DBC}\) = h.cot75° (m).
Do AC – BC = AB = 101 nên h.cot60° − h.cot75° = 101
Suy ra h = \(\frac{{101}}{{\cot 60^\circ - \cot 75^\circ }} \approx 326\) (m).
Vậy tháp Eiffel có độ cao khoảng 326 (m).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Sử dụng dữ kiện bài toán sau để trả lời cho Bài 4,5.
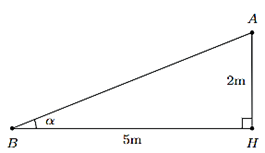
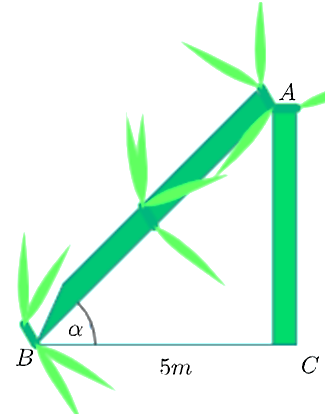
Sau một trận bão lớn, một cái cây mọc thẳng đứng ở cị trí C đã gãy ngang tại A (như hình vẽ). Ngọn cây chạm mặt đất cách gốc một khoảng BC = 5 m. Biết rằng phần ngọn bị gãy AB và phần gốc AC có tỉ lệ 3:2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Sử dụng dữ kiện của bài toán dưới đây để trả lời cho Bài 8, 9 , 10.
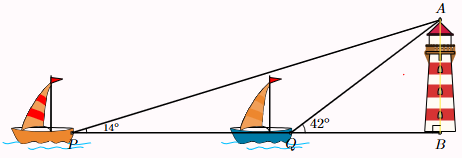
Hai con thuyền P và Q cách nhau 300 m và thẳng hàng với chân B của tháp hải đăng ở trên bờ biển. Từ P và Q, người ta nhìn thấy tháp hải đăng dưới các góc \(\widehat {BPQ} = 14^\circ \) và \(\widehat {BQA} = 42^\circ \). Đặt h = AB là chiều cao của tháp hải đăng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
4.6
36 Đánh giá
50%
40%
0%
0%
0%