Bộ 10 đề thi giữa kì 2 Toán 9 Kết nối tri thức có đáp án - Đề 08
22 người thi tuần này 4.6 5.7 K lượt thi 5 câu hỏi 45 phút
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 1: Đại số)
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
Bộ 10 đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 1
Trắc nghiệm Bài tập lý thuyết Liên hệ giữa phép nhân, phép chia và phép khai phương có đáp án
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
1. a) Trong các phương trình trên, phương trình bậc hai một ẩn là: \( - {x^2} - 7x - 6 = 0;\)\({x^2} - 2\sqrt 2 x + 2 = 0\).
• Với phương trình \( - {x^2} - 7x - 6 = 0,\) ta có \(a = - 1,b = - 7,c = - 6\).
• Với phương trình \({x^2} - 2\sqrt 2 x + 2 = 0\), ta có \(a = 1,b = 2\sqrt 2 ,c = 2\).
b) • Giải phương trình \( - {x^2} - 7x - 6 = 0,\) ta thấy \(a - b + c = 1 - \left( { - 7} \right) + 6 = 0\) nên phương trình có hai nghiệm \(x = - 1\) và \(x = - 6\).
Vậy phương trình có nghiệm là \(\left\{ { - 1; - 6} \right\}\).
• Giải phương trình \({x^2} - 2\sqrt 2 x + 2 = 0\), ta được: \({x^2} - 2\sqrt 2 x + 2 = 0\) hay \({\left( {x - \sqrt 2 } \right)^2} = 0\)
Suy ra \(x - \sqrt 2 = 0\) nên \(x = \sqrt 2 \).
Vậy phương trình có nghiệm là \(\left\{ {\sqrt 2 } \right\}\).
2. Gọi khối lượng riêng của miếng kim loại thứ nhất là \(x\) (g/cm3) \(\left( {x > 1} \right).\)
Khối lượng riêng của miếng kim loại thứ hai là \(x - 1\) (g/cm3).
Thể tích của miếng kim loại thứ nhất là: \(\frac{{880}}{x}\) (cm3).
Thể tích của miếng kim loại thứ hai là: \(\frac{{858}}{{x - 1}}\) (cm3).
Theo đề bài, thể tích của miếng thứ nhất nhỏ hơn thể tích của miếng thứ hai là 10 cm3 nên ta có phương trình: \(\frac{{858}}{{x - 1}} - \frac{{880}}{x} = 10.\)
Giải phương trình:
\(\frac{{858}}{{x - 1}} - \frac{{880}}{x} = 10\)
\(\frac{{858x}}{{x\left( {x - 1} \right)}} - \frac{{880\left( {x - 1} \right)}}{{x\left( {x - 1} \right)}} = \frac{{10x\left( {x - 1} \right)}}{{x\left( {x - 1} \right)}}\)
\(858x - 880\left( {x - 1} \right) = 10x\left( {x - 1} \right)\)
\(858x - 880x + 880 = 10{x^2} - 10x\)
\(10{x^2} + 12x - 880 = 0\)
\(5{x^2} + 6x - 440 = 0\)
Giải phương trình trên ta được: \({x_1} = - 10;\,\,{x_2} = 8,8.\)
Ta thấy chỉ có giá trị \({x_2} = 8,8\) thỏa mãn điều kiện.
Vậy khối lượng riêng của miếng kim loại thứ nhất là \(8,8\) g/cm3; khối lượng riêng của miếng kim loại thứ hai là \(8,8 - 1 = 7,8\) (g/cm3).
Lời giải
a) Thay \(x = - 1,y = 2\) vào hàm số, ta được: \(\left( {{m^2} - 1} \right).{\left( { - 1} \right)^2} = 2\) nên \({m^2} = 3\).
Suy ra \(m = \sqrt 3 \) hoặc \(m = - \sqrt 3 \).
Vậy đồ thị hàm số đi qua điểm \(A\left( { - 1;2} \right)\) là \(y = 2{x^2}\) khi \(m = \sqrt 3 \) hoặc \(m = - \sqrt 3 \).
b) Giải hệ phương trình \(\left\{ \begin{array}{l}3x + 2y = 3\\2x + y = 1\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = - 1\\y = 3\end{array} \right.\).
Do đó, đồ thị hàm số \(y = \left( {{m^2} - 1} \right){x^2}\) đi qua điểm có tọa độ \(\left( { - 1;3} \right)\).
Thay \(x = - 1,y = 3\) vào \(y = \left( {{m^2} - 1} \right){x^2}\), ta có: \(\left( {{m^2} - 1} \right).{\left( { - 1} \right)^2} = 3\) suy ra \({m^2} = 4\).
Suy ra \(m = 2\) hoặc \(m = - 2\).
Vậy đồ thị hàm số đi qua điểm có tọa độ \(\left( { - 1;3} \right)\) là \(y = 3{x^2}\) khi \(m = 2\) hoặc \(m = - 2\).
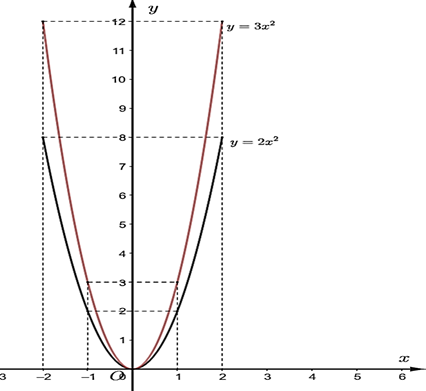
c) Ta có bảng giá trị của hàm số \(y = 2{x^2}\) như sau:
|
\(x\) |
\( - 2\) |
\( - 1\) |
\(0\) |
\(1\) |
\(2\) |
|
\(y\) |
\(8\) |
\(2\) |
\(0\) |
\(2\) |
\(8\) |
Vậy đồ thị hàm số \(y = 2{x^2}\) đi qua điểm có tọa độ \(\left( { - 2;8} \right);\left( { - 1;2} \right);\left( {0;0} \right);\left( {1;2} \right);\left( {2;8} \right)\).
Ta có bảng giá trị của hàm số \(y = 3{x^2}\) như sau:
|
\(x\) |
\( - 2\) |
\( - 1\) |
\(0\) |
\(1\) |
\(2\) |
|
\(y\) |
\(12\) |
\(3\) |
\(0\) |
\(3\) |
\(12\) |
Vậy đồ thị hàm số \(y = 3{x^2}\) đi qua điểm có tọa độ \(\left( { - 2;12} \right);\left( { - 1;3} \right);\left( {0;0} \right);\left( {1;3} \right);\left( {2;12} \right)\).
Từ đây, ta có đồ thị hàm số như sau:
Lời giải
a) Với \(m = \frac{1}{2}\), ta có: \({x^2} - \left( {2.\frac{1}{2} - 1} \right)x + {\left( {\frac{1}{2}} \right)^2} - 7 = 0\) suy ra \({x^2} - \frac{{27}}{4} = 0\) hay \({x^2} = \frac{{27}}{4}\).
Do đó, \(x = \frac{{3\sqrt 3 }}{2}\) hoặc \(x = \frac{{ - 3\sqrt 3 }}{2}\).
Vậy với \(m = \frac{1}{2}\) thì phương trình có nghiệm là \(\left\{ {\frac{{3\sqrt 3 }}{2};\frac{{ - 3\sqrt 3 }}{2}} \right\}\).
b) Xét phương trình \({x^2} - \left( {2m - 1} \right)x + {m^2} - 7 = 0\) có :
\(\Delta = {\left[ { - \left( {2m - 1} \right)} \right]^2} - 4\left( {{m^2} - 7} \right) = - 4m + 29\).
Để phương trình có nghiệm kép thì \(\Delta = 0\) hay \( - 4m + 29 = 0\), do đó \(m = \frac{{29}}{4}\).
Vậy phương trình có nghiệm kép khi \(m = \frac{{29}}{4}\).
c) Xét phương trình \({x^2} - \left( {2m - 1} \right)x + {m^2} - 7 = 0\) \(\left( * \right)\)
Ta có: \(\Delta = {\left( {2m - 1} \right)^2} - 4 \cdot 1 \cdot \left( {{m^2} - 7} \right) = 4{m^2} - 4m + 1 - 4{m^2} + 28 = - 4m + 29\).
Để phương trình \(\left( * \right)\) có hai nghiệm phân biệt \({x_1},{x_2}\) thì \(\Delta > 0,\) tức là \( - 4m + 29 > 0\) hay \(m < \frac{{29}}{4}.\)
Theo định lí Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m - 1\,\,\,\,\,\,\,\left( 1 \right)\\{x_1}{x_2} = {m^2} - 7\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Theo bài, \(4{x_1}^2 - {x_1} - 3x_2^2 + {x_2} = {x_1}{x_2}\)
\(4{x_1}^2 - 4x_2^2 - {x_1} + x_2^2 + {x_2} - {x_1}{x_2} = 0\)
\[4\left( {{x_1}^2 - x_2^2} \right) + {x_2}\left( {{x_2} - {x_1}} \right) + {x_2} - {x_1} = 0\]
\(4\left( {{x_1} - {x_2}} \right)\left( {{x_1} + {x_2}} \right) + \left( {{x_2} - {x_1}} \right)\left( {{x_2} + 1} \right) = 0\)
\(\left( {{x_1} - {x_2}} \right)\left( {4{x_1} + 4{x_2} - {x_2} - 1} \right) = 0\)
\(\left( {{x_1} - {x_2}} \right)\left( {4{x_1} + 3{x_2} - 1} \right) = 0\)
Xét trường hợp 1: \({x_1} - {x_2} = 0\) suy ra \({x_1} = {x_2}\) (loại do \({x_1} \ne {x_2}).\)
Xét trường hợp 2: \(4{x_1} + 3{x_2} - 1 = 0\) suy ra \({x_1} + 3\left( {{x_1} + {x_2}} \right) - 1 = 0\) \(\left( {**} \right)\)
Thay \({x_1} + {x_2} = 2m - 1\) vào \(\left( {**} \right)\) ta có: \({x_1} + 3\left( {2m - 1} \right) - 1 = 0\) hay \({x_1} = - 6m + 4\).
Thay \({x_1} = - 6m + 4\) vào \(\left( 1 \right)\) ta được \( - 6m + 4 + {x_2} = 2m - 1\), suy ra \({x_2} = 8m - 5.\)
Thay \({x_1} = - 6m + 4\) và \({x_2} = 8m - 5\) vào \(\left( 2 \right)\) ta được:
\(\left( { - 6m + 4} \right)\left( {8m - 5} \right) = {m^2} - 7\)
\( - 48{m^2} + 30m + 32m - 20 = {m^2} - 7\)
\( - 49{m^2} + 62m - 13 = 0\)
\(m = 1\) (thỏa mãn); \(m = \frac{{13}}{{49}}\) (thỏa mãn).
Vậy với \(m = \left\{ {1;\,\,\frac{{13}}{{49}}} \right\}\) thỏa mãn yêu cầu bài toán.
Lời giải
1. Gọi \[H\] là hình chiếu của \[A\] trên \[Oy.\] Ta có \(A\left( {2;\,\,3} \right)\) nên \(AH = \left| 2 \right| = 2\) và \[OH = \left| 3 \right| = 3.\]
Xét \[\Delta AOH\] vuông tại \[H,\] theo định lí Pythagore ta có:
\[O{A^2} = O{H^2} + A{H^2}\]
Suy ra \(OA = \sqrt {O{H^2} + A{H^2}} = \sqrt {{3^2} + {2^2}} = \sqrt {13} .\)
Ta cũng có \(\sin \widehat {AOH} = \frac{{AH}}{{OA}} = \frac{2}{{\sqrt {13} }}.\)
![1. Trong mặt phẳng tọa độ \(Oxy,\) cho điểm \(A\left( {2;\,\,3} \right).\) Thực hiện phép quay \(90^\circ \) ngược chiều kim đồng hồ quanh gốc tọa độ. Xác định tọa độ của điểm \(A\) sau khi quay. 2. Cho đường tròn tâm \(I\) nội tiếp tam giác \[ABC\] tiếp xúc với \[AB,{\rm{ }}AC\] lần lượt tại \[F\] và \[E.\] Kẻ \[CK\] vuông góc với \[BI.\] Chứng minh rằng: a) Tứ giác \(AEIF\) là tứ giác nội tiếp. b) \(\widehat {AIF} = \widehat {KIC}.\) c) Ba điểm \[F,{\rm{ }}E,{\rm{ }}K\] thẳng hàng. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/blobid8-1751336715.png)
Giả sử phép quay \(90^\circ \) ngược chiều kim đồng hồ quanh gốc tọa độ biến điểm \(A\) (ở góc phần tư thứ I) thành điểm \(B\). Khi đó, điểm \(B\) nằm ở góc phần tư thứ II và \(OB = OA = \sqrt {13} ,\,\,\widehat {AOB} = 90^\circ .\)
Ta có \(\widehat {AOB} = \widehat {AOH} + \widehat {BOH} = 90^\circ \) nên \(\cos \widehat {BOH} = \sin \widehat {AOH} = \frac{2}{{\sqrt {13} }}.\)
Xét \(\Delta OBK\) vuông tại \(K\) (gọi \(K\) là hình chiếu của điểm \(B\) trên \(Oy)\) ta có:
\(OK = OB \cdot \cos \widehat {BOH} = \sqrt {13} \cdot \frac{2}{{\sqrt {13} }} = 2.\)
Từ đó, ta có tung độ của điểm \(B\) là \(2\) (do \(B\) nằm ở góc phần tư thứ II).
Tương tự, ta tìm được hoành độ của điểm \(B\) là \( - 3.\)\(\)
Như vậy, phép quay ngược chiều \[90^\circ \] tâm \[O\] biến điểm \(A\left( {2;\,\,3} \right)\) thành điểm \[B\left( {--3;{\rm{ }}2} \right).\]
2.
![1. Trong mặt phẳng tọa độ \(Oxy,\) cho điểm \(A\left( {2;\,\,3} \right).\) Thực hiện phép quay \(90^\circ \) ngược chiều kim đồng hồ quanh gốc tọa độ. Xác định tọa độ của điểm \(A\) sau khi quay. 2. Cho đường tròn tâm \(I\) nội tiếp tam giác \[ABC\] tiếp xúc với \[AB,{\rm{ }}AC\] lần lượt tại \[F\] và \[E.\] Kẻ \[CK\] vuông góc với \[BI.\] Chứng minh rằng: a) Tứ giác \(AEIF\) là tứ giác nội tiếp. b) \(\widehat {AIF} = \widehat {KIC}.\) c) Ba điểm \[F,{\rm{ }}E,{\rm{ }}K\] thẳng hàng. (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/07/blobid9-1751336724.png)
a) Vì \(F,\,\,E\) là tiếp điểm của đường tròn \(\left( I \right)\) nội tiếp tam giác \(ABC\), do đó \[IF \bot AB,\,\,IE \bot AC.\]
Do đó \(\widehat {IFA} = \widehat {IEA} = 90^\circ \), nên hai tam giác \(AIF,\,\,AIE\) là hai tam giác vuông có cùng cạnh huyền \(AI\)
Do đó đường tròn ngoại tiếp hai tam giác \(AIF,\,\,AIE\) là đường tròn đường kính \(AI\) hay bốn điểm \(A,\,\,E,\,\,I,\,\,F\) cùng nằm trên đường tròn đường kính \(AI.\)
Vậy tứ giác \(AEIF\) là tứ giác nội tiếp.
b) Đường tròn tâm \(I\) nội tiếp tam giác \(ABC\) nên \(AI,\,\,BI,\,\,CI\) là các đường phân giác của tam giác.
Do đó \(\widehat {IAF} = \frac{1}{2}\widehat {BAC};\,\,\widehat {IBC} = \frac{1}{2}\widehat {ABC};\,\,\widehat {ICB} = \frac{1}{2}\widehat {ACB}\).
Ta có: \(\widehat {AIF} = 90^\circ - \widehat {IAF} = 90^\circ - \frac{1}{2}\widehat {BAC}\). (1)
\[\widehat {IBC} + \widehat {ICB} = \frac{1}{2}\widehat {ABC} + \frac{1}{2}\widehat {ACB} = \frac{1}{2}\left( {\widehat {ABC} + \widehat {ACB}} \right) = \frac{1}{2}\left( {180^\circ - \widehat {BAC}} \right) = 90^\circ - \frac{1}{2}\widehat {BAC}.\] (2)
Xét \(\Delta IBC\) có \(\widehat {KIC}\) là góc ngoài tại đỉnh \(I\) nên \(\widehat {KIC} = \widehat {IBC} + \widehat {ICB}.\) (3)
Từ (1), (2) và (3) suy ra \(\widehat {AIF} = \widehat {KIC}.\) (4)
c) Tứ giác \(AEIF\) là tứ giác nội tiếp nên \(\widehat {AEF} = \widehat {AIF}\) (hai góc nội tiếp cùng chắn cung \(AF).\) (5)
Chứng minh tương tự câu 1, ta có tứ giác \(IEKC\) nội tiếp đường tròn đường kính \(IC.\)
Do đó \(\widehat {KEC} = \widehat {KIC}\) (hai góc nội tiếp cùng chắn cung \(KC).\) (6)
Từ (4), (5), (6) ta có \(\widehat {AEF} = \widehat {KEC}\).
Mà \(\widehat {AEF} + \widehat {FEC} = 180^\circ \) nên \(\widehat {KEC} + \widehat {FEC} = 180^\circ \) hay ba điểm \(F,\,\,E,\,\,K\) thẳng hàng.
Lời giải
Điều kiện \(x \ge 1\).
Ta có: \({x^2} - 29x + 28 = 4\sqrt {x - 1} \)
\({x^2} - 10x + 25 + x - 1 - 4\sqrt {x - 1} + 4 = 0\)
\({\left( {x - 5} \right)^2} + {\left( {\sqrt {x - 1} - 2} \right)^2} = 0\)
Nhận thấy \({\left( {x - 5} \right)^2} \ge 0\), \({\left( {\sqrt {x - 1} - 2} \right)^2} \ge 0\) với mọi \(x \ge 1\).
Do đó, \({\left( {x - 5} \right)^2} + {\left( {\sqrt {x - 1} - 2} \right)^2} \ge 0\).
Suy ra để \({\left( {x - 5} \right)^2} + {\left( {\sqrt {x - 1} - 2} \right)^2} = 0\) thì đồng thời \({\left( {x - 5} \right)^2} = 0\) và \({\left( {\sqrt {x - 1} - 2} \right)^2} = 0\).
Suy ra \(\left\{ \begin{array}{l}{\left( {x - 5} \right)^2} = 0\\{\left( {\sqrt {x - 1} - 2} \right)^2} = 0\end{array} \right.\) nên \(\left\{ \begin{array}{l}x = 5\\\sqrt {x - 1} = 2\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 5\\x - 1 = 4\end{array} \right.\).
Do đó, \(x = 5\) (thỏa mãn).