Đề thi cuối học kỳ 2 Toán 9 Kết nối tri thức có đáp án - Đề 1
116 người thi tuần này 4.6 468 lượt thi 11 câu hỏi 60 phút
🔥 Đề thi HOT:
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
25.1 K lượt thi
3 câu hỏi
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
20.1 K lượt thi
20 câu hỏi
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
6.6 K lượt thi
5 câu hỏi
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
1.9 K lượt thi
16 câu hỏi
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
21.9 K lượt thi
4 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
3.7 K lượt thi
20 câu hỏi
123 bài tập Nón trụ cầu và hình khối có lời giải
1.4 K lượt thi
123 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Đoạn văn 1
Câu 1-2. (2,5 điểm)
Lời giải
1. Xét đồ thị hàm số \(y = 5{x^2}\).
a) Với \(x = - 2\) thì \(y = 5 \cdot {\left( { - 2} \right)^2} = 20.\)
Vậy tọa độ điểm cần tìm là \(\left( { - 2\,;\,\,20} \right).\)
b) Với \(x = 5\) thì \(5{x^2} = 5\) nên \({x^2} = 1.\)
Do đó \(x = 1\) hoặc \(x = - 1.\)
Vậy có hai điểm thỏa mãn yêu cầu bài toán là \(\left( {1\,;\,\,5} \right)\) hoặc \(\left( { - 1\,;\,\,5} \right).\)
Lời giải
2. Gọi \(x\,\,\left( {\rm{\% }} \right)\) là lãi suất trong một năm của ngân hàng \(\left( {x > 0} \right)\).
Sau năm thứ nhất người đó phải trả:
\(20\,\,000\,\,000 + 20\,\,000\,\,000 \cdot \frac{x}{{100}} = 200\,\,000\left( {100 + x} \right)\)
Số tiền sau năm thứ hai tăng thêm là:
\(200\,\,000\left( {100 + x} \right)\frac{x}{{100}} = 2\,\,000x\left( {x + 100} \right)\)
Theo bài ra, ta có phương trình:
\(200\,\,000\left( {100 + x} \right) + 2\,\,000x\left( {x + 100} \right) = 24\,\,200\,\,000\)
\(100\left( {100 + x} \right) + x\left( {x + 100} \right) = 12\,\,100\)
\({x^2} + 200x - 2\,\,100\,\,000 = 0\)
\(x = 10\) (TMĐK) hoặc \(x = - 210\) (loại).
Vậy lãi của ngân hàng một năm là \(10{\rm{\% }}\).
Lời giải
a) Tần số tương đối của các nhóm lần lượt là:
\[{f_1} = \frac{{20}}{{100}} \cdot 100\% = 20\% \]; \[{f_2} = \frac{{15}}{{100}} \cdot 100\% = 15\% \];
\[{f_3} = \frac{{25}}{{100}} \cdot 100\% = 25\% \];\[{f_4} = \frac{{30}}{{100}} \cdot 100\% = 30\% \]; \[{f_5} = \frac{{10}}{{100}} \cdot 100\% = 10\% \].
b) Bảng tần số tương đối của mỗi nhóm
|
Nhóm |
\[\left[ {36\,;\,38} \right)\] |
\[\left[ {38\,;40} \right)\] |
\[\left[ {40\,;42} \right)\] |
\[\left[ {42\,;\,44} \right)\] |
\[\left[ {44\,;46} \right)\] |
|
Tần số tương đối \[\left( n \right)\] |
\[20\] |
\[15\] |
\[25\] |
\[30\] |
\[10\] |
Biểu đồ cột của mẫu số liệu ghép nhóm:
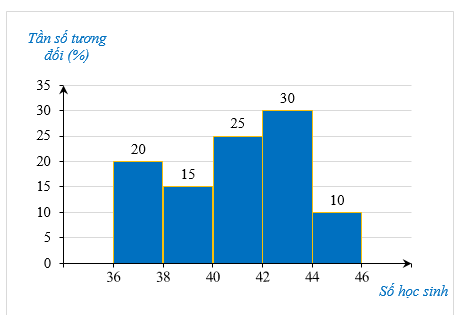
Lời giải
|
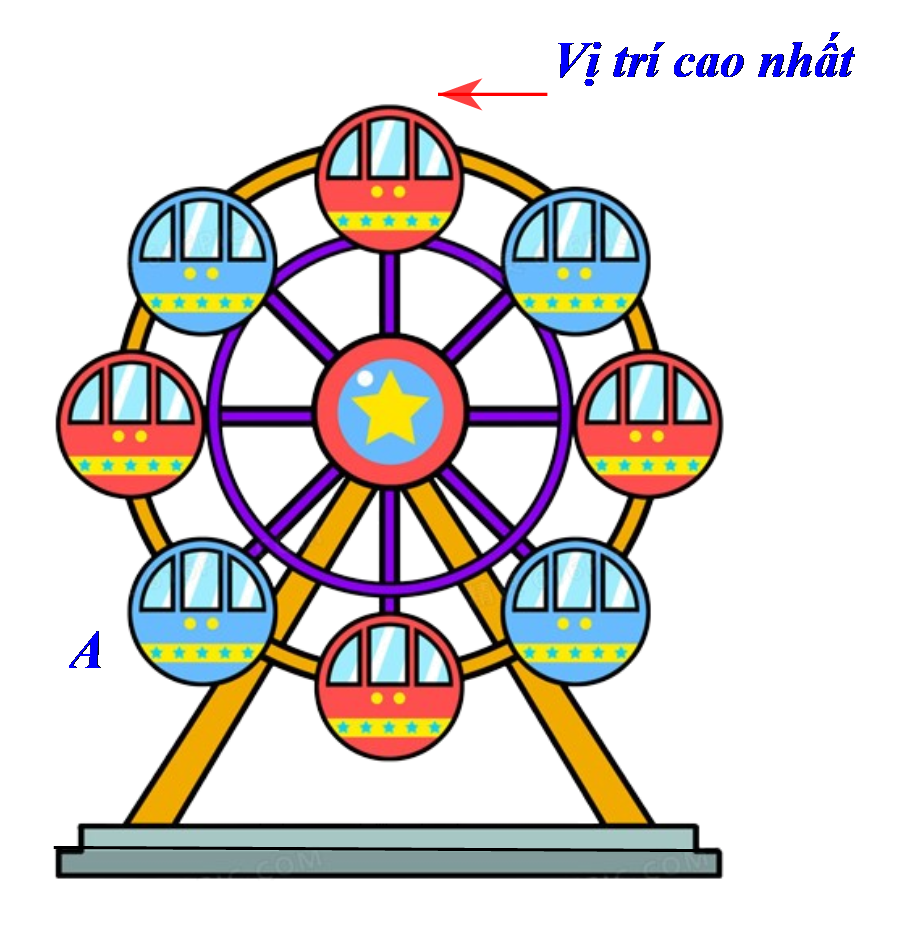
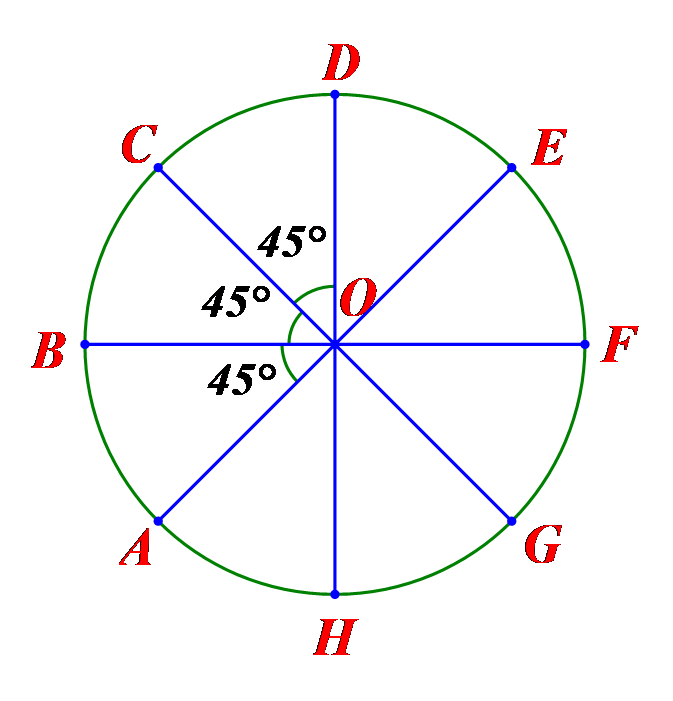
Ta có một bát giác đều \(ABCDEFGH\) nội tiếp trong đường tròn \(\left( O \right)\), mỗi góc ở tâm là: \(360^\circ :8 = 45^\circ .\) Theo giả thiết, ta có: \(\widehat {AOD} = 3 \cdot 45^\circ = 135^\circ .\;\) Vậy qua phép quay thuận chiểu \(135^\circ \) tâm \(O\), cabin \(A\) di chuyển đến vị trí cao nhất (điểm \(D).\) |
 |
Đoạn văn 2
Câu 4-5. (1,5 điểm) Hộp thứ nhất đựng 1 quả bóng trắng, 1 quả bóng đó. Hộp thứ 2 đựng 1 quả bóng đó, 1 quả bóng vàng. Lấy ra ngẫu nhiên từ mỗi hộp 1 quả bóng.
Lời giải
a) Kí hiểu \[T\] là màu trắng, là màu đỏ và \[V\] là màu vàng.
Không gian mẫu .
Do đó, không gian mẫu có 4 phần tử.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Câu 7-9. (2,5 điểm)
Cho đường tròn \(\left( {O;\,\,R} \right)\). Từ \(A\) trên \(\left( O \right),\) kẻ tiếp tuyến \(d\) với \(\left( O \right).\) Trên đường thẳng \(d\) lấy điểm \(M\) bất kỳ \(\left( M \right.\) khác \(\left. A \right),\) kẻ cát tuyến \(MNP.\) Gọi \(K\) là trung điểm của \(NP,\) kẻ tiếp tuyến \(MB.\) Kẻ \[AC \bot MB,\,\,BD \bot AM\,\,\left( {C \in MB,\,\,D \in AM} \right).\] Gọi\[H\] là giao điểm của \[AC\] và \[BD,\] \[I\] là giao điểm của \[OM\] và \[AB.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Câu 10-11. (1,5 điểm) Một hộp đựng bóng tennis có dạng hình trụ chứa vừa khít ba quả bóng tennis xếp theo chiều dọc (hình vẽ). Các quả bóng tennis có dạng hình cầu, đường kính \(6,4\;{\rm{cm}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
4.6
94 Đánh giá
50%
40%
0%
0%
0%