Bộ 5 đề thi giữa kì 1 Toán 11 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 3
29 người thi tuần này 4.6 535 lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 8 (có lời giải) - Đề 1
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 3
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 2
Đề kiểm tra Góc giữa đường thẳng và mặt phẳng góc nhị diện (có lời giải) - Đề 1
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 3
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 2
Đề kiểm tra Khoảng cách trong không gian (có lời giải)- Đề 1
Đề kiểm tra Hai mặt phẳng vuông góc (có lời giải) - Đề 3
Danh sách câu hỏi:
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Ta có: \[\sin x = \frac{4}{5}\] với \[\frac{\pi }{2} < x < \pi \] thì \[x\] thuộc góc phần tư thứ II.
Do đó, \[\cos x < 0\].
Vậy \[\cos x = - \sqrt {1 - {{\sin }^2}x} = - \frac{3}{5}\].
Câu 3
Xác định số đo của góc lượng giác \[\left( {Ou,Ov} \right)\] được biểu diễn trong hình bên dưới đây.
![Xác định số đo của góc lượng giác \[\left( {Ou,Ov} \right)\] được biểu diễn trong hình bên dưới đây. A. \[ - 300^\circ .\] B. \[510^\circ .\] C. \[60^\circ .\] D. \[ - 420^\circ .\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/17-1760799467.png)
Xác định số đo của góc lượng giác \[\left( {Ou,Ov} \right)\] được biểu diễn trong hình bên dưới đây.
![Xác định số đo của góc lượng giác \[\left( {Ou,Ov} \right)\] được biểu diễn trong hình bên dưới đây. A. \[ - 300^\circ .\] B. \[510^\circ .\] C. \[60^\circ .\] D. \[ - 420^\circ .\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/17-1760799467.png)
A. \[ - 300^\circ .\]
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Ta có: \[\left( {Ou,Ov} \right) = - \left( {360^\circ - 60^\circ } \right) = - 300^\circ \].
Câu 4
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Điều kiện: \[1 - \cos x \ne 0\] \[ \Leftrightarrow \cos x \ne 1\]\[ \Leftrightarrow x \ne k2\pi ,{\rm{ }}k \in \mathbb{Z}.\]
Vậy tập xác định của hàm số \[y = \frac{{\sin x}}{{1 - \cos x}}\] là \[D = \mathbb{R}\backslash \left\{ {k2\pi |k \in \mathbb{Z}} \right\}.\]
Câu 5
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Ta có: \[2\sin x - \sqrt 3 = 0\]
\[ \Leftrightarrow \sin x = \frac{{\sqrt 3 }}{2}\] \[ \Leftrightarrow \sin x = \sin \left( {\frac{\pi }{3}} \right)\] \[ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \frac{{2\pi }}{3} + k2\pi \end{array} \right.,{\rm{ }}k \in \mathbb{Z}.\]
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
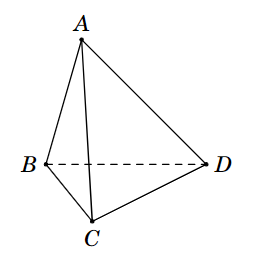
Cho hình chóp \[S.ABCD\], biết \[AB\] cắt \[CD\] tại \[E\], \[AC\] cắt \[BD\] tại \[F\] trong mặt phẳng đáy. Xét tính đúng sai của các khẳng định sau:
a) Đường thẳng \[FE\] nằm trong mặt phẳng \[\left( {ABCD} \right).\]
b) \[AB\] là giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {ABCD} \right).\]
c) \[SF\] là giao điểm của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\], \[SE\] là giao tuyến của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SBD} \right).\]
d) Gọi \[G = FE \cap AD\]. Khi đó, \[SG\] là giao tuyến của mặt phẳng \[\left( {SFE} \right)\] và mặt phẳng \[\left( {SAD} \right)\].
Cho hình chóp \[S.ABCD\], biết \[AB\] cắt \[CD\] tại \[E\], \[AC\] cắt \[BD\] tại \[F\] trong mặt phẳng đáy. Xét tính đúng sai của các khẳng định sau:
a) Đường thẳng \[FE\] nằm trong mặt phẳng \[\left( {ABCD} \right).\]
b) \[AB\] là giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {ABCD} \right).\]
c) \[SF\] là giao điểm của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\], \[SE\] là giao tuyến của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SBD} \right).\]
d) Gọi \[G = FE \cap AD\]. Khi đó, \[SG\] là giao tuyến của mặt phẳng \[\left( {SFE} \right)\] và mặt phẳng \[\left( {SAD} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Một cây cầu có dạng cung \[OA\] là một phần của đ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/23-1760800085.png)