Đề kiểm tra Đường tiệm cận của đồ thị hàm số (có lời giải) - Đề 3
44 người thi tuần này 4.6 1 K lượt thi 24 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Câu 1
Lời giải
Tập xác định \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).
Ta có: \(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{{x - 2}}{{x + 1}} = - \infty .\)
\(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} \frac{{x - 2}}{{x + 1}} = + \infty .\)
Vậy đường thẳng \(x = - 1\)là tiệm cận đứng của đồ thị hàm số đã cho.
Vậy chọn đáp án A.
Câu 2
Lời giải
Tập xác định \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).
Ta có: \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{{2x + 3}}{{x - 1}} = \mathop {\lim }\limits_{x \to - \infty } \left( {2 + \frac{5}{{x - 1}}} \right) = 2,\)
\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 3}}{{x - 1}} = \mathop {\lim }\limits_{x \to + \infty } \left( {2 + \frac{5}{{x - 1}}} \right) = 2.\)
Vậy đường thẳng \(y = 2\)là tiệm cận ngang của đồ thị hàm số đã cho.
Vậy chọn đáp án B.
Câu 3
Lời giải
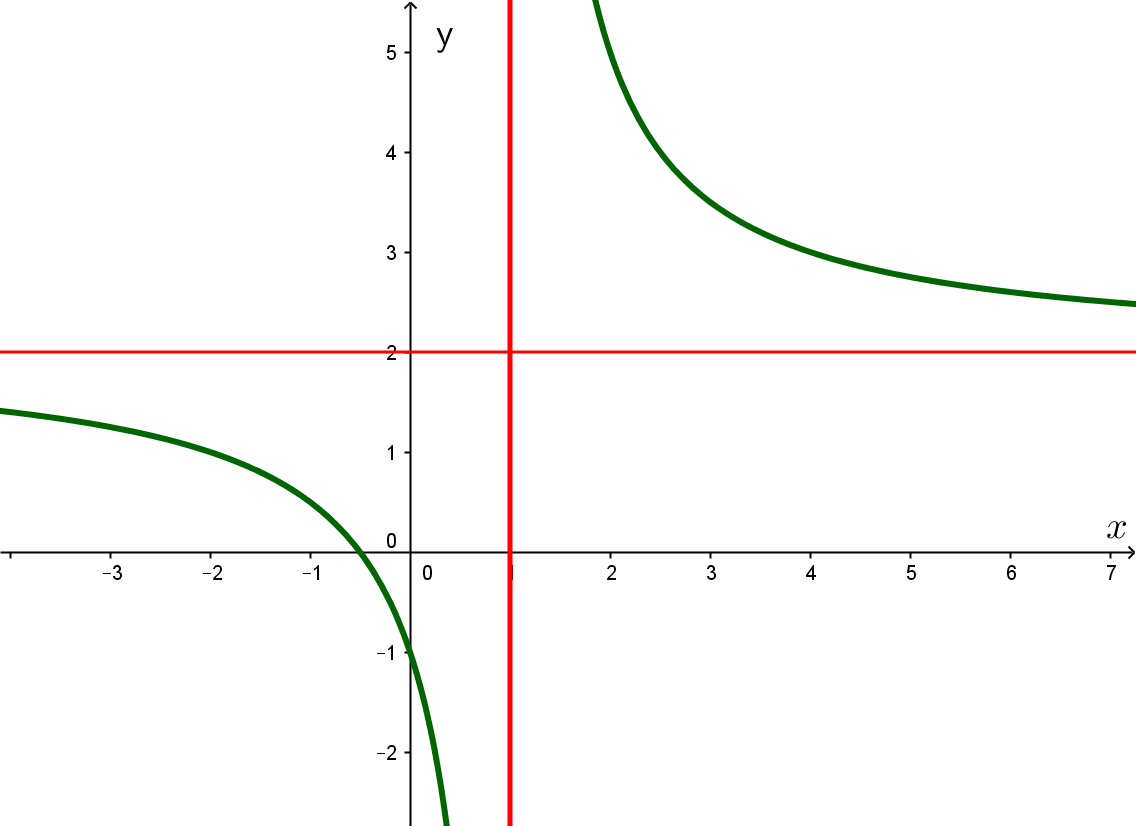
Từ đồ thị hàm số ta có:
+) Tập xác định \(D = \mathbb{R}\) nên đáp án A, C bị loại.
+) Tiệm cận ngang \(y = 2\)nên đáp án B bị loại.
Vì: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {e^x} = + \infty .\\\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } {e^x} = 0.\end{array} \right. \Rightarrow y = 0\)là TCN của đồ thị hàm số \(y = {e^x}\).
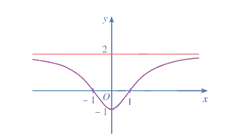
+) Đồ thị hàm số \(y = \frac{{2{x^2} - 2}}{{{x^2} + 2}}\) có đường tiệm cận ngang \(y = 2\)vì
\(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 2}}{{{x^2} + 2}} = \mathop {\lim }\limits_{x \to + \infty } \left( {2 - \frac{6}{{{x^2} + 2}}} \right) = 2.\\\mathop {\lim }\limits_{x \to - \infty } \frac{{2{x^2} - 2}}{{{x^2} + 2}} = \mathop {\lim }\limits_{x \to - \infty } \left( {2 - \frac{6}{{{x^2} + 2}}} \right) = 2.\end{array}\)
Vậy chọn đáp án D.
Câu 4
Lời giải
Từ đồ thị hàm số ta có:
+) Tập xác định \(D = \mathbb{R}\) nên đáp án A, B, D bị loại.
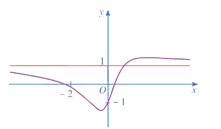
+) Đồ thị hàm số \(y = \frac{{{x^2} + 2x - 1}}{{{x^2} + 1}}\) có đường tiệm cận ngang \(y = 1\) vì
\(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} + 2x - 1}}{{{x^2} + 1}} = \mathop {\lim }\limits_{x \to + \infty } \left( {1 + \frac{{2x - 2}}{{{x^2} + 1}}} \right) = 1.\\\mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + 2x - 1}}{{{x^2} + 1}} = \mathop {\lim }\limits_{x \to - \infty } \left( {1 + \frac{{2x - 2}}{{{x^2} + 1}}} \right) = 1.\end{array}\)
Câu 5
Lời giải
Tập xác định \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).
Ta có \(\mathop {\lim }\limits_{x \to \pm \infty } y = - 5 \Rightarrow y = - 5\) là tiệm cận ngang của đồ thị hàm số đã cho.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
Cho đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - \left( {2m + 1} \right)x + {m^2} - 3}}\] với tham số \[m\]. Xét tính đúng – sai của các phát biểu sau:
a) Với mọi \(m\) đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - \left( {2m + 1} \right)x + {m^2} - 3}}\] không tiệm cận đứng và tiệm cận ngang.
b) Đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - \left( {2m + 1} \right)x + {m^2} - 3}}\] có 1 tiệm cận ngang là \[y = 0\].
c) Với \(m = - 1\) thì đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - \left( {2m + 1} \right)x + {m^2} - 3}}\] có \(2\) đường tiệm cận đứng.
d) Có ba giá trị của \(m\) đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - \left( {2m + 1} \right)x + {m^2} - 3}}\] có đúng hai đường tiệm cận.
Cho đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - \left( {2m + 1} \right)x + {m^2} - 3}}\] với tham số \[m\]. Xét tính đúng – sai của các phát biểu sau:
a) Với mọi \(m\) đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - \left( {2m + 1} \right)x + {m^2} - 3}}\] không tiệm cận đứng và tiệm cận ngang.
b) Đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - \left( {2m + 1} \right)x + {m^2} - 3}}\] có 1 tiệm cận ngang là \[y = 0\].
c) Với \(m = - 1\) thì đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - \left( {2m + 1} \right)x + {m^2} - 3}}\] có \(2\) đường tiệm cận đứng.
d) Có ba giá trị của \(m\) đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - \left( {2m + 1} \right)x + {m^2} - 3}}\] có đúng hai đường tiệm cận.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
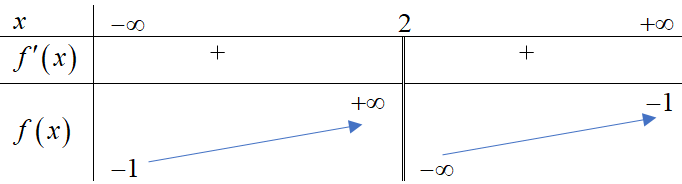
![Câu 18: Cho hàm số bậc ba \[y = f\left( x \right)\] có đạo hàm liên tục trên \[\mathbb{R}\]. Đồ thị hàm \[y = f\left( x \ri (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/9-1759194921.png)
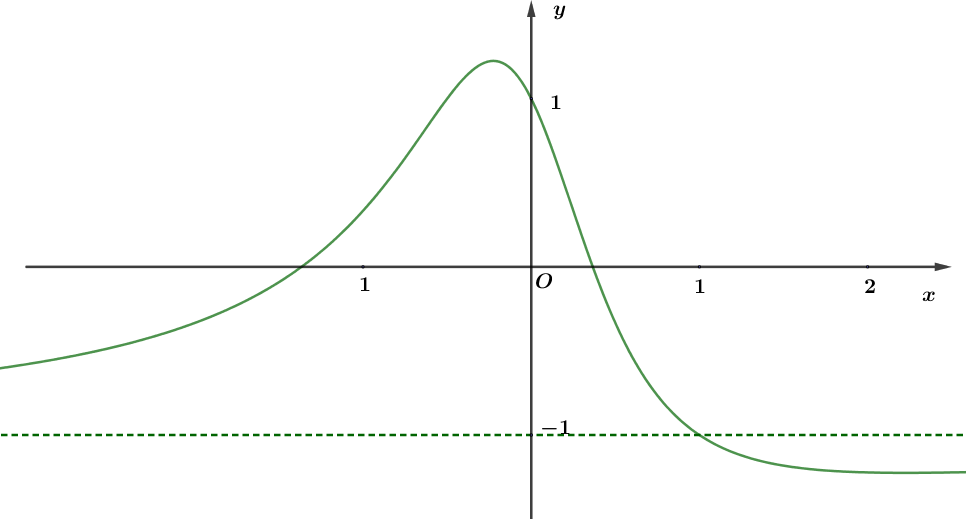
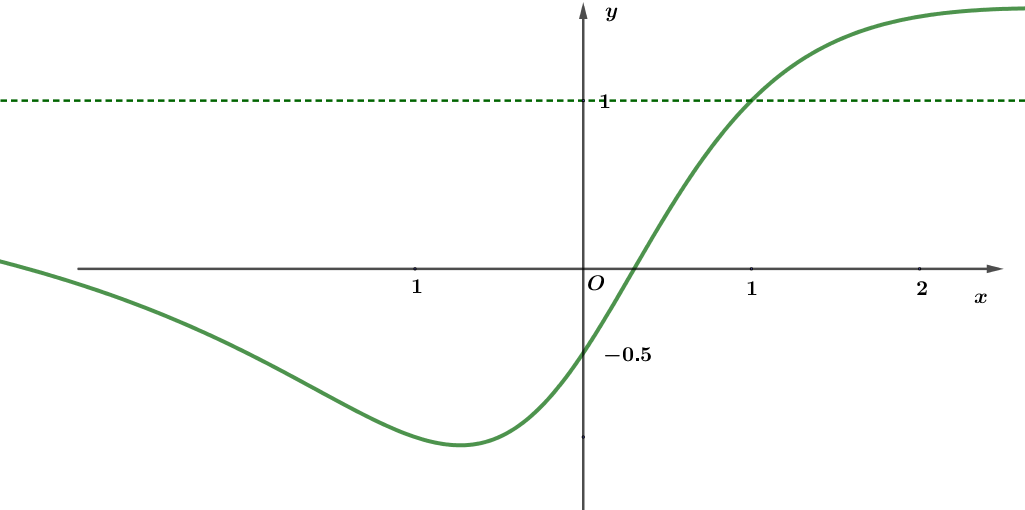
![Đồ thị hàm số \[y = \left| {f\left( x \right)} \right|\] có 2 tiệm cận ngang là hai đường thẳng \[y = m\] và \[y = n\]. Tính \(m + n\)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/12-1759195052.png)
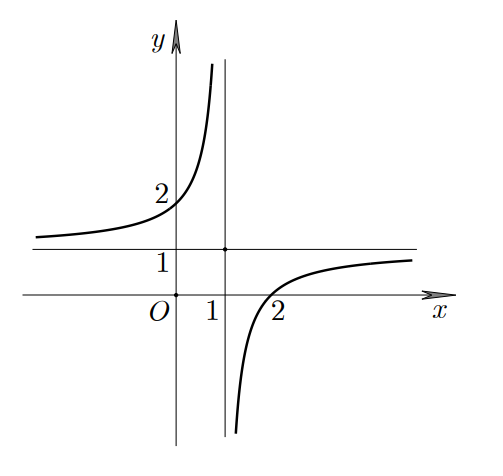
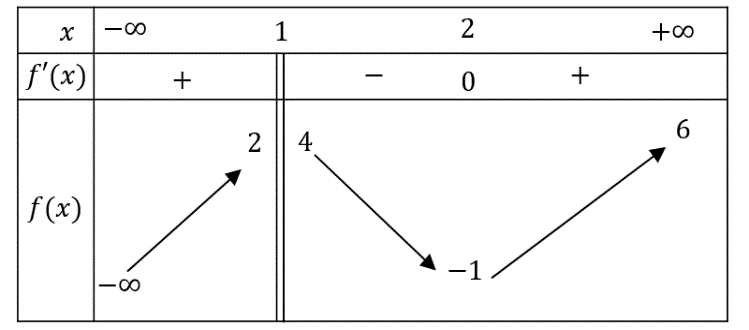
![Câu 22: Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau: Đồ thị hàm số\[g\left( x \right){\rm{ }} = \frac{2}{{3f\left( x \right) - 2}}\] có tất cả bao nhiêu đường tiệm cận? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/14-1759195115.png)
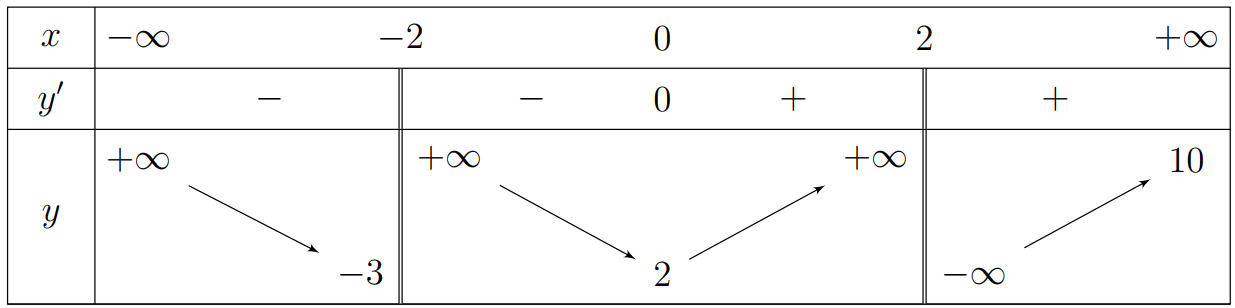
![Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \[y = \frac{2}{{3f(x) - 2}}\]là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/15-1759195174.png)