Đề kiểm tra Ôn tập cuối chương 2 (có lời giải) - Đề 3
41 người thi tuần này 4.6 1.5 K lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Câu 1
Lời giải
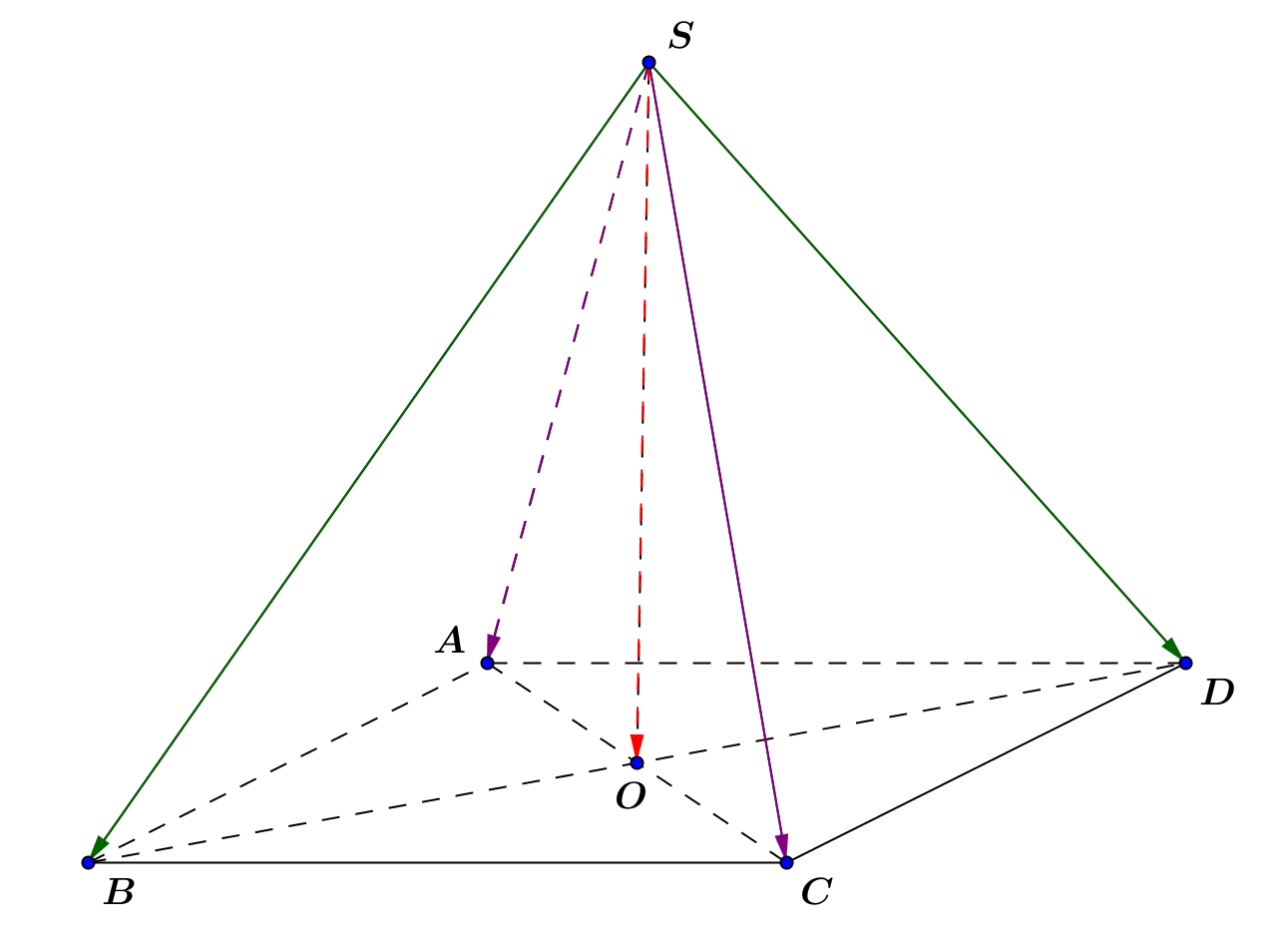
Với \[O\] là trung điểm của \[AC\], ta có \[\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} \].
Với \[O\] là trung điểm của \[BD\], ta có \[\overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} \].
Từ đó suy ra \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \) và \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \).
\[\overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow {BA} + \overrightarrow {AC} + \overrightarrow {DC} + \overrightarrow {CA} = \overrightarrow {BA} + \overrightarrow {DC} + \left( {\overrightarrow {AC} + \overrightarrow {CA} } \right) = \overrightarrow {BA} + \overrightarrow {DC} \].
\(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AC} + \overrightarrow {CB} + \overrightarrow {CB} + \overrightarrow {BD} = \overrightarrow {AC} + \overrightarrow {BD} + 2\overrightarrow {CB} \).
Câu 2
Lời giải
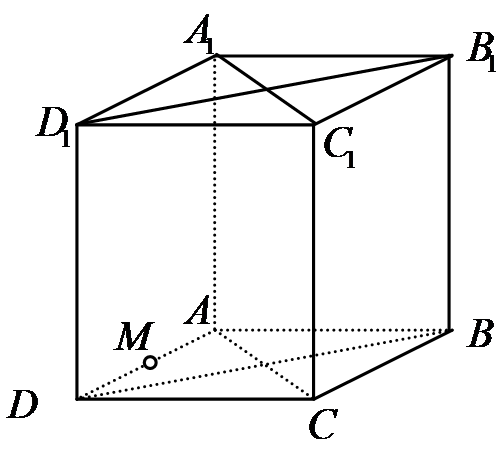
Ta có: \[\overrightarrow {{B_1}M} .\overrightarrow {B{D_1}} = \left( {\overrightarrow {{B_1}B} + \overrightarrow {BA} + \overrightarrow {AM} } \right)\left( {\overrightarrow {BA} + \overrightarrow {AD} + \overrightarrow {D{D_1}} } \right)\]
\[\begin{array}{l} = \overrightarrow {{B_1}B} .\overrightarrow {D{D_1}} + {\overrightarrow {BA} ^2} + \overrightarrow {AM} .\overrightarrow {AD} \\ = - {a^2} + {a^2} + \frac{{{a^2}}}{2}\\ = \frac{{{a^2}}}{2}\end{array}\]
Câu 3
Lời giải
Câu 4
Lời giải
Áp dụng định lí: trong không gian với hệ tọa độ \[Oxyz\], cho hai điểm \(A\left( {{x_A};{y_A};{z_A}} \right)\) và \(B\left( {{x_B};{y_B};{z_B}} \right)\). Khi đó, ta có: \[\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\].
Ta có: \[\overrightarrow {MN} = \left( {\frac{1}{2} - \frac{1}{2};\left( { - 2} \right) - 1;4 - \left( { - 3} \right)} \right) = \left( {0; - 3;7} \right)\].
Câu 5
Lời giải
Ta có \[\overrightarrow {AB} = \left( {4;x - 5;2} \right),\,\,\overrightarrow {AC} = \left( {6; - 3;y + 1} \right)\]
\(A,\,\,B,\,\,C\)thẳng hàng khi \[\overrightarrow {AB} ,\,\,\overrightarrow {AC} \] cùng phương \[ \Leftrightarrow \frac{4}{6} = \frac{{x - 5}}{{ - 3}} = \frac{2}{{y + 1}} \Leftrightarrow \left\{ \begin{array}{l}6\left( {x - 5} \right) = - 12\\4\left( {y + 1} \right) = 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 2\end{array} \right.\]
Vậy \(x + y = 5.\)
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.