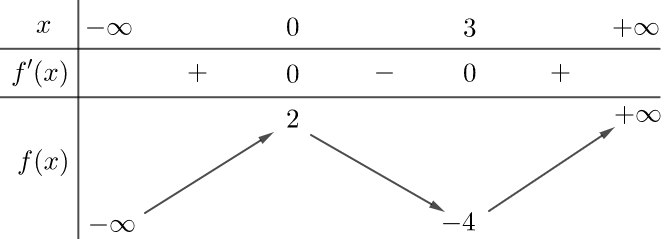
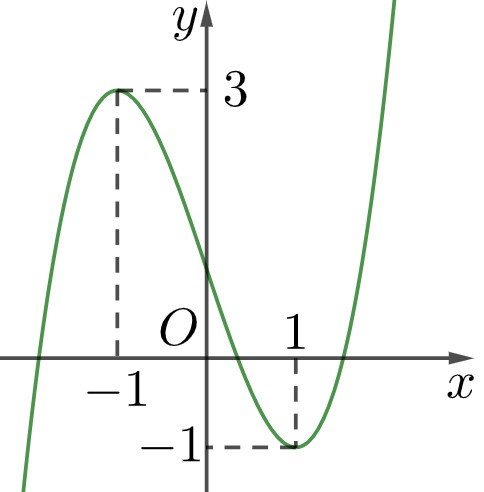
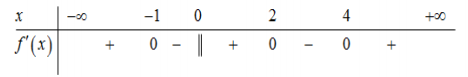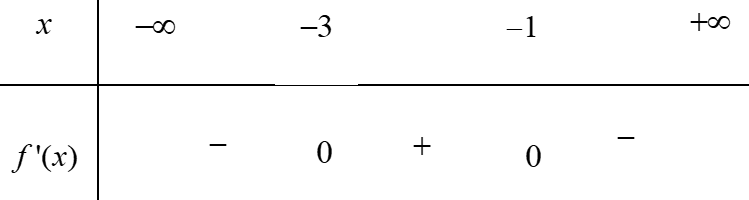Đề kiểm tra Tính đơn điệu và cực trị của hàm số (có lời giải) - Đề 4
56 người thi tuần này 4.6 800 lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
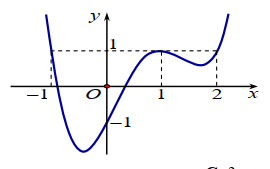
Câu 1
Lời giải
Tập xác định: \(D = \mathbb{R}\).
Ta có \(y' = 3{x^2} + 3 > 0\), \(\forall x \in \mathbb{R}\) suy ra hàm số đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\).
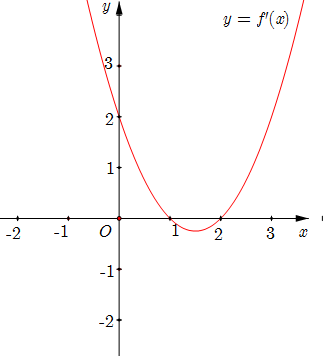
Câu 2
Lời giải
Tập xác định \[D = \mathbb{R}\].
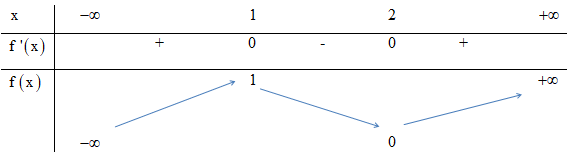
Tính \[y' = {x^2} - 4x + 3\].
Cho \[y' = 0 \Leftrightarrow {x^2} - 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\].
Bảng biến thiên
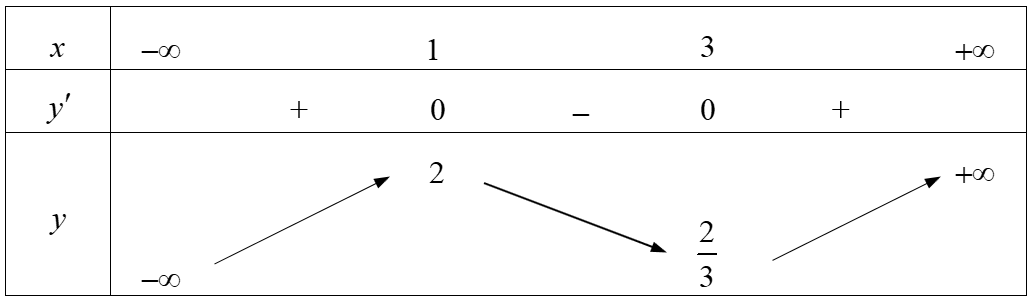
Vậy điểm cực đại của đồ thị hàm số là \[\left( {1;2} \right).\]
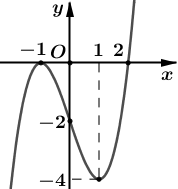
Câu 3
Lời giải
Tập xác định \[D = \mathbb{R}\].
Có \(y' = 3{x^2} + 6x - 9\) nên \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\).
![Biết đồ thị hàm số \(y = {x^3} + 3{x^2} - 9x - 1\) có hai cực trị \[A\] và \[B\]. Điểm nào dưới đây thuộc đường thẳng\[AB\]? A. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/1-1759133809.png)
Vậy hai điểm cực trị của đồ thị hàm số trên là \(A\left( {1; - 6} \right)\), \(B\left( { - 3;26} \right)\).
Phương trình đường thẳng qua \[A\] và \[B\] là \[\Delta :y = - 8x + 2\].
Ta thấy đường thẳng \[\Delta \] qua \[N\left( {0;\,2} \right)\].
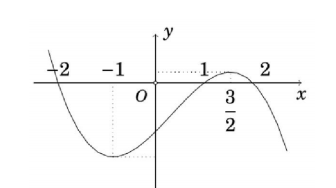
Câu 4
Lời giải
TXĐ: \(D = \mathbb{R}\).
Có \(y = \sqrt {{x^2} + 1} - mx - 1 \Rightarrow y' = \frac{x}{{\sqrt {{x^2} + 1} }} - m\).
Theo yêu cầu bài toán: \(y' = \frac{x}{{\sqrt {{x^2} + 1} }} - m \ge 0{\rm{, }}\forall x \in \mathbb{R}\)\( \Leftrightarrow m \le \frac{x}{{\sqrt {{x^2} + 1} }},{\rm{ }}\forall x \in \mathbb{R}{\rm{ }}\left( 1 \right)\).
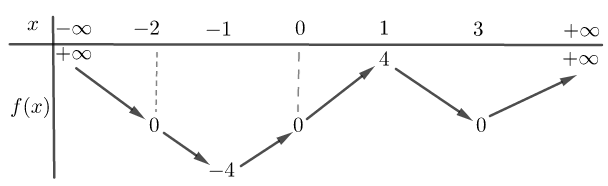
Xét hàm số \(g\left( x \right) = \frac{x}{{\sqrt {{x^2} + 1} }}\) với \[x \in \mathbb{R}\]. Ta có \(g'\left( x \right) = \frac{1}{{\sqrt {{x^2} + 1} \left( {{x^2} + 1} \right)}} > 0,{\rm{ }}\forall x \in \mathbb{R}\).
Bảng biến thiên
![Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 2024;2024} \right]\) để hàm số \(y = \sqrt {{x^2} + 1} - mx - 1\) đồng biến trên \(\mathbb{R}\). A. \(2024\). B. \(2019\). C. \(2020\). D. \(0\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/2-1759133862.png)
Từ \(\left( 1 \right) \Rightarrow m \le - 1\) mà \(\left\{ \begin{array}{l}m \in \left[ { - 2024;2024} \right]\\m \in \mathbb{Z}\end{array} \right.\) nên có 2024 giá trị nguyên.
Câu 5
Lời giải
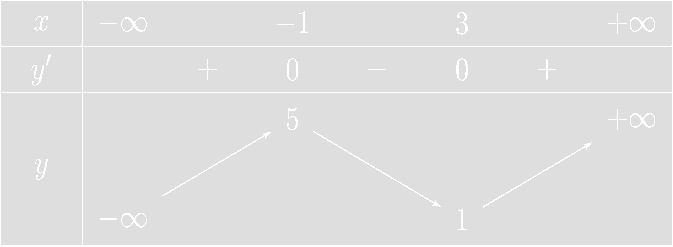
Căn cứ BBT ta thấy hàm số đồng biến trên \[(2; + \infty )\]
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.