Đề thi tuyển sinh vào lớp 10 Toán năm học 2016 - 2017 Sở GD&ĐT Đà Nẵng có đáp án
49 người thi tuần này 4.6 149 lượt thi 7 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
Lời giải
Ta có: \[M = \frac{{{{\left( {a + b} \right)}^2} - {{\left( {a - b} \right)}^2}}}{{ab}}\]\[ = \frac{{\left( {a + b + a - b} \right)\left( {a + b - a + b} \right)}}{{ab}} = \frac{{2a.2b}}{{ab}} = 4\].
Lời giải
\[\left\{ \begin{array}{l}2x - y = 0\\3x - 2y = 1\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}4x - 2y = 0\\3x - 2y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\3.\left( { - 1} \right) - 2y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = - 2\end{array} \right.\].
Vậy hệ có nghiệm duy nhất (–1;–2).
Lời giải
Vì \[{x_1}\] và \[{x_2}\] là 2 nghiệm của phương trình \[{x^2} + x - 2 + \sqrt 2 = 0\] nên áp dụng hệ thức Vi-et ta được: \[\left\{ \begin{array}{l}{x_1} + {x_2} = - 1\\{x_1}{x_2} = - 2 + \sqrt 2 \end{array} \right.\].
Suy ra
\[x_1^3 + x_2^3\]
\[ = \left( {{x_1} + {x_2}} \right)\left( {{x_1}^2 - {x_1}{x_2} + {x_2}^2} \right) = \left( {{x_1} + {x_1}} \right)\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 3{x_1}{x_2}} \right]\]
\[ = \left( { - 1} \right){\rm{.}}\left[ {{{\left( { - 1} \right)}^2} - 3.\left( { - 2 + \sqrt 2 } \right)} \right] = 3\sqrt 2 - 7\].
Lời giải
a) \[y = \frac{1}{2}{x^2}\]
Bảng giá trị
|
\[x\] |
– 2 |
– 1 |
0 |
1 |
2 |
|
\[y\] |
2 |
\[\frac{1}{2}\] |
0 |
\[\frac{1}{2}\] |
2 |
Đồ thị hàm số \[y = \frac{1}{2}{x^2}\] là đường cong đi qua các điểm \[\left( { - 2;\,2} \right),\,\left( { - 1;\,\frac{1}{2}} \right),\,\left( {0;0} \right),\,\left( {1;\,\frac{1}{2}} \right),\,\left( {2;\,2} \right)\]
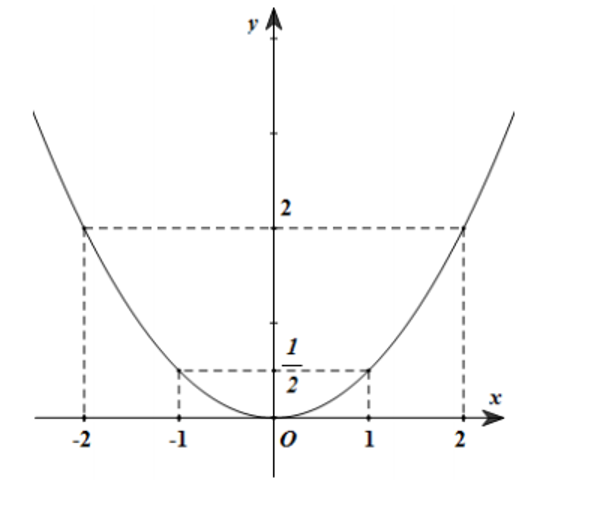
b)
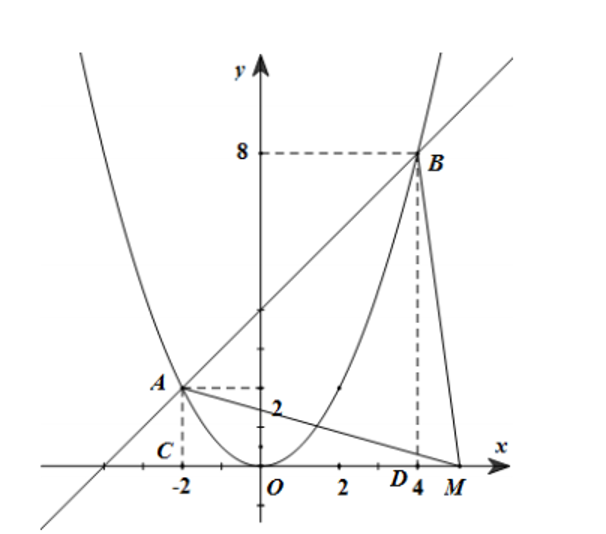
Xét phương trình hoành độ giao điểm của \[\left( P \right)\] và \[\left( d \right)\] là:
\[\frac{1}{2}{x^2} = x + 4 \Leftrightarrow {x^2} - 2x - 8 = 0\]
Ta có: \[\Delta ' = {\left( { - 1} \right)^2} - \left( { - 8} \right) = 9 > 0\]
Do đó, phương trình có 2 nghiệm phân biệt: \[x = 4;\,x = - 2\].
Với \[x = - 2\] ta có \[y = 2 \Rightarrow A\left( { - 2;\,2} \right)\]
Với \[x = 4\] ta có \[y = 8 \Rightarrow B\left( {4;\,8} \right)\].
Gọi \[M\left( {m;\,\,0} \right)\] thuộc tia \[Ox\left( {m > 0} \right)\]. Gọi \[C\left( { - 2;\,0} \right),\,D\left( {4;\,0} \right)\]. Xét hai trường hợp:
+ Trường hợp 1: \[M\] thuộc đoạn \[OD\]. Ta có \[{S_{AMB}} = {S_{ABDC}} - {S_{ACM}} - {S_{BDM}}\]
Có \[ABDC\] là hình thang có \[AC\] = 2 cm, \[BD\] = 8 cm, \[CD\] = 6 cm.
\[ \Rightarrow {S_{ABDC}} = \frac{{\left( {2 + 8} \right).6}}{2} = 30\,\,(c{m^2})\]
Suy ra \[{S_{AMB}}\] < 30 cm2 (loại).
+ Trường hợp 2: \[M\] thuộc tia \[Dx\,\,\left( {M \ne D} \right) \Rightarrow m > 4\].
Ta có :\[{S_{AMB}} = {S_{ABDC}} - {S_{ACM}} + {S_{BDM}}\]
Có \[{S_{ABDC}}\] = 30 cm2, \[MC = m + 2\] (cm), \[MD = m - 4\] (cm)
Suy ra
\[{S_{ACM}} = \frac{1}{2}AC.CM = \frac{1}{2}.2.\left( {m + 2} \right) = m + 2\,\,\,({\rm{c}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\]
\[{S_{BDM}} = \frac{1}{2}BD.DM = \frac{1}{2}.8.\left( {m - 4} \right) = 4\left( {m - 4} \right)\,\,{\rm{(c}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\]
\[ \Rightarrow {S_{AMB}} = 30c{m^2} \Leftrightarrow {S_{ACM}} = {S_{BDM}} \Leftrightarrow m + 2 = 4\left( {m - 4} \right) \Leftrightarrow m = 6\] (thỏa mãn).
Vậy \[M\left( {6;\,0} \right)\] là điểm cần tìm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.