Đề thi tuyển sinh vào lớp 10 Toán năm học 2017 - 2018 Sở GD&ĐT Hà Nội có đáp án

1)

Tính giá trị của biểu thức \[A\] khi \[x = 9\].

Với \(x = 9\)(thỏa mãn điều kiện) thay vào \[A\] ta có:

\(A = \frac{{\sqrt 9  + 2}}{{\sqrt 9  - 5}}\)\( = \frac{{3 + 2}}{{3 - 5}} =  - \frac{5}{2}\).

2)

Chứng minh \[B = \frac{1}{{\sqrt x  - 5}}\].

Với \(x \ge 0,x \ne 25\), ta có:

\(B = \frac{3}{{\sqrt x  + 5}} + \frac{{20 - 2\sqrt x }}{{x - 25}}\)

\( = \frac{{3\left( {\sqrt x  - 5} \right) + 20 - 2\sqrt x }}{{\left( {\sqrt x  + 5} \right)\left( {\sqrt x  - 5} \right)}}\)

\( = \frac{{3\sqrt x  - 15 + 20 - 2\sqrt x }}{{\left( {\sqrt x  + 5} \right)\left( {\sqrt x  - 5} \right)}}\)

\( = \frac{{\sqrt x  + 5}}{{\left( {\sqrt x  + 5} \right)\left( {\sqrt x  - 5} \right)}}\)

\( = \frac{1}{{\sqrt x  - 5}}\).

3)

Tìm tất cả giá trị của \(x\) để \[A = B.\left| {x - 4} \right|\].

Với \(x \ge 0,x \ne 25\), ta có:

\({\rm{     }}A = B.\left| {x - 4} \right|\)

\( \Leftrightarrow \frac{{\sqrt x  + 2}}{{\sqrt x  - 5}} = \frac{1}{{\sqrt x  - 5}} \cdot \left| {x - 4} \right|\)

\( \Leftrightarrow \sqrt x  + 2 = \left| {x - 4} \right|\)             (do \(x \ge 0,x \ne 25\))

\( \Leftrightarrow \sqrt x  + 2 = \left| {\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)} \right|\)

\( \Leftrightarrow 1 = \left| {\sqrt x  - 2} \right|{\rm{ }}\left( {{\rm{do }}\sqrt x  + 2 > 0} \right)\)

\( \Leftrightarrow \left[ \begin{array}{l}\sqrt x  - 2 = 1\\\sqrt x  - 2 =  - 1\end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}x = 9\\x = 1\end{array} \right.\) (thỏa mãn điều kiện)

Vậy \(x \in \left\{ {9;1} \right\}\) là giá trị cần tìm.

Một xe ô tô và một xe máy cùng khởi hành từ \(A\) để đi đến \(B\) với vận tốc của mỗi xe không đổi trên toàn bộ quảng đường \(AB\) dài \(120\,\,{\rm{km}}{\rm{.}}\) Do vận tốc xe ô tô lớn hơn vận tốc xe máy là \(10\,\,{\rm{km/h}}\) nên xe ô tô đến \(B\) sớm hơn xe máy là 36 phút. Tính vận tốc của mỗi xe.

Đổi 36 phút = \(\frac{3}{5}\) giờ.

Gọi vận tốc của xe máy là \[x\left( {{\rm{km/h}}} \right){\rm{ }}\left( {x > 0} \right)\]

Khi đó vận tốc của ô tô là \(x + 10\) (km/h).

Thời gian xe máy đi từ \(A\) đến \(B\) là \(\frac{{120}}{x}\) (giờ).

Thời gian ô tô đi từ \(A\) đến \(B\) là \(\frac{{120}}{{x + 10}}\) (giờ).

Vì xe ô tô đến \(B\) sớm hơn xe máy là 36 phút nên ta có phương trình:

\(\frac{{120}}{x} - \frac{{120}}{{x + 10}} = \frac{3}{5}\)

\( \Leftrightarrow \frac{{120x + 1200 - 120x}}{{x\left( {x + 10} \right)}} = \frac{3}{5}\)

\( \Leftrightarrow \frac{{1200}}{{{x^2} + 10x}} = \frac{3}{5}\)

\( \Leftrightarrow \frac{{400}}{{{x^2} + 10x}} = \frac{1}{5}\)

\( \Rightarrow {x^2} + 10x = 2000\)

\( \Leftrightarrow {x^2} + 10x - 2000 = 0\)

\( \Leftrightarrow \left( {x - 40} \right)\left( {x + 50} \right) = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}x = 40\left( {tm} \right)\\x =  - 50\left( {ktm} \right)\end{array} \right.\)

Vậy vận tốc của xe máy là 40 km/h; vận tốc của ô tô là \[40 + 10 = 50\] (km/h).

Giải hệ phương trình \[\left\{ {\begin{array}{*{20}{c}}{\sqrt x  + 2\sqrt {y - 1}  = 5}\\{4\sqrt x  - \sqrt {y - 1}  = 2}\end{array}} \right.\]

ĐK: \(x \ge 0,y \ge 1\)

Giải hệ phương trình:

\(\left\{ \begin{array}{l}\sqrt x  + 2\sqrt {y - 1}  = 5\\4\sqrt x  - \sqrt {y - 1}  = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\sqrt x  + 2\sqrt {y - 1}  = 5\\8\sqrt x  - 2\sqrt {y - 1}  = 4\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}9\sqrt x  = 9\\\sqrt x  + 2\sqrt {y - 1}  = 5\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}\sqrt x  = 1\\1 + 2\sqrt {y - 1}  = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\\sqrt {y - 1}  = 2\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 5\end{array} \right.\) (thỏa mãn điều kiện)

Vậy nghiệm của hệ phương trình là \[\left( {1;5} \right)\].

2a)

Chứng minh đường thẳng \(\left( d \right)\) luôn đi qua điểm \[A\left( {0;5} \right)\] với mọi giá trị của \(m.\)

Thay \[x = 0,{\rm{ }}y = 5\] vào hàm số \[y = mx + 5\], ta được:

    \(5 = m.0 + 5 \Leftrightarrow 5 = 5\) (đúng với mọi \(m\))

Vậy đường thẳng \[\left( d \right)\] luôn đi qua điểm \[A\left( {0;5} \right)\].

2b)

Tìm tất cả các giá trị của \(m\) để đường thẳng \(\left( d \right)\) cắt Parabol \[\left( P \right):y = {x^2}\] tại hai điểm phân biệt có hoành độ lần lượt là\[{x_1},{x_2}\] (với \[{x_1} < {x_2}\]) sao cho \[\left| {{x_1}} \right| > \left| {{x_2}} \right|.\]

Xét phương trình hoành độ giao điểm của \[\left( P \right)\] và \[\left( d \right)\]:

    \({x^2} = mx + 5 \Leftrightarrow {x^2} - mx - 5 = 0\)  \[\left( * \right)\]

Vì \[ac = --5 < 0\] nên phương trình \[\left( * \right)\] luôn có hai nghiệm trái dấu

\( \Rightarrow \left( d \right)\) luôn cắt \[\left( P \right)\] tại hai điểm phân biệt có hoành độ lần lượt là \[{x_1},{x_2},\] với \({x_1} < 0 < {x_2}\) (do \[{x_1},{x_2}\] trái dấu và giả sử \({x_1} < {x_2}\)).

\( \Rightarrow \left| {{x_1}} \right| =  - {x_1}\) (do \({x_1} < 0\))

\(\left| {{x_2}} \right| = {x_2}\) (do \[{x_2} > 0\])

Mà \(\left| {{x_1}} \right| > \left| {{x_2}} \right|\)

\( \Rightarrow  - {x_1} > {x_2}\)

\[ \Leftrightarrow {x_1} + {x_2} < 0\]

\[ \Leftrightarrow m < 0\] (theo hệ thức Vi-ét)

Vậy \(m < 0\) là giá trị cần tìm.

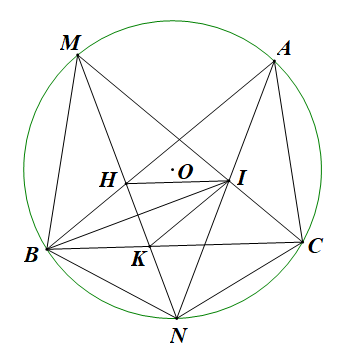
1)

Chứng minh bốn điểm \[C,N,K,I\] cùng thuộc một đường tròn.

Ta có \(\widehat {MNA},\widehat {MCB}\) là các góc nội tiếp chắn lần lượt các cung nhỏ \[MA,MB\]

Mà  (do \(M\) là điểm chính giữa của )

\( \Rightarrow \widehat {MNA} = \widehat {MCB}\)

Hay \(\widehat {KNI} = \widehat {KCI}\), mà hai góc này cùng nhìn đoạn \(KI\)

Þ Tứ giác \(CNKI\) nội tiếp đường tròn.

Þ Bốn điểm \[C,N,K,I\] cùng thuộc một đường tròn.

2)

Chứng minh \[N{B^2} = NK.NM\].

Ta có \(\widehat {NBC},\widehat {NMB}\) là các góc nội tiếp chắn lần lượt các cung nhỏ \[NC,NB\]

Mà  (do \(N\) là điểm chính giữa của )

\[ \Rightarrow \widehat {NBC} = \widehat {NMB}\]

Hay \[\widehat {NBK} = \widehat {NMB}\].

Xét \(\Delta NBK\) và \(\Delta NMB\) có:

\(\widehat {BNM}\) là góc chung; \[\widehat {NBK} = \widehat {NMB}\] (chứng minh trên)

\( \Rightarrow \frac{{NB}}{{NM}} = \frac{{NK}}{{NB}}\) (tỉ số đồng dạng)

\( \Rightarrow N{B^2} = NK.NM\).

3)

Chứng minh tứ giác \[BHIK\]là hình thoi.

Vì tứ giác \[CNKI\] nội tiếp nên \(\widehat {INC} = \widehat {IKC}\) (hai góc nội tiếp cùng chắn cung \[CI\])

Mà \(\widehat {INC} = \widehat {ANC} = \widehat {ABC}\) (hai góc nội tiếp cùng chắn cung \[AC\] của \[\left( O \right)\])

\( \Rightarrow \widehat {IKC} = \widehat {ABC}\)

Lại có hai góc này ở vị trí đồng vị nên \[KI\,{\rm{//}}\,BH\].

Chứng minh tương tự ta được \[HI\,{\rm{//}}\,BK\].

Tứ giác \[BHIK\] có các cạnh đối song song nên là hình bình hành.

Cách 1:

Vì  nên \(\widehat {ACM} = \widehat {BCM}\), hay \[CM\] là tia phân giác của \(\widehat {ACB}\)

Tương tự, \[AN\] là tia phân giác của góc \[\widehat {BAC}\]

\[\Delta ABC\] có hai đường phân giác \[AN\] và \[CM\] cắt nhau tại \(I\)

\( \Rightarrow BI\) là đường phân giác thứ ba của \[\Delta ABC\]

Hình bình hành \[BHIK\] có \[BI\] là đường phân giác của góc \(B\) nên là hình thoi.

Cách 2:

Vì \(\widehat {BHN},\widehat {BKH}\) là các góc có đỉnh ở bên trong đường tròn \(\left( O \right)\) nên:

 và

\( \Rightarrow \widehat {BHN}{\rm{ = }}\widehat {BKH}\) (do  và )

\( \Rightarrow \Delta BHK\) cân tại \(B\) \[ \Rightarrow BH = BK\]

Hình bình hành \[BHIK\] có \[BH = BK\] nên là hình thoi.

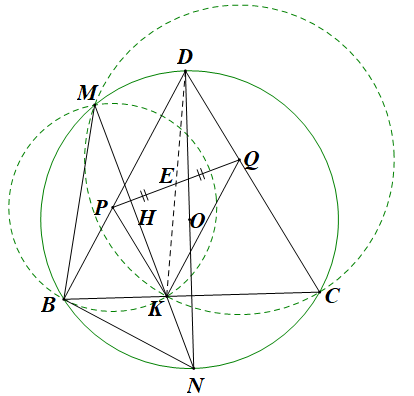
4)

Gọi \(P,Q\) lần lượt là tâm của các đường tròn ngoại tiếp tam giác \[MBK\], tam giác \[MCK\] và \[E\] là trung điểm của đoạn \[PQ\]. Vẽ đường kính \[ND\] của đường tròn \[\left( O \right)\]. Chứng minh ba điểm \[D,E,K\] thẳng hàng.

Cách 1:

\[\left( P \right)\] có góc \(\widehat {BMN}\) là góc nội tiếp, góc \(\widehat {BPK}\) là góc ở tâm cùng chắn

\( \Rightarrow \widehat {BMN} = \frac{1}{2}\widehat {BPK}\)

Mà \(\Delta PBK\) cân tại \(P\) (vì \[PB = PK\])

\( \Rightarrow \widehat {PBK} = \frac{{180^\circ  - \widehat {BPK}}}{2} = 90^\circ  - \frac{1}{2}\widehat {BPK} = 90^\circ  - \widehat {BMK}\) \[\left( 1 \right)\]

\[\left( O \right)\] có đường kính \(ND\) đi qua \(N\) là điểm chính giữa của cung \[BC\]

\( \Rightarrow ND \bot BC\) và \(ND\) đi qua trung điểm của \[BC\]

\( \Rightarrow \Delta DBC\) cân tại \(D\)

\( \Rightarrow \widehat {DBC} = \frac{{180^\circ  - \widehat {BDC}}}{2} = 90^\circ  - \frac{1}{2}\widehat {BDC}\)

Trong \[\left( O \right)\], \(\widehat {BMK} = \widehat {BDN} = \frac{1}{2}\widehat {BDC}\)

\( \Rightarrow \widehat {DBC} = 90^\circ  - \widehat {BMK}\) \[\left( 2 \right)\]

Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] \( \Rightarrow \widehat {PBK} = \widehat {DBC}\)

Þ Ba điểm \[D,P,B\] thẳng hàng

Lại có \(\widehat {BPK} = \widehat {BDC}{\rm{ }}\left( { = 2\widehat {BMK}} \right)\) và hai góc ở vị trí đồng vị

\( \Rightarrow PK\,{\rm{//}}\,DC\)

Chứng minh tương tự được ba điểm \[D,Q,C\] thẳng hàng và \[QK\,{\rm{//}}\,DB\]

Do đó, \(PK\,{\rm{//}}\,DC\) và \[QK\,{\rm{//}}\,DB\]

Tứ giác \[DPKQ\] là hình bình hành

Do đó \(E\) là trung điểm của đường chéo \[PQ\] thì \(E\) cũng là trung điểm của đường chéo \(DK\).

Vậy ba điểm \[D,E,K\] thẳng hàng.

Có thể chứng minh ba điểm \[D,P,B\] thẳng hàng theo các cách sau:

Cách 2:

\[\left( P \right)\] có góc \(\widehat {BMN}\) là góc nội tiếp, góc \(\widehat {BPK}\) là góc ở tâm cùng chắn

\( \Rightarrow \widehat {BMN} = \frac{1}{2}\widehat {BPK}\)

Mà \(\Delta PBK\) cân tại \(P\) (vì \[PB = PK\])

\( \Rightarrow \widehat {PBK} = \frac{{180^\circ  - \widehat {BPK}}}{2} = 90^\circ  - \frac{1}{2}\widehat {BPK} = 90^\circ  - \widehat {BMK}\) \[\left( 1 \right)\]

\( \Rightarrow \widehat {PBK} + \widehat {BMK} = 90^\circ \)

\[\left( O \right)\] có đường kính \(ND\) đi qua \(N\) là điểm chính giữa của cung \[BC\]

\( \Rightarrow ND \bot BC\) \( \Rightarrow \widehat {DBK} + \widehat {BDN} = 90^\circ \)

\( \Rightarrow \widehat {DBK} + \widehat {BMK} = 90^\circ \) (do \(\widehat {BDN} = \widehat {BMK}\))

Lại có \(\widehat {PBK} + \widehat {BMK} = 90^\circ \) (chứng minh trên)

\( \Rightarrow \widehat {PBK} = \widehat {DBK} \Rightarrow \) ba điểm \[D,P,B\] thẳng hàng.

Cách 3:

\[\left( P \right)\] có \(\widehat {BMK}\)  là góc nội tiếp nên

Mà \[\widehat {BMK} = \widehat {CBN}\] nên

Suy ra \[BN\] là tiếp tuyến tại \(B\) của \[\left( P \right)\]

\( \Rightarrow BN \bot PB\)

Lại có \(\widehat {DBN} = 90^\circ \) (góc nội tiếp chắn nửa \(\left( O \right)\))

\( \Rightarrow BN \bot DB\)

Do đó ba điểm \[D,P,B\] thẳng hàng.