Đề thi minh họa Toán vào 10 năm học 2025 - 2026 TP Hồ Chí Minh
123 người thi tuần này 4.6 4.4 K lượt thi 7 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
1) Vẽ đồ thị \[\left( P \right)\] của hàm số \(y = \frac{{{x^2}}}{2}.\)
Ta có bảng giá trị:
|
x |
\[ - 4\] |
\[ - 2\] |
0 |
2 |
4 |
|
\(y = \frac{{{x^2}}}{2}\) |
8 |
2 |
0 |
2 |
8 |
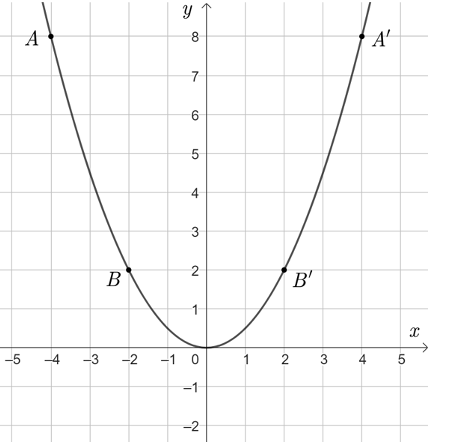
Trên mặt phẳng tọa độ, lấy các điểm \[A\left( { - 4\,;\,\,8} \right)\,;\,\,B\left( { - 2\,;\,\,2} \right)\,;\,\,O\left( {0\,;\,\,0} \right)\,;\,\,A'\left( {4\,;\,\,8} \right)\,;\,\,\]
\[B\;'\left( {2\,;\,\,2} \right).\]
Đồ thị hàm số \(y = \frac{{{x^2}}}{2}\) là một đường parabol đỉnh \[O,\] đi qua các điểm trên và có dạng như dưới đây.
2) Điểm có tung độ và hoành độ bằng nhau nên gọi \[M\left( {{x_0};\,\,{x_0}} \right)\] thì \[{x_0} = \frac{{x_0^2}}{2}\]
Suy ra \[x_0^2 = 2{x_0}\] hay \[x_0^2 - 2{x_0} = 0\]
\[{x_0}\left( {{x_0} - 2} \right) = 0\]
\[{x_0} = 0\] hoặc \[{x_0} - 2 = 0\]
Vậy những điểm \[M\] thuộc \[\left( P \right)\] có tung độ và hoành độ bằng nhau là \[M\left( {0\,;\,\,0} \right)\] và \[M\left( {2\,;\,\,2} \right).\]
Lời giải
1) Phương trình \[2{x^2} - 5x + 1 = 0\] có \[a = 2\,;\,\,b = - 5\,;\,\,c = 1\] nên ta có:
\[\Delta \; = \;{\left( { - 5} \right)^2} - \;4 \cdot 2 \cdot 1 = \;25 - \;8 = \;17 > \;0\] nên phương trình có hai nghiệm phân biệt.
2) Áp dụng định lí Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{5}{2}\\{x_1}{x_2} = \frac{1}{2}\end{array} \right.\).
Ta có: \[A = {x_1}\left( {{x_1} + 2024} \right) + {x_2}\left( {{x_2} + 2025} \right) - {x_2}\]
\[ = x_1^2 + 2024{x_1} + x_2^2 + 2025{x_2} - {x_2}\]
\[ = x_1^2 + 2024{x_1} + x_2^2 + 2024{x_2}\]
\[ = \left( {x_1^2 + 2{x_1}{x_2} + x_2^2} \right) - 2{x_1}{x_2} + \left( {2024{x_1} + 2024{x_2}} \right)\]
\[ = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} + 2024\left( {{x_1} + {x_2}} \right)\]
\[ = {\left( {\frac{5}{2}} \right)^2} - 2 \cdot \frac{1}{2} + 2024 \cdot \frac{5}{2}\]
\[ = \frac{{25}}{4} - 1 + 5060 = \frac{{20\,\,261}}{4}\].
Vậy \[A = \frac{{20\,\,261}}{4}\].
Lời giải
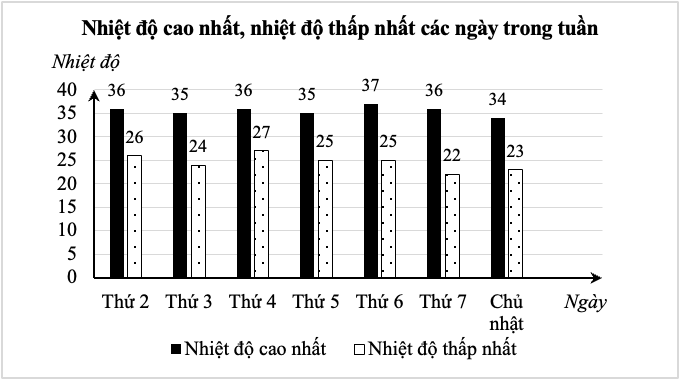
1) Dựa vào biểu đồ cột kép, ta có biên độ nhiệt của các ngày trong tuần là:
Thứ 2: \[36 - 26 = 10,\] thứ 3: \[35 - 24 = 11,\] thứ 4: \[36 - 27 = 9;\] thứ 5: \[35 - 25 = 10;\]
Thứ 6: \[37 - 25 = 12;\] thứ 7: \[36 - 22 = 14;\] chủ nhật: \[34 - 23 = 11.\]
Vậy ngày có biên độ nhiệt lớn nhất trong tuần của thành phố Hồ Chí Minh là thứ 7.
2) Ta có số ngày có nhiệt độ cao không quá 35 độ C là 3 (ngày).
Suy ra số phần tử của biến cố A là 3.
Xác suất để ngày được chọn có nhiệt độ cao nhất không quá 35 độ C là \(\frac{3}{7}\).
Có số ngày có biên độ nhiệt nhỏ hơn 12 độ C là 5 (ngày).
Suy ra số phần tử của biến cố B là 5.
Xác suất để ngày được chọn có biên độ nhiệt nhỏ hơn 12 độ C là \(\frac{5}{7}.\)
Lời giải
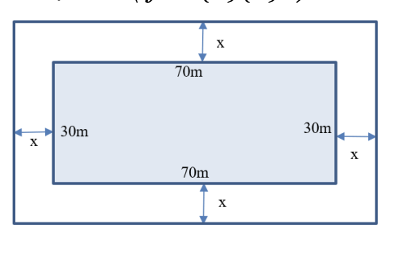
1) Chiều rộng của khu vườn hình chữ nhật sau khi mở rộng là:
\[30 + x + x = 30 + 2x\,\,\left( {\rm{m}} \right)\]
Chiều dài của khu vườn hình chữ nhật sau khi mở rộng là:
\[70 + x + x = 70 + 2x\,\,\left( {\rm{m}} \right)\]
Diện tích của khu vườn hình chữ nhật sau khi mở rộng là:
\[\left( {30 + 2x} \right)\left( {70 + 2x} \right)\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\]
Vậy biểu thức \[S\] biểu diễn theo \[x\] là \[S = \left( {30 + 2x} \right)\left( {70 + 2x} \right)\].
2) Điều kiện: \[x > 0\].
Diện tích của khu vườn ban đầu là: \[70 \cdot 30{\rm{ }} = 2\,\,100\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\]
Vì sau khi mở rộng thì diện tích của khu vườn lớn hơn diện tích ban đầu \[1\,\,150\,\,{{\rm{m}}^{\rm{2}}}\] nên phương trình:
\[\left( {30 + 2x} \right)\left( {70 + 2x} \right) = 2\,\,100 + 1\,\,150 = 3\,\,250\]
\[2100 + 60x + 140x + 4{x^2} = 3\,\,250\]
\[4{x^2} + 200x - 1\,\,150 = 0\]
\[2{x^2} + 100x - 575 = 0\]
Ta có \[\Delta '\; = 3\,\,650 > 0\;\] nên phương trình có hai nghiệm phân biệt:
\[{x_1} \approx 5,2\] (thỏa mãn) hoặc \[{x_2} \approx - 55,2\] (không thỏa mãn).
Vậy giá trị của \[x\] là khoảng \[5,2\,\,{\rm{m}}.\]
Lời giải
1) Bán kính của phần ruột quả dưa hấu là: \(\frac{{25 - 2 \cdot 2}}{2} = 10,5\,\,\left( {{\rm{cm}}} \right).\)
Thể tích phần ruột của quả dưa hấu là: \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi \cdot {10,5^3} \approx 4\,\,849,05\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)
Vậy thể tích phần ruột của quả dưa hấu khoảng \(4\,\,849,05\,\,{\rm{c}}{{\rm{m}}^3}.\)
2) Thể tích nước ép dưa hấu là: \[{V_n} = \;80\% \cdot 4\,\,849,05 = \;3\,\,879,24\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\]
Thể tích của phần đựng nước ly thuỷ tinh là:
\[{V_l} = 70\% \cdot \pi {R^2}h = 70\% \cdot \pi \cdot {\left( {\frac{5}{2}} \right)^2} \cdot 10 \approx 137,44\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\]
Ta có \[\frac{{{V_n}}}{{{V_l}}} \approx \frac{{\;3\,\,879,24}}{{137,44}} \approx 28,22\].
Do đó cần ít nhất 29 cái ly để đựng hết nước ép của quả dưa hấu.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Một quả dưa hấu không hạt ruột đỏ dạng hình cầu có đường kính 25cm và phần vỏ dày 2 cm] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/anh-man-hinh-2025-10-24-luc-200412-1761310950.png)